Стабилизация трехмассовой системы: модальный метод синтеза в пространстве состояний с наблюдателем пониженного порядка

Новосибирск, 2012

Цель работы

Исследование двухканальной системы, состоящей из трех масс, с помощью модального метода синтеза с наблюдателем пониженного порядка.

Исходные данные

Таблица 1.

Ход работы

Модель объекта

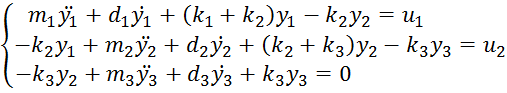
Найдем описание объекта в пространстве состояний, для чего вторые производные оставим слева, перейдем к изображениям, разделим на s2 и сгруппируем члены по степеням s:

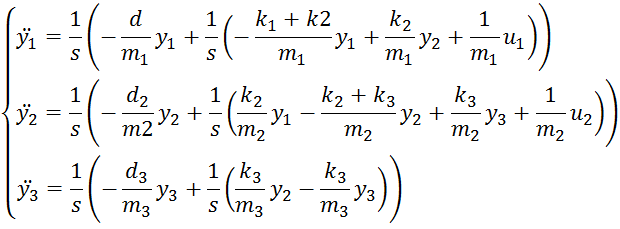
Каждое уравнение можно представить в виде двух интеграторов, соединенных слева направо: обозначим выход правого интегратора первого уравнения через x1 , что соответствует содержимому внешней скобки, и через x2 выход первого интегратора, что соответствует содержимому внутренней скобки. Аналогичные обозначения введем для второго и третьего уравнений. При данных обозначениях оказывается, что y1=x1 и y2=x3.

Описание объекта в пространстве состояний следующее:

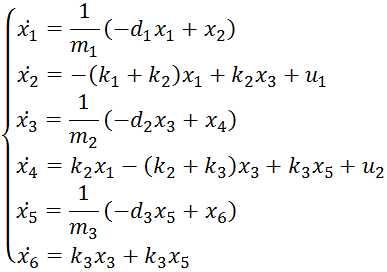
Составим матрицы при заданных значениях параметров:

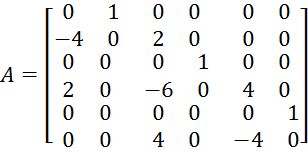
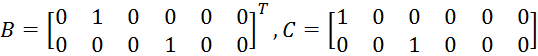
Обеспечить в системе собственные числа {-1 -1 -1 -1 -1 -1}

Расчет наблюдателя пониженного порядка

Рассчитаем наблюдатель пониженного порядка, используя стандартную процедуру.

Уравнение наблюдателя:

Для расчета матриц T, G₂, G, H зададим матрицы F и G₁. Матрица F задается из условий быстродействия:

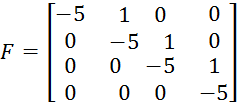
Матрица G₁ задается из условия управляемости по каналу y:

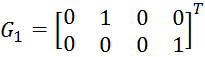
С помощью пакета MATLAB рассчитаны матрицы T, G₂, G и H.

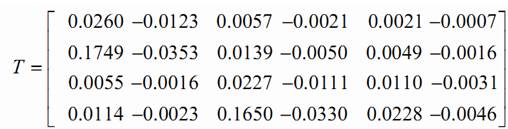
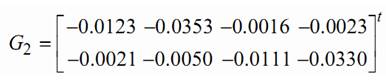
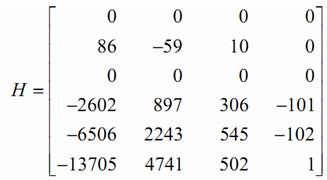
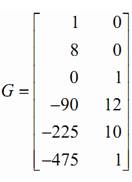
Вычисление матрицы обратной связи

С помощью пакета MATLAB нашли описание объекта в управляемой канонической форме и матрицу обратной связи:

 

 

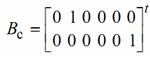
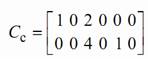
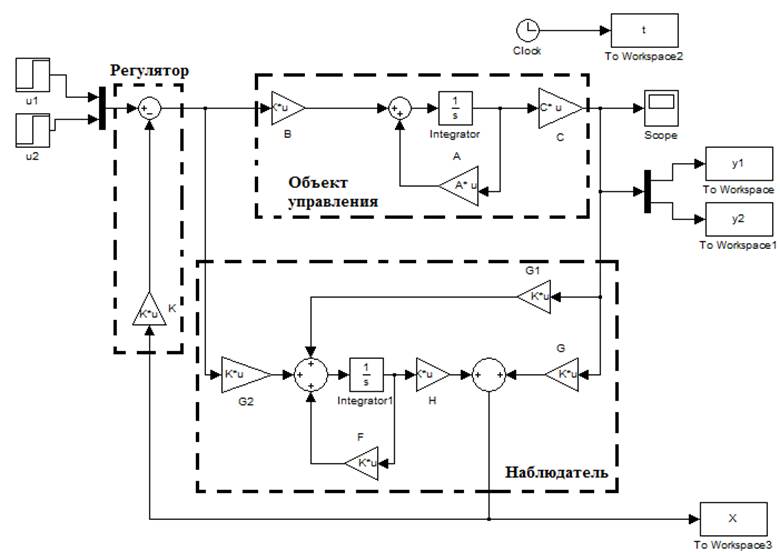
Рис.1 Схема системы управления с регулятором и наблюдателем пониженного порядка.

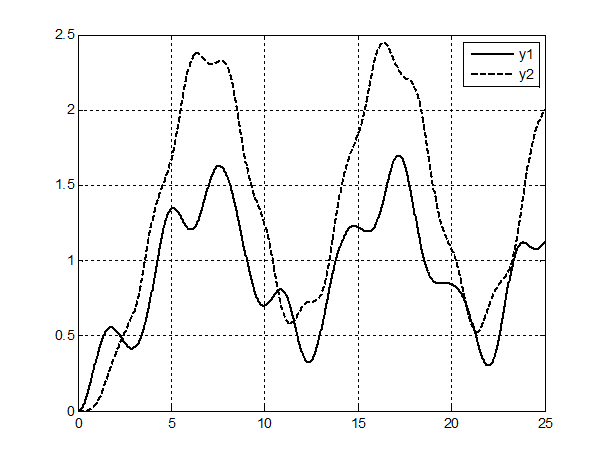
Рис.2 Переходные процессы у₁ и y₂ в системе без регулятора и наблюдателя

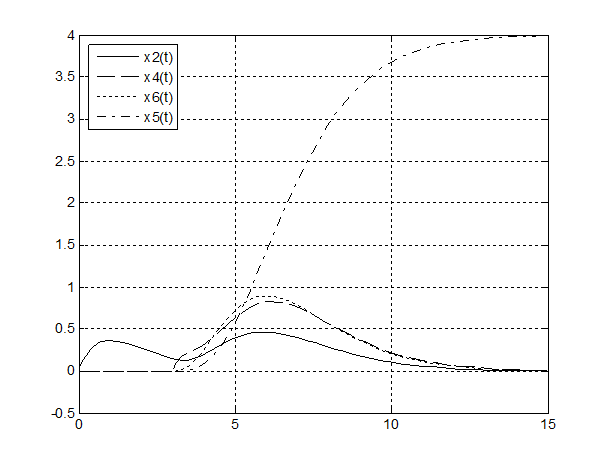
Рис.3 Переменные состояния на выходе наблюдателя (искл. x₁ и x₃, т.к. y₁=x₁, y₂=x₂)

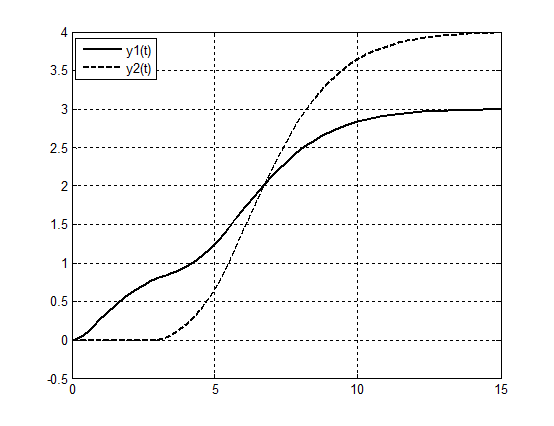
Рис.4 Работа схемы с регулятором и наблюдателем y₁ и y₂

Выводы

В ходе лабораторной работы была решена задача модального синтеза многоканального регулятора (наблюдателя пониженного порядка и обратной связи с матрицей коэффициентов) в пространстве состояний на примере двухканальной системы, состоящей из трех масс. В данном случае «сложность» регулятора, которую можно оценить как размер матрицы F, меньше размера матрицы объекта A на число «выходов» объекта. Статический режим при таком методе синтеза неудовлетворителен.

Приложение

Листинг MATLAB*

G1=[0 0; 1 0; 0 0 ; 0 1];

F=[-5 1 0 0; 0 -5 1 0; 0 0 -5 1; 0 0 0 -5];

A=[0 1 0 0 0 0; -4 0 2 0 0 0; 0 0 0 1 0 0 ; 2 0 -6 0 4 0; 0 0 0 0 0 1; 0 0 4 0 -4 0];

B=[0 1 0 0 0 0; 0 0 0 1 0 0]';

C=[1 0 0 0 0 0; 0 0 1 0 0 0];

G1C=G1*C;

E6=eye(6);

E4=eye(4);

W1=kron(F,E6);

W2=kron(E4,A');

W=-W1 + W2;

g1c=reshape(G1C',24,1);

t=W\g1c;

T=reshape(t,6,4)';

G2=T*B;

Q=[T;C];

X=Q^-1;

H=X(:,1:4);

C=X(:,5:6);

U=[B,A*B,A^2*B,A^3*B,A^4*B,A^5*B];

B;

b1=B(:,1)';

b2=B(:,2)';

U1=[b1,A*b1,b2,A*b2,A^2*b2, A^3*b2];

R=U1^-1;

R;

q1=R(2,:);

q2=R(6,:);

P=[q1' (q1*A)' q2' (q2*A)' (q2*A^2)' (q2*A^3)']';

Ac=P*A*P^-1;

Bc=P*B;

Cc=[1 0 0 0 0 0; 0 0 1 0 0 0]*P^-1; % С первоначальная нужна

Ac=Ac';

Ob=[Ac(:,2) Ac(:,6)]';

Ac=Ac';

J=[-1 -2 0 0 0 0; 2 0 -1 -4 -6 -4];

Kc=Ob-J;

Kc.

* Жирным шрифтом помечены формулы, в написание которых были внесены изменения для обеспечения должного функционирования по сравнению с методическим пособием СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. – 2010. – № 4(62). – 13–24