Стабилизация двухмассовой системы: модальный метод синтеза с использованием полиномиального разложения

Министерство образования и науки РФ

Федеральное агентство по образованию

Новосибирский государственный технический университет

Кафедра Автоматики

Лабораторная работа №1

Стабилизация двухмассовой системы:
модальный метод синтеза с использованием
полиномиального разложения

Факультет: АВТ  

Группа: ААМ–10

Студенты: Розенталь П.                                                 Преподаватель:

          Ливенец Д.                                                  Воевода А.А.      

                    Малинников А.                                                    

Новосибирск, 2010

Цель работы

Разработать и синтезировать регулятор для двухканальной системы, обеспечить астатический режим.

Выполнение работы

Модель объекта представляет собой систему из двух грузов, подвешенных последовательно на двух пружинах жесткости  и  с коэффициентами демпфирования  и . Предполагается два управляющих сигнала – силы –  и , приложенные к массам  и .

Управляемые величины – координаты грузов  и , отсчитываемые от состояния равновесия. Выпишем модель объекта управления:

,

.

Таблица 1. Исходные данные

При отсутствии демпфирования(=0 и =0) модель объекта «вход - выход» следующая:

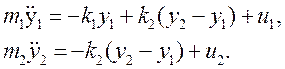                                         (1)

Перейдём к описанию в пространстве состояний. Запишем наблюдаемую каноническую форму:

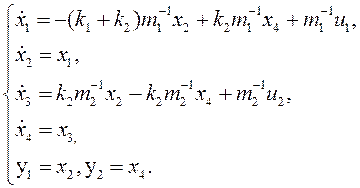                      (2)                 

С учётом исходных данных уравнение (2) примет вид:,  ,  .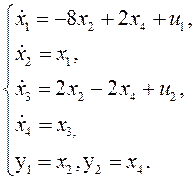

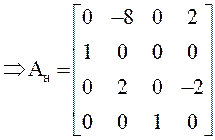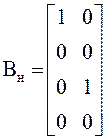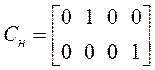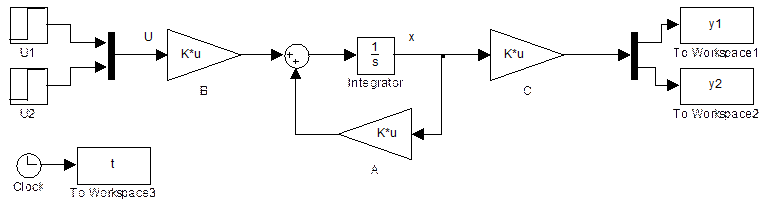
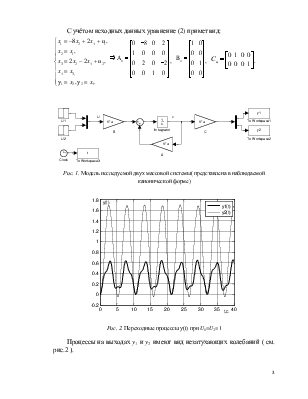
Рис. 1. Модель исследуемой двух массовой системы( представлена в наблюдаемой канонической форме)

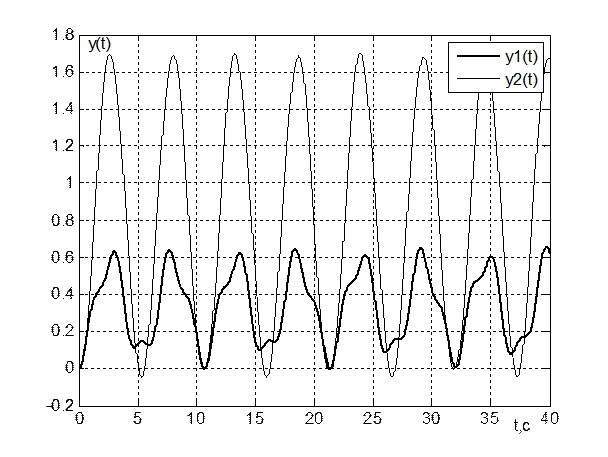
Рис. 2. Переходные процессы y(t) при U₁=U₂=1

Процессы на выходах y₁ и y₂ имеют вид незатухающих колебаний ( см. рис.2 ).

Поставим задачу автономизации каналов с заданными полюсами у замкнутой системы. В качестве исполнительных органов используем интеграторы.

С учетом интеграторов

система (1) примет вид:

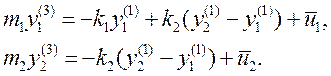
          Перейдем к полиномиальному описанию:

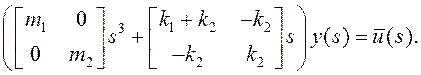
Здесь и .

С учётом исходных данных запишем:

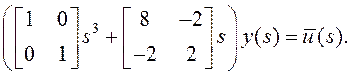
Обозначим матрицы при  и  через  и  и :

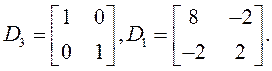
Выберем структуру системы управления вида «задание – сигнал рассогласования – регулятор – объект – обратная связь». Опишем систему уравнениями:

,   ,  

Передаточная функция системы имеет вид:

                                         .                                       (3)           

          Выберем правое разложение для объекта и левое разложение для регулятора, т.е.

            ,  .                            (4)                     

          Найдем связь между входом  и выходом. Подставив (4) в (3), получим:

.

                                                                                   (5)       

          Здесь C(s) ­– желаемая характеристическая матрица системы размером 2 на 2.

,    .                      

     Для регулятора выберем полиномиальные матрицы числителя и знаменателя степени два:

                                  , .                    (6)

Тогда степень матрицы C(s) должна быть равна пяти. Зададим . Получим:

                           .                   (7)

          После подстановки  (6,7) в (5) примет вид:

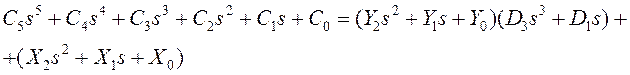
Приравняем коэффициенты при одинаковых степенях :

,, , , ,

          Найдём неизвестные:

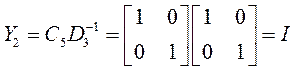
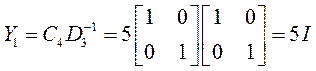
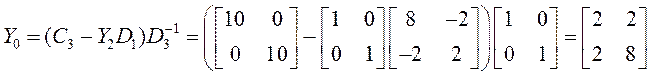
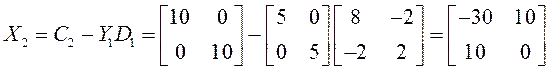
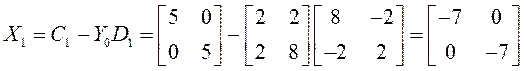
          Выражение для управления имеет вид:

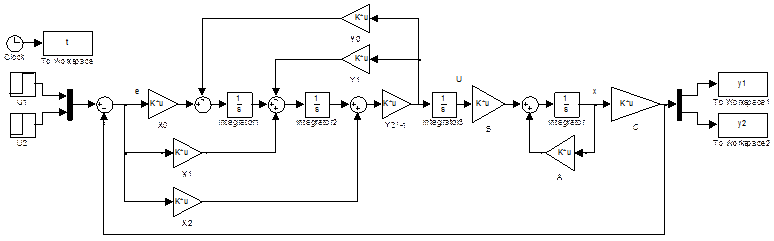
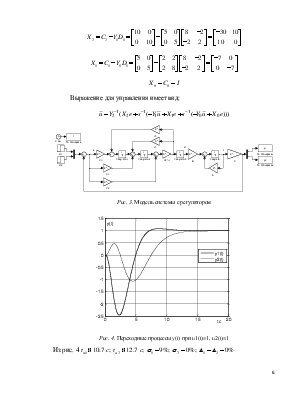
Рис. 3. Модель системы с регулятором

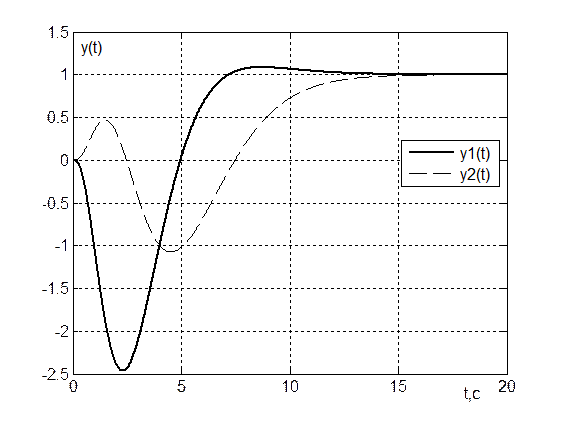
Рис. 4. Переходные процессы y(t) при u1(t)=1, u2(t)=1

Из рис. 4

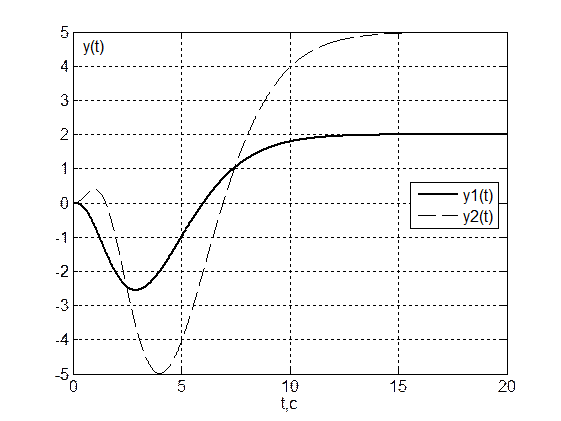
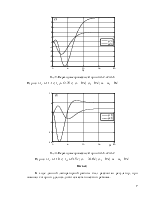
Рис. 5. Переходные процессы y(t) при u1(t)=2, u2(t)=5

Из рис. 4

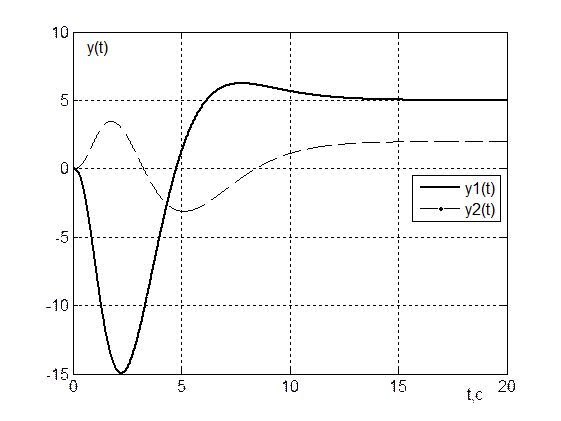
Рис. 6. Переходные процессы y(t) при u1(t)=5, u2(t)=2

Из рис. 4

Вывод

В ходе данной лабораторной работы был рассчитан регулятор, при помощи которого удалось добиться астатического режима.