Решение линейных обыкновенных дифференциальных уравнений алгоритмами Рунге-Кутта и Адамса четвертого порядка точности

2. Основные теоретические положения

            Из численных методов решения линейных обыкновенных дифференциальных уравнений чаще всего на практике используют алгоритмы Рунге-Кутта и Адамса четвертого порядка точности с прогнозом и коррекцией решения.

            Пусть необходимо отыскать решение дифференциального уравнения вида

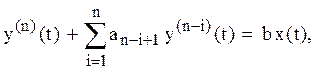
                                                        (2.1)

     Учитывая, что  где  - шаг дискретизации по времени, а  выражение (2.1) запишем в виде

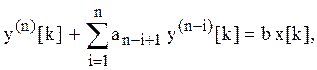
                                     (2.2)

   Численная реализация метода Рунге-Кутта четвертого порядка точности:

1)  для -го момента времени определяются коэффициенты   

                       …

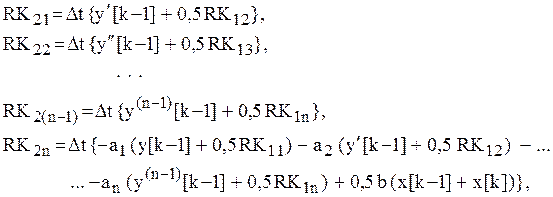
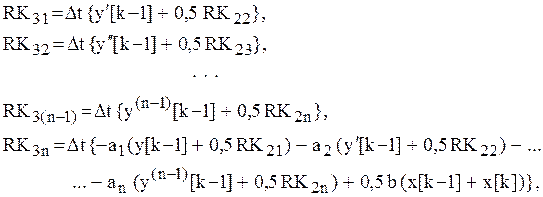
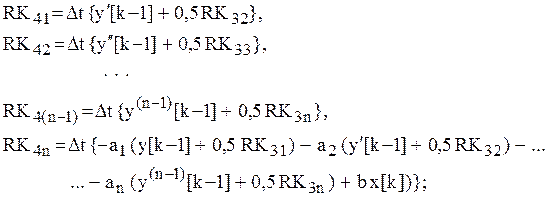
2) для -го момента времени определяются решение и его производные

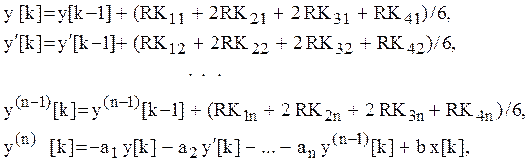
при   

Описанный алгоритм реализован в подпрограмме N1YRKC (см. приложение).

Численная реализация метода Адамса четвертого порядка точности с прогнозом и коррекцией решения:

1) для -го момента времени явным методом Адамса третьего порядка точности вычисляется прогноз решения и его производных

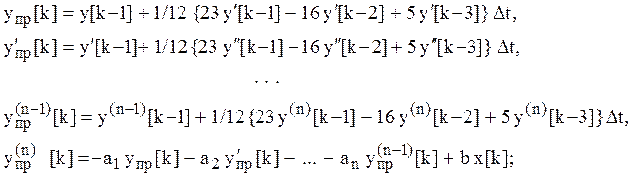
2) для -го момента времени неявным методом Адамса третьего порядка точности производится  коррекция решения и его производных

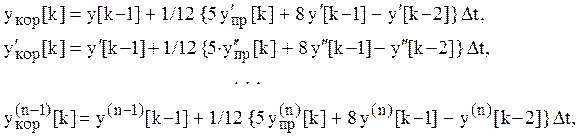
3)  для -го момента времени определяется решение и его производные

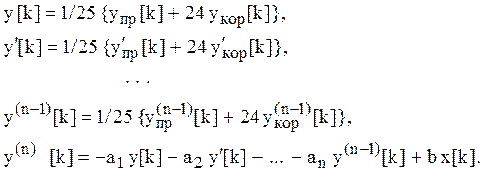
Последняя операция позволяет повысить порядок точности описанного комбинационного алгоритма на единицу, поскольку при суммировании погрешности явного и неявного алгоритмов, имеющие противоположные знаки, частично приводятся.