МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Расчетно-графическая работа №2
по дисциплине «МСЗИ»
Вариант 18
|
Факультет: АВТ Группа: АА-86 Студент: Земцов Н.С. |
Преподаватель: Каменский С.В. Дата: 05.05.11 |
Новосибирск
2011
Задание:
|
18 |
M |
n |
k |
d |
D |
№ сообщения |
p18(x)=x3+x+1 |
|||||||
|
2-10 7-3-2-1 |
? |
? |
8 |
? |
? |
39 |
||||||||
|
2-8 |
? |
? |
6 |
? |
? |
49 |
||||||||
|
КПВ |
200 |
? |
? |
? |
? |
25 |
||||||||
|
МКХ |
? |
? |
8 |
? |
? |
180 |
? |
? |
- |
- |
- |
- |
x5 |
? |
|
ЦК |
14 |
? |
? |
? |
? |
11 |
? |
? |
- |
- |
p18(x) |
? |
x4 |
? |
|
M |
n |
k |
d |
D |
№ сообщения |
r |
s |
P |
H |
p(x) |
h(x) |
E(x) |
S(x) |
|
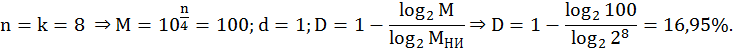
Закодируем 39 двоично-десятичным кодом с весами 7-3-2-1:
![]()

Закодируем 49 двоично-восьмеричным кодом:
![]()
Для обеспечения ![]() необходимо как минимум
необходимо как минимум ![]() Наибольшая мощность при
Наибольшая мощность при ![]() , где
, где ![]() – число единиц.
– число единиц.

Для кодов с постоянным весом соответствие номера сообщения и кодовой комбинации задается с помощью таблицы, предположим, что сообщение 25 кодируется комбинацией 1010101010.
![]()
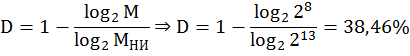
Запишем представление сообщения в классическом КХ:
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12, где a1, a2, a4, a8 – контрольные символы, а остальные – информационные.
Запишем уравнения проверок по известному правилу (“с первого по одному через один”, “со второго по два через два и т.д.”):

В МКХ добавляется еще один контрольный символ общей проверки на четность (a13), запишем для него уравнение проверок:
![]()
Разрешим уравнения относительно контрольных символов:
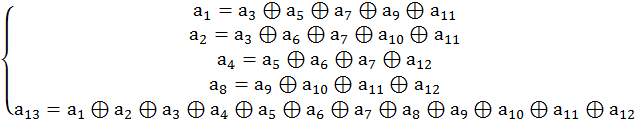
Закодируем 180:
![]()
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
a13 |
|
_ |
_ |
1 |
_ |
0 |
1 |
1 |
_ |
0 |
1 |
0 |
0 |
_ |
Рассчитаем контрольные символы:
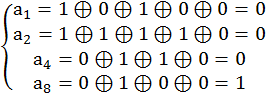
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
a13 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
_ |
![]()
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
a13 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
Декодирование: ![]() , следовательно, было принято:
, следовательно, было принято:
|
a1 |
a2 |
a3 |
a4 |
a5 |
a6 |
a7 |
a8 |
a9 |
a10 |
a11 |
a12 |
a13 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
Рассчитаем синдром Хэмминга и синдром ОПЧ:
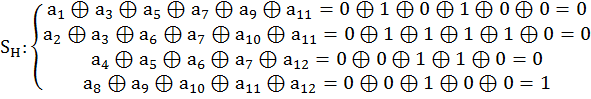
![]()
![]()
Т.к. ![]() и
и ![]() => ошибка одиночная, коррекция
проводится по синдрому Хэмминга:
=> ошибка одиночная, коррекция
проводится по синдрому Хэмминга:
![]() ошибка в a8.
ошибка в a8.
![]()
![]()
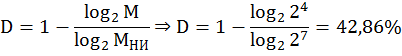
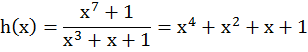
Закодируем ![]() делением на полином p(x):
делением на полином p(x):
![]()
![]() , где
, где ![]()
![]()
Декодирование:
![]()
Неселектируемый синдром:
![]()
Селектриуемый синдром:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.