Положения равновесия и устойчивость нелинейных систем

Министерство образования РФ

Новосибирский Государственный Технический Университет

Кафедра Автоматики

Лабораторная работа №2

Положения равновесия и устойчивость нелинейных систем

Факультет:   АВТ                                                               Проверила:  Шпилевая О.Я.

Группа:        АА-124

Бригада:      2

Выполнили: Орсоев А.В.,

                    Перевалов Д.Ц.,

                    Гатенюк А.О.

Новосибирск, 2004

Цель работы:

          Исследовать устойчивость систем с однозначными и неоднозначными нелинейными  характеристиками относительно положений равновесия.

Исходные данные:

Дифференциальные уравнения:

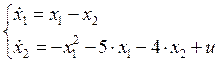
u=4, a₀=0.41, a₁=1

1. Найдем точки равновесия при u=0:

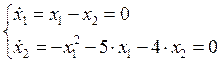
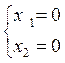    или

2. Выясним, устойчивы ли эти положения равновесия:

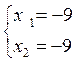
X[0;0]^T

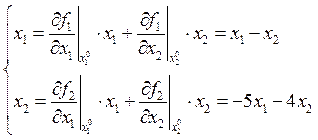
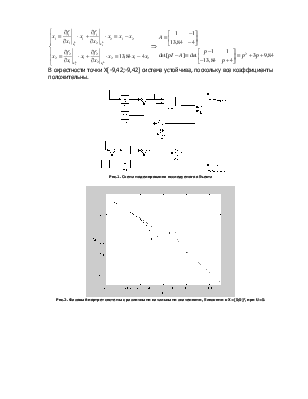
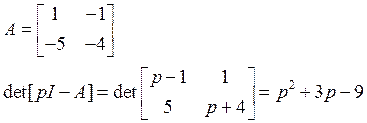
В окрестности данной точки система неустойчива, поскольку не все коэффициенты при p положительны.

X[-9;-9]^T

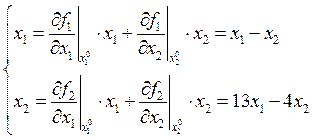
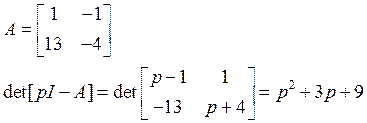
В окрестности точки X[-9;-9] система устойчива, поскольку все коэффициенты положительны.

3. Найдем точки равновесия при u=4:

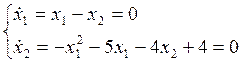
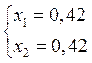 или

4. Выясним, устойчивы ли эти положения равновесия:

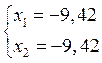
X[0,42;0,42]^T

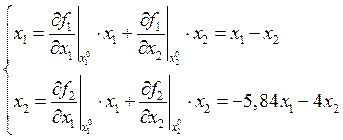
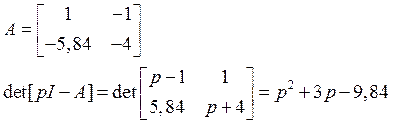
В окрестности данной точки система неустойчива, поскольку не все коэффициенты при p положительны.

X[-9,42;-9,42]^T

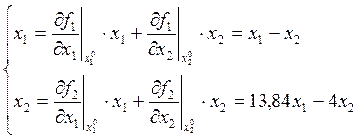
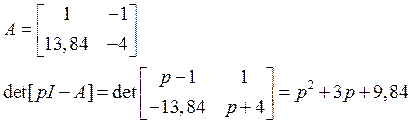
В окрестности точки X[-9,42;-9,42] система устойчива, поскольку все коэффициенты положительны.

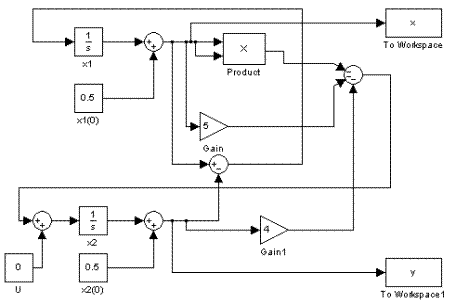
Рис.1. Схема моделирования исследуемого объекта

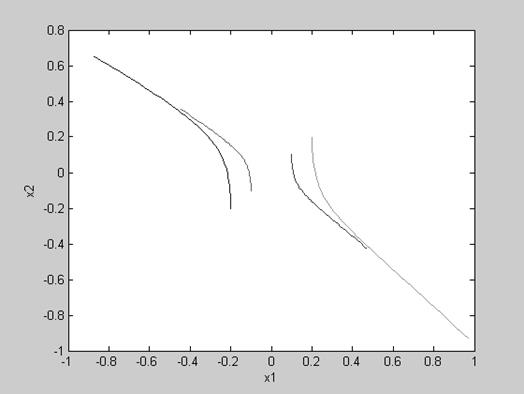
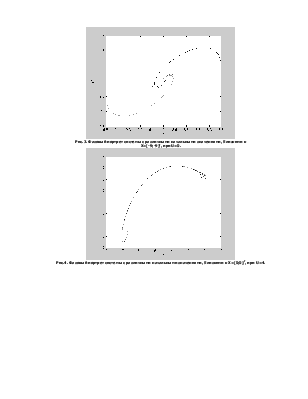
Рис.2. Фазовый портрет системы с различными начальными значениями, близкими к X=[0;0]^T, при U=0.

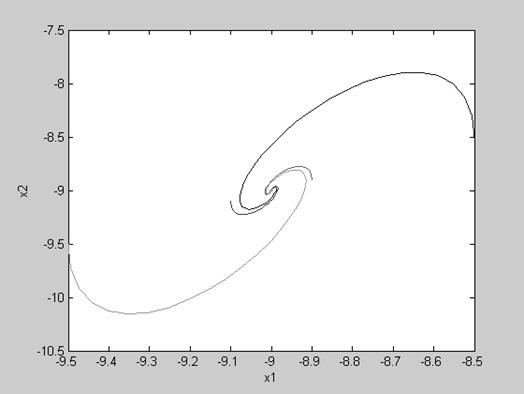
Рис.3. Фазовый портрет системы с различными начальными значениями, близкими к

X=[-9;-9]^T, при U=0.

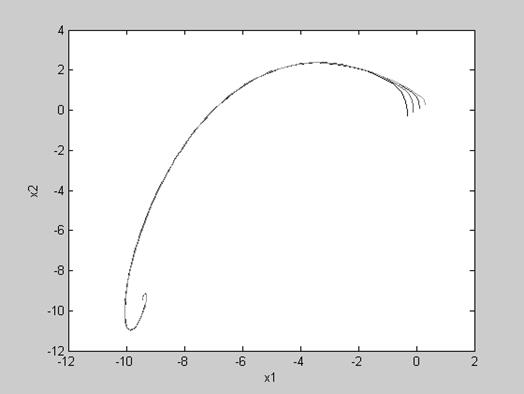
Рис.4. Фазовый портрет системы с различными начальными значениями, близкими к X=[0;0]^T, при U=4.

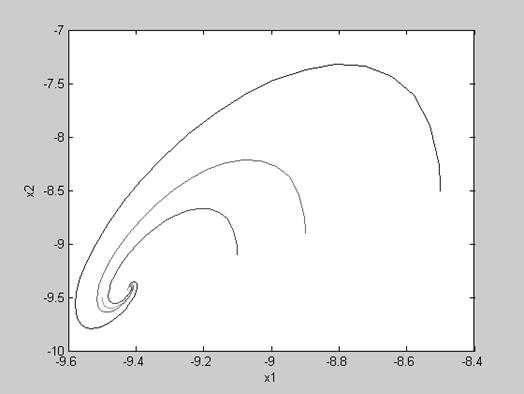
Рис.5. Фазовый портрет системы с различными начальными значениями, близкими к

X=[-9;-9]^T, при U=4.

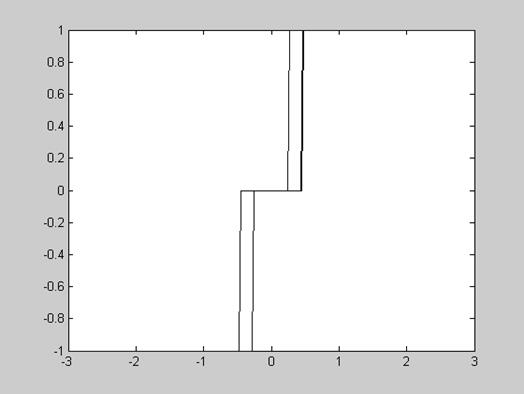
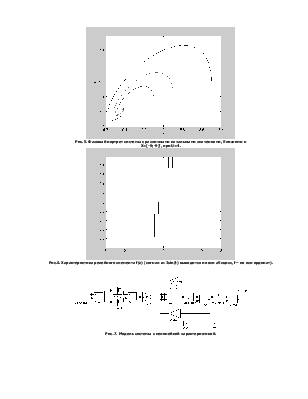
Рис.6. Характеристика релейного элемента f(z) (сигнал z=3sin(t) выводится по оси абсцисс, f – по оси ординат).

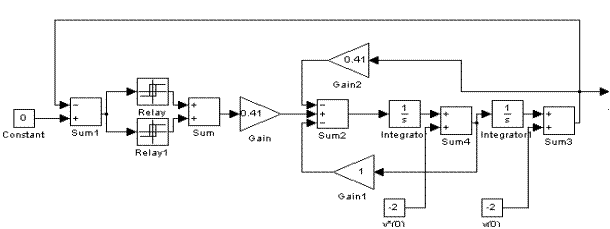
Рис.7. Модель системы с нелинейной характеристикой.

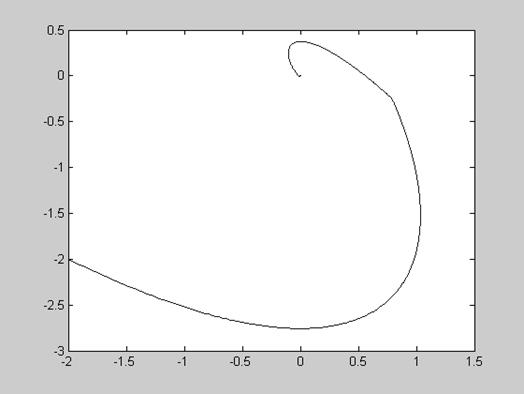
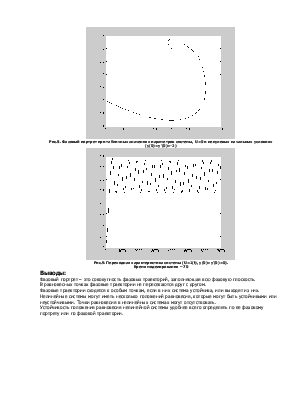
Рис.8. Фазовый портрет при табличных значениях параметров системы, U=0 и ненулевых начальных условиях (y(0)=y’(0)=-2)

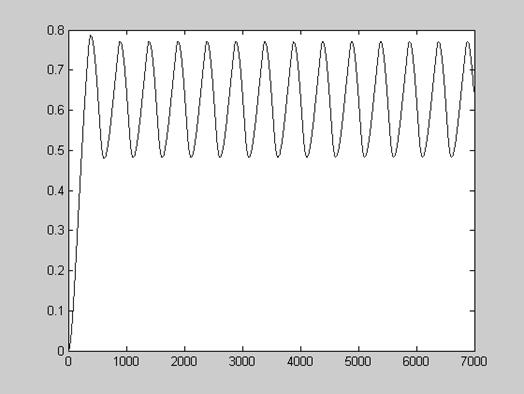
Рис.9. Переходная характеристика системы (U=1(t), y(0)=y’(0)=0).

Время моделирования – 70

Выводы:

Фазовый портрет – это совокупность фазовых траекторий, заполняющая всю фазовую плоскость.

В равновесных точках фазовые траектории не пересекаются друг с другом.

Фазовые траектории сходятся к особым точкам, если в них система устойчива, или выходят из них.

Нелинейные системы могут иметь несколько положений равновесия, которые могут быть устойчивыми или неустойчивыми. Точки равновесия в нелинейных системах могут отсутствовать.

Устойчивость положения равновесия нелинейной системы удобнее всего определять по ее фазовому портрету или по фазовой траектории.