Основы расчета простейших цепей с магнитными сердечниками

ОСНОВЫ РАСЧЕТА ПРОСТЕЙШИХ ЦЕПЕЙ

С МАГНИТНЫМИ СЕРДЕЧНИКАМИ

В большинстве магнитных устройств автоматики электромагнитные цепи, в которых использованы различные магнитные сердечники, можно подразделить на два простейших типа: дроссельные и трансформаторные.

Дроссельной цепью называют цепь, в которой обмотка на сердеч­нике включена последовательно с нагрузкой и источником питания. В этой цепи передача энергии от источника питания в нагрузку происходит при перемагничивании сердечника по частному циклу петли гистерезиса (как правило, от остаточной индукции B_r до индукции технического насыщения на колене кривой намагничивания B_m ). Если применяют сер­дечник с прямоугольной петлей намагничивания - ППГ, то на дросселе должна быть вторая обмотка, с помощью которой сердечник устанавливают в состояние с определенной остаточной индукцией.

Трансформаторная цепь имеет как минимум две обмотки на сердечнике. Передача энергии в нагрузку, подключенную к выходной обмотке, осуществляется здесь путем трансформации ее от источни­ка питания, по цепи: входная обмотка-сердечник-выходная обмотка. Сердечник в этом случае может перемагничиваться как по частному циклу, так и по полному циклу петли гистерезиса .

По характеру влияния магнитного сердечника на параметры цепи можно выделить два вида цепей. У одних цепей обмотка на сер­дечнике может быть представлена как активное нелинейное сопротивление (в этом случае сердечник обычно имеет прямоугольную петлю гистерезиса). У других цепей в обмотке происходит накоп­ление энергии электромагнитного поля и ее можно представить ли­нейной или нелинейной индуктивностью (при этом, как правило, сердечники с НПГ). В последнем виде цепей возникают различные сдвиги фаз между токами и напряжениями, что значительно усложняет анализ и расчет.

Зажимы двух обмоток принято называть одноименными, если одинаково направленные по отношению к ним токи создают в неразветвленном магнитопроводе сердечника одинаково направлен­ные магнитные потоки. Любая обмотка имеет два зажима: один ус­ловно считают ее «началом», а другой «концом» (у «начала» зажима ставится точка).

Для нахождения направления наводимых эдс и токов во всех обмотках при воздействии сигнала на одну из них существуют два правила: правило токов и правило напряжений.

Правило токов. Если возрастающий ток входит в зажим «нача­ло», то создаваемая мдс вызывает во всех других обмотках, замкнутых на нагрузку, токи, выходящие из «начала».

Правило напряжений. Если изменяющееся напряжение приложено к обмотке так, что положительный полюс эдс присоединен к зажиму «начало», то создаваемая Мдс  вызывает во всех других обмотках , положительный полюс которых также находится на зажимах «начало».

ДРОССЕЛЬНАЯ ЦЕПЬ ПЕРЕМЕННОГО ТОКА НА СЕРДЕЧНИКАХ С НПГ

Расчет цепи переменного тока с сердечником любого типа можно вести с помощью нелинейных или линеаризованных методов.

Нелинейные методы расчета позволяют определить форму кривых напряжений и токов в отдельных участках цепи, а также величину и фазу отдельных гармоник. Однако решать нелинейные дифференциальные уравнения трудно.

В линеаризованных методах расчета при выводе основных соотношений магнитную проницаемость m, например, полагают посто­янной величиной, а цепи- линейными. Лишь при окончательном расчете входящая в полученные формулы m считается функцией Н, заданной в основном в виде экспериментальных интегральных характеристик.

Ниже рассматривается наиболее распространенный линеаризованный метод расчета на примере простейшей дроссельной цепи с магнитным кольцевым сердеч­ником с НПГ, рис.1.

Рис.1.Простейшая электромагнитная цепь переменного тока с дросселем из

       магнитного сердечника (а) и ее эквива­лентные схемы (б)  и  (в)

Пусть необходимо в этой цепи определить действующее  значение тока I в зависимости от действующего значения питающего синусоидального напряжения и при активной нагрузке дросселя Z_н=R_н.

Действующие значение интегральной характеристи­ки по закону полного тока:

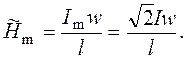                                                                                                                                            (1)

При величина,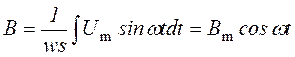

где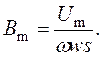

Тогда:

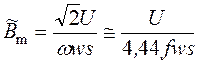.                                                              (2)

 Сопротивление дросселя в комплексной форме (без учета актив­ного сопротивления обмоток, включенного в R_н) при использовании (1) и (2):

                                                        ,   

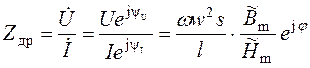где  разность фаз между напряжением и током в рассматриваемой цепи. 

Сопротивление дросселя при  , :

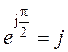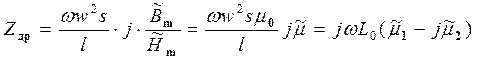,             (3)

или   

,

где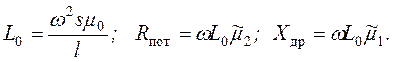

Таким образом, при определении действующего значения тока схему (рис.1, а) можно заменить эквивалентной схемой, представленной на рис.1, б , в которой

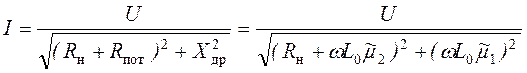.      (4)

Пусть известно число витков обмотки, геометрические размеры сердечника и его интегральные магнитные характеристики, в частности, зависимости упругой  и вязкой  составляющих комплекс­ной проницаемости от величины напряженности поля .Задава­ясь для разных моментов времени различными значениями дейст­вующего тока I, по выражению (1) можно определить , затем из экспериментальных характеристик  и - соответ­ствующие значения  и  и, пользуясь уравнением (4), постро­ить зависимость U(t) для рассматриваемой схемы.

Часто в дроссельных цепях , тогда уравнение (4) можно упростить:

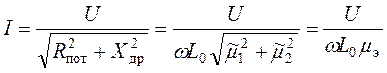,                             (5)

где  - эквивалентная проницаемость, представляющая собой модуль комплексной проницаемости.

Если имеет место соотношение R_н>>R_пот или , что так же часто встречается на практике, то уравнение (4) мож­но записать в следующем виде:

,                                         (6)

где U_Rи U_L - соответственно активное и индуктивное падения на­пряжения в рассматриваемой цепи.

Практически применяют еще параллельную схему замещения дроссельной цепи рис.1, в, которая более правильно отражает сущность влияния потерь с помощью сопротивления R_//, включенно­го параллельно индуктивности L_//. С ростом потерь в сердечнике величина R_//,  уменьшается, в то время как L_// (в отличие от X_др в схеме рис.1,б) может не изменяться при отсутствии поверхност­ного эффекта. Дроссель в такой эквивалентной схеме характеризуется комплексной проводимостью