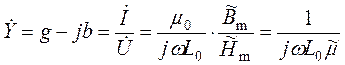 . (7)
. (7)
Вводя комплексное удельное магнитное сопротивление ![]() , имеем:
, имеем:
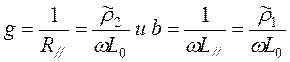 , (8)
, (8)
где 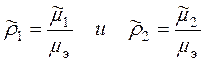 .
.
ИМПУЛЬСНЫЕ ТРАНСФОРМАТОРЫ НА СЕРДЕЧНИКАХ С НПГ
Наиболее распространенным, режимом намагничивания сердечников с НПГ в импульсных трансформаторах является режим воздействия однополярных импульсов тока или напряжения. Однополярное, например, положительное намагничивание характеризуется ветвью статической петли гистерезиса, распространяющейся от состояния Br в сторону больших положительных индукций. Часто подобную ветвь представляют в координатах DB; H (рис.2)., где DB=B-Br.
|
Рис.2. Зависимости для трансформатора на сердечнике с НПГ |
Из
рис.2. ясно: чем больше начальная магнитная проницаемость mнач
сердечников, тем очевиднее, что на кривых ![]() необходимо выделить два участка с разными
проницаемостями на частном цикле
необходимо выделить два участка с разными
проницаемостями на частном цикле ![]() . В импульсных трансформаторах сердечники, как
правило, работают в линейном режиме. Поэтому рабочую точку сердечника нужно
выбирать на одном из линейных участков, где mD=const. Границей раздела этих участков является
величина DB0.
. В импульсных трансформаторах сердечники, как
правило, работают в линейном режиме. Поэтому рабочую точку сердечника нужно
выбирать на одном из линейных участков, где mD=const. Границей раздела этих участков является
величина DB0.
|
Рис.3. Электромагнитная цепь импульсного трансформатора на сердечнике с НПГ |
Ниже
рассматриваются основные уравнения, определяющие работу импульсного
трансформатора, питающегося от источника напряжения, при активном характере
нагрузки на выходе (рис.3.). За время действия импульса напряжения ![]() с
постоянной амплитудой Um и длительностью
с
постоянной амплитудой Um и длительностью ![]() индукция в сердечнике изменится на величину
индукция в сердечнике изменится на величину ![]() ,
определяемую как
,
определяемую как
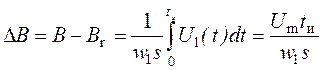 .
(9)
.
(9)
Согласно правилу токов во вторичной цепи будет
протекать ток ![]() , создающий Мдс.,
противодействующую намагничивающей. Ток, определяющий намагничивающее поле в
сердечнике (так называемый ток намагничивания
, создающий Мдс.,
противодействующую намагничивающей. Ток, определяющий намагничивающее поле в
сердечнике (так называемый ток намагничивания ![]() ), находят из уравнения
), находят из уравнения ![]() . После
преобразований и ввода коэффициента трансформации
. После
преобразований и ввода коэффициента трансформации ![]() можно
записать
можно
записать
![]() . (10)
. (10)
Намагничивающий ток можно выразить через величину ![]() , используя закон полного
тока и уравнение (9):
, используя закон полного
тока и уравнение (9):
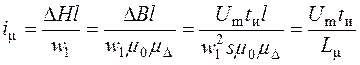 , (11)
, (11)
где 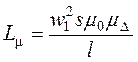 - индуктивность намагничивания.
- индуктивность намагничивания.
Ток во вторичной цепи ![]() определяется напряжением
определяется напряжением ![]() и сопротивлением
нагрузки:
и сопротивлением
нагрузки: ![]() .
На основе закона электромагнитной индукции напряжение
.
На основе закона электромагнитной индукции напряжение
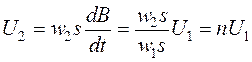 . (12)
. (12)
Таким образом, анализируя уравнения (10), (11) и (12),
импульсный трансформатор можно представить в виде простейшей эквивалентной
схемы, как показано на рис.4. Здесь величина ![]() представляет
собой приведенный к первичной цепи ток, протекающий в нагрузке, a
представляет
собой приведенный к первичной цепи ток, протекающий в нагрузке, a ![]() , также приведенное к первичной цепи, - сопротивление
нагрузки. Величину его можно определить, рассматривая последовательно
, также приведенное к первичной цепи, - сопротивление
нагрузки. Величину его можно определить, рассматривая последовательно ![]() , выражение (12) и эквивалентную схему:
, выражение (12) и эквивалентную схему:
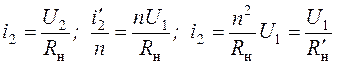 ,
,
где ![]() .
.
Временная диаграмма работы импульсного трансформатора представлена на рис.4.
В
действительности напряжение на вторичной обмотке трансформатора в течение
времени ![]() не
остается постоянным и равным
не
остается постоянным и равным ![]() . Оно будет
изменяться по закону
. Оно будет
изменяться по закону
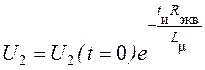 .
.
Здесь 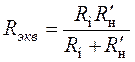 ,
,
где ![]() - внутреннее сопротивление источника импульсов напряжения.
- внутреннее сопротивление источника импульсов напряжения.
|
|
|
|
а б
Рис.4. Простейшая эквивалентная схема (а) и временная диаграмма работы импульсного
трансформатора (б).
В
результате этого на вершине импульса будет наблюдаться спад напряжения ![]() (см.
пунктирную линию на верхней диаграмме, рис. 4, б), %
(см.
пунктирную линию на верхней диаграмме, рис. 4, б), %
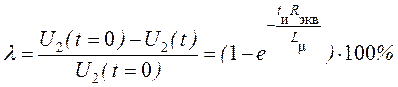 .
(13)
.
(13)
Так как основным определяющим параметром импульсного
трансформатора является (о чем свидетельствует эквивалентная схема рис.4, а)
индуктивность намагничивания ![]() , то в такой
цепи должно наблюдаться отставание изменений тока от изменения напряжения и
связанное с ним накопление энергии в индуктивности (см. рис.4, б). Это
же свойство обусловливает появление всплеска напряжения обратного знака после
окончания действия входного импульса напряжения
, то в такой
цепи должно наблюдаться отставание изменений тока от изменения напряжения и
связанное с ним накопление энергии в индуктивности (см. рис.4, б). Это
же свойство обусловливает появление всплеска напряжения обратного знака после
окончания действия входного импульса напряжения ![]() .
Длительность всплеска определяется постоянной времени эквивалентной цепи:
.
Длительность всплеска определяется постоянной времени эквивалентной цепи:
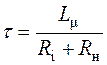 ,
,
а амплитуду всплеска :
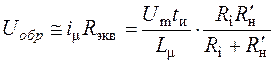 .
(14)
.
(14)
После
окончания переходных процессов на срезе входного импульса напряжения, т. е.
через время ![]() , импульсный трансформатор готов к передаче следующего
импульса той же полярности.
, импульсный трансформатор готов к передаче следующего
импульса той же полярности.
Более полная эквивалентная схема импульсного трансформатора должна учитывать все паразитные параметры, присутствующие в реальной электромагнитной цепи (паразитные емкости первичной, вторичной цепи, индуктивность рассеяния и т. п.), и эквивалентные параметры потерь (омические и реактивные потери на гистерезис, вихревые токи и магнитную вязкость). Такая эквивалентная схема описывается дифференциальным уравнением 4-го порядка. Сложность решения его можно преодолеть путем анализа процессов в импульсном трансформаторе на различных стадиях работы: передача переднего фронта и среза трансформируемого импульса, формирование вершины импульса. В этом случае сложную эквивалентную схему можно свести на каждой стадии к более простой, подобно рассмотренной.
Пример.
Рассчитать число витков первичной обмотки и индуктивность, вносимую в
первичную цепь повышающим импульсным трансформатором, выполненным на
сердечнике с НПГ размерами К10x6x2 мм из материала 1500НМ1. Сердечник
работает на первом участке зависимости ![]() и предназначен для передачи с повышением по напряжению
в два раза прямоугольных импульсов длительностью
и предназначен для передачи с повышением по напряжению
в два раза прямоугольных импульсов длительностью ![]() =1 мкс и
амплитудой
=1 мкс и
амплитудой ![]() =5
В. Допустимый спад напряжения
=5
В. Допустимый спад напряжения ![]() =2%, внутреннее сопротивление источника импульсов
=2%, внутреннее сопротивление источника импульсов ![]() =500 Ом,
сопротивление нагрузки
=500 Ом,
сопротивление нагрузки ![]() =100 Ом.
=100 Ом.
Геометрические
параметры сердечника: s=4 мм2, ![]() мм. Согласно рис.2. на первом участке зависимости
мм. Согласно рис.2. на первом участке зависимости ![]()
![]() = 1370.
= 1370.
При
малой величине спада ![]() (когда
(когда 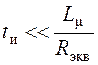 из выражения (13) можно, разлагая в ряд, приближенно получить, что
из выражения (13) можно, разлагая в ряд, приближенно получить, что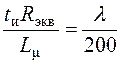 .Отношение
.Отношение![]() можно
выразить с учетом входящих величин:
можно
выразить с учетом входящих величин:
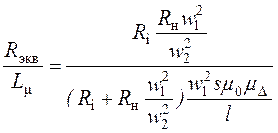 =
=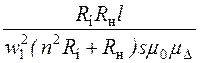 .
.
Подставляя
его в предыдущее соотношение и решая относительно ![]() ,
имеем
,
имеем
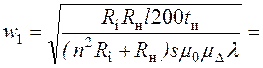
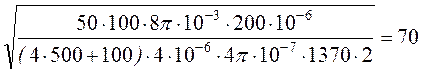 .
.
Индуктивность первичной обмотки
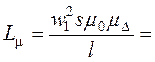
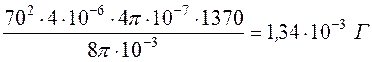 .
.
Согласно (14) можно оценить величину выброса при ![]() :
:
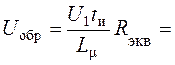
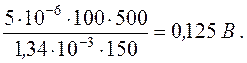
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.