О модели перевернутого маятника

СБОРНИК НАУЧНЫХ ТРУДОВ НГТУ. – 2012. – № 1(__). – 3–10

автоматическое управление
и идентификация

УДК 681.513

О МОДЕЛИ ПЕРЕВЕРНУТОГО МАЯТНИКА*

А.А. Воевода, Е.В.ШОБА

Приведены нелинейные и линеаризованные модели перевернутого маятника на тележке, соответствующие различным случаям, а именно, при нулевой массе тележки с учетом и без учета момента инерции маятника. Проанализированы две структурные схемы модели, одна из которых включает так называемое “алгебраическое кольцо”.

Ключевые слова: перевернутый маятник, тележка, модель объекта.

ВВЕДЕНИЕ

В качестве одного из излюбленных примеров анализа и синтеза систем управления берут перевернутый маятник на тележке, например [1, 2]. В одних работах используют дифференциальные уравнения, содержащие каждое вторые производные положения и угла наклона маятника, в других преобразовывают таким образом, что в каждом уравнении остается по одной “старшей производной” и, как следствие, эти уравнения удобны в расчетах и моделировании. Особый интерес представляют эти модели в случае, когда моментом инерции маятника можно пренебречь, а также случай, когда масса тележки существенно меньше массы маятника и ее можно положить равной нулю. Эти вопросы рассмотрены в данной статье.

1.МОДЕЛЬ “ПЕРЕВЕРНУТЫЙ МАЯТНИК НА ТЕЛЕЖКЕ”

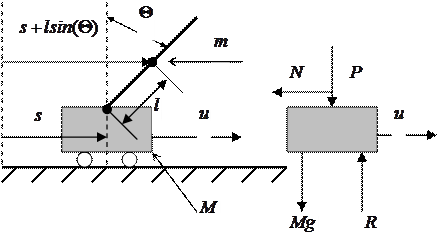
Рассмотрим перевернутый маятник на тележке (Рис.1): - масса тележки, - масса маятника, - координата центра тяжести тележки (по горизонтальной оси - расстояние от центра тяжести, - координата центра тяжести маятника (по горизонтальной оси), - отклонение маятника от вертикали, - сила, приложенная к тележке, , - силы, вызванные воздействием маятника на тележку (Рис.1б) и воздействием тележки на маятник (Рис.1в), - реакция опоры на тележку, - вес маятника, - момент инерции маятника относительно центра тяжести.

 

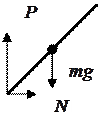Рис.1а. Маятник на тележке                    Рис.1б. Тележка-       Рис.1в. Маятник-

                                                                              баланс сил                 баланс сил

Систему опишем уравнениями – используем баланс сил.

Тележка - баланс сил по горизонтали

                                                    (1)

и баланс сил по вертикали

.                                               (2)

Маятник- баланс сил по горизонтали

.

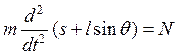Продифференцируем

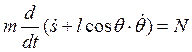
и еще раз продифференцируем

.                            (3)

Маятник – баланс сил по вертикали

.

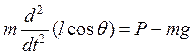Продифференцируем

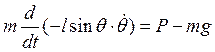
и еще раз продифференцируем

.                       (4)

Кручение маятника

.                                   (5)

Система «тележка - маятник» описывается уравнениями (1 – 5). Уравнение (2) можно исключить из рассмотрения, так как реакция опоры присутствует только в уравнении (2), из которого его можно вычислить. Другими словами, система описывается уравнениями (1), (3)-(5).

Исключим  из (3), для чего выразим  из (1) и подставим в (3):

.                    (6)

Исключим  и  из (5) – возьмем их из (3) и (4) и подставим в (5):

.

Сократив первый и предпоследний члены, а также сгруппировав второй и последний, получим

.                              (7)

Теперь система описывается уравнениями (6) и (7) – в них входят три переменные -  управляющая переменная , положение тележки  и наклон маятника . Эти уравнения не очень удобны для исследования, например, для моделирования, так как старшие производные второго порядка входят в оба уравнения.

Избавимся от этого недостатка – преобразуем уравнения (6) и (7). Вначале поделим уравнение (7) на  и введем обозначение :

.

Значение  подставим в (6), которое перепишем виде ()

,

откуда

.

Перегруппируем

и поделим на :

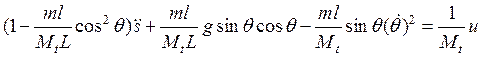.   (8)

Уравнение (6) преобразовано в (8).

Преобразуем уравнение (7), для чего возьмем  из (6)

и подставим в (7):

.

Полученное выражение поделим на :

.

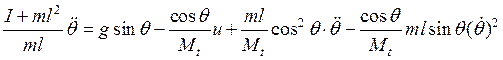После деления на  и переноса всех членов, кроме второго, налево, получим

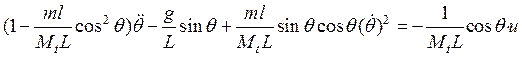.  (9)

Система “перевернутый маятник на тележке” описана уравнениями (8) и (9), где , . Эти уравнения удобны для моделирования, так как в каждое из них входит по одной старшей производной. При выводе предполагалось, что  и .

Примечание. Схема данного вывода, содержащая многочисленные опечатки, приведена в [1].

Частный случай , .

Уравнение (1) преобразуется в уравнение

     ,                                                  (1а)

Уравнения (3) – (5) не изменяются. Берем  из (1а) и подставляем в (3)

                            (6а)

Аналогично общему случаю исключим  и  из (5) – возьмем их из (3) и (4) и подставим в (5), получим

,                              (7а)

полностью совпадающее с (7). Итак, при  система описывается (6а) и (7а). Преобразуем (6а) и (7а) аналогично преобразованиям (6) и (7): (7а) делим на  -    . Значение  подставим в (6а), которое перепишем виде :

.

Перегруппируем

и поделим на :

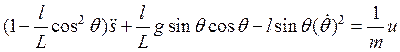.   (8а)

Уравнение (6а) преобразовано в (8а).

Преобразуем уравнение (7а), для чего возьмем  из (6а)

И подставим в (7а):

.

Полученное выражение поделим на :

.

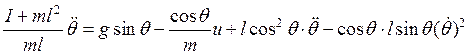После деления на  и переноса всех членов, кроме второго, налево, получим

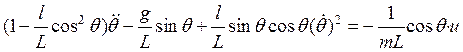.     (9а)

Система “перевернутый маятник на тележке” описана уравнениями (8а) и (9а), где . Формально (8а), (9а) можно было получить из (8), (9) заменой  на .

Частный случай , . Измениться уравнение (5):

.                                   (5б)

Выразим  из (1) и подставим в (3) (получили уравнение (6), но для удобства обозначим его (6б)):

.                    (6б)