О модели перевернутого маятника, страница 2

Возьмем  и  из (3) и (4) и подставим в (5б). После преобразований получим частный случай (7):

.                              (7б)

Теперь система описывается уравнениями (6б) и (7б). Преобразуем уравнения (6б) и (7б). Вначале поделим уравнение (7б) на :

.

Формально . Значение  подставим в (6б) и учтем, что :

.

Перегруппируем

и поделим на :

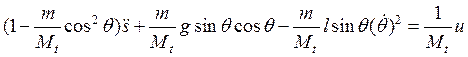.   (8б)

Уравнение (8б) можно формально получить из (8), если учесть, что .

Нужно вывести (9) но с условием, что .

Преобразуем уравнение (7б), для чего возьмем  из (6б)

и подставим в (7б):

.

Полученное выражение поделим на :

.

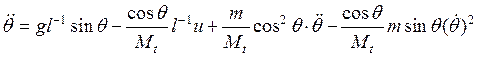После переноса всех членов, кроме второго, налево, получим

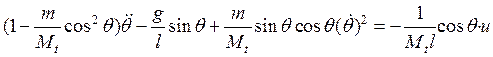.  (9б).

Уравнение (9б) можно формально получить из (9) заменой .

Система “перевернутый маятник на тележке” описана уравнениями (8б) и (9б), где .

Частный случай , . Уравнение (1) преобразуется в уравнение

     .                                                  (1с)

Измениться уравнение (5):

.                                   (5с)

Уравнения (3), (4) не изменяются. Берем  из (1с) и подставляем в (3)

                            (6с)

Аналогично общему случаю исключим  и  из (5с) – возьмем их из (3) и (4) и подставим в (5с), получим

,                              (7с)

Поделим уравнение (7с) на :

.

Значение  подставим в (6с):

.

Перегруппируем

и поделим на :

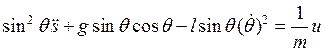.                 (8с)

Аналогично выводу в общем случае из (6с)  подставляем в (7с) и после простых преобразований получим

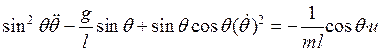.     (9с).

Получили описание системы в виде (8с) и (9с), которое можно было получить из (8) и (9) формальным приравниванием нулю , .

2.ЛИНЕАРИЗОВАННАЯ МОДЕЛЬ

Общий случай , . Линеаризацию осуществляем в окрестности точки  и  - в уравнениях (8) и (9) полагаем , , :

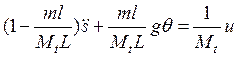.                                (10)

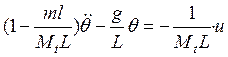.                                (11)

Обозначим через 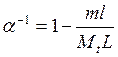. Тогда (10), (11) преобразуются в

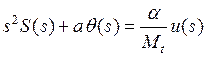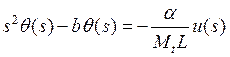, .     (12а, 12б)

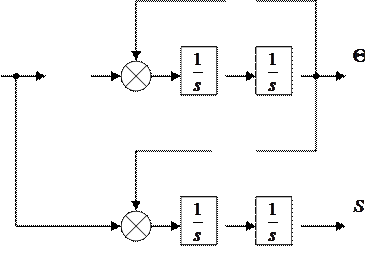
Здесь написали аргумент , чтобы подчеркнуть, что изображение положения тележки  записывается так . Ниже приведена структурная схема объекта, где , .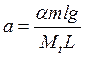

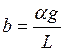Рис.2. Структурная схема объекта, соответствующая (10), (11).

Несложно выписать передаточную функцию по каналу :

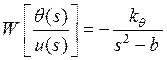,                                       (13)

где 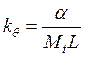. Чуть сложнее выписать передаточную функцию 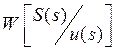: для этого (12а) умножим на

,

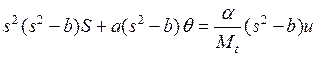а из (12б) выпишем 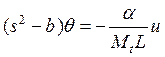 и подставим в предыдущее выражение

.

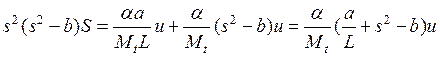Наконец

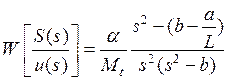.                             (14)

Примечание. Если линеаризуем уравнения (6) и (7), получим

,                                       

.

Во втором уравнении все члены перенесем налево:

.                                   

Уравнения   и  совпадают с уравнениями, используемыми в [2], если положить  равным нулю.  Соответствующая структурная схема приведена на рис.2.

            

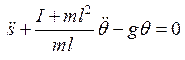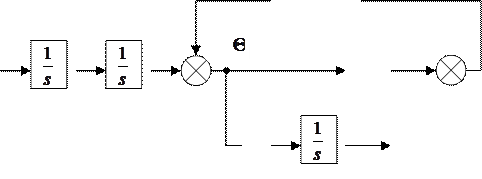
Рис.2. Структурная схема, соответствующая уравнениям  и

Частный случай , , (, ):

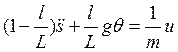.                                 (10а)

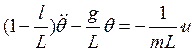.                              (11а)

На рис.2 параметры принимают следующие значения:

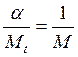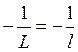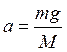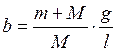, , ,  так как .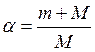

Частный случай , :

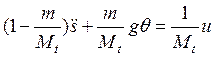.                             (10б)

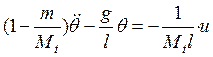.                            (11б).

Частный случай ,  не рассматриваем.

ЗАКЛЮЧЕНИЕ

В литературе часто встречаются модели перевернутого маятника на тележке, существенно отличающиеся друг от друга. При этом выводы даются неполно и с опечатками. В данной работе подробно рассмотрен вывод модели перевернутого маятника в двух вариантах – один вариант удобен для моделирования и анализа, а другой легче получить, но труднее использовать, так как при его моделировании в структуре появляется алгебраическое кольцо. Кроме того, приведены модели для частных случаев – при равенстве нулю массы тележки и (или) момента инерции маятника.

[1] M.Dahleh, M.A.Dahleh, G.Verghese. Lectures on dynamic systems and control. 2003. Massachuasetts Institut of technology. 600 p.

[2] J.Doyle, B.Francis, A.Tannenbaum. Feedback control theory. Macmillan Publishing. 1990. 198 p.

Воевода Александр Александрович - профессор кафедры автоматики Новосибирского государственного технического университета. 

e-mail: ucit@ucit.ru.

Шоба  Евгений Владимирович - соискатель кафедры автоматики Новосибирского государственного технического университета.

E-mail: nsk_nstu@mail.ru.

A.A. Voevoda,  E.V. Shoba. ABOUT MODEL INVERTED PENDULUM.

The nonlinear and linearized models of the inverted pendulum are given in the cart, corresponding to various cases, namely, at zero mass of the cart with the account and without the moment of inertia of a pendulum. Two block diagrams of the model one of which includes so-called “an algebraic ring” are analysed.

Keywords: the inverted pendulum, the cart, object model.