Исследование итерационного метода спуска решения нелинейного алгебраического уравнения, страница 3

 0.1E-08   -9.000    0.7105E-15     -15.148    0.2610E-15        -15.583    9        24

 0.1E-07   -8.000    0.8021E-10     -10.096    0.2704E-10         -10.568    9        23

 0.1E-06   -7.000    0.8021E-10     -10.096    0.2704E-10      -10.568    9        23

 0.1E-05   -6.000    0.8021E-10     -10.096    0.2704E-10      -10.568    9        23

 0.1E-04   -5.000    0.8021E-10    -10.096    0.2704E-10       -10.568    9        23

 0.1E-03   -4.000    0.4447E-09      -9.352    0.3507E-09       -9.455      8        21

 0.1E-02   -3.000    0.8980E-05      -5.047    0.4270E-05       -5.370      8        20

 0.1E-01   -2.000    0.8980E-05      -5.047    0.4270E-05       -5.370      8        20

 0.1E+00   -1.000    0.8980E-05     -5.047    0.4270E-05       -5.370      8        20

 0.1E+01    0.000    0.4636E-02     -2.334    0.1703E-02       -2.769      7        17

Влияние параметра EPS на точность и количество итераций. N=6, Xi= –8,  iÎ [1, 6]

EPS	lgESP	EMO	lgEMO	ECO	lgECO	KM	KMO
0.1E-08	-9.000	0.4364E-01	-1.360	0.7870E-02	-2.104	39	76
0.1E-07	-8.000	0.6269E-01	-1.203	0.1131E-01	-1.947	37	72
0.1E-06	-7.000	0.9023E-01	-1.045	0.1628E-01	-1.788	35	68
0.1E-05	-6.000	0.1299E+00	- 0.886	0.2344E-01	-1.630	33	64
0.1E-04	-5.000	0.1884E+00	-0.725	0.3394E-01	-1.469	31	59
0.1E-03	-4.000	0.3258E+00	-0.487	0.5868E-01	-1.231	28	53
0.1E-02	-3.000	0.7297E-01	-1.137	0.6399E-01	-1.194	26	65
0.1E-01	-2.000	0.6629E+00	-0.179	0.1201E+00	-0.921	24	44
0.1E+00	-1.000	0.1167E+00	-0.933	0.1174E+00	-0.930	22	49
0.1E+01	0.000	0.1006E+01	0.002	0.1584E+00	-0.800	20	52

Сходимость оценки первого выделяемого корня

     K       alfa X1           beta X1

     0  -0.3000D+02   0.2500D+02

     1  -0.2583D+02   0.2083D+02

     2  -0.2236D+02   0.1736D+02

     3  -0.1947D+02   0.1447D+02

     4  -0.1706D+02   0.1206D+02

     5  -0.1505D+02   0.1005D+02

     6  -0.1337D+02   0.8372D+01

     7  -0.1198D+02   0.6977D+01

     8  -0.1081D+02   0.5814D+01

     9  -0.9845D+01   0.4845D+01

    10  -0.9038D+01   0.4038D+01

    11  -0.8365D+01   0.3365D+01

    12  -0.7804D+01   0.2804D+01

    13  -0.7337D+01   0.2337D+01

    14  -0.6947D+01   0.1947D+01

    15  -0.6623D+01   0.1623D+01

    16  -0.6352D+01   0.1352D+01

    17  -0.6127D+01   0.1127D+01

    18  -0.5939D+01   0.9390D+00

    19  -0.5783D+01   0.7825D+00

    20  -0.5652D+01   0.6521D+00

    21  -0.5543D+01   0.5434D+00

    22  -0.5453D+01   0.4528D+00

    23  -0.5377D+01   0.3774D+00

    24  -0.5314D+01   0.3145D+00

    25  -0.5262D+01   0.2621D+00

    26  -0.5218D+01   0.2184D+00

    27  -0.5182D+01   0.1820D+00

    28  -0.5152D+01   0.1517D+00

    29  -0.5126D+01   0.1264D+00

    30  -0.5105D+01   0.1053D+00

    31  -0.5088D+01   0.8776D-01

    32  -0.5073D+01   0.7314D-01

    33  -0.5061D+01   0.6095D-01

    34  -0.5051D+01   0.5079D-01

    35  -0.5042D+01   0.4233D-01

lg Emo=f(lgEPS)-синий;KMO = f(lg EPS)                          Графики сходимости первых выделяемых   

                                                                      корней   типа 5

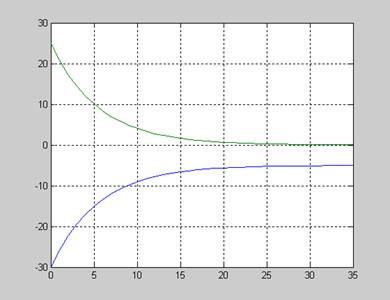
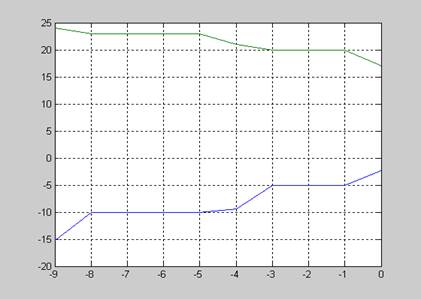
                                              Рис.1                                                                                            рис.2

Выводы

Исследовали  итерационный метод спуска решения нелинейного алгебраического уравнения. Проанализировали  влияния вида корней и параметра останова на точность (количество итераций) определения корней. Получили:

  1) Чем меньше   параметр e, тем меньше EMO – максимальная относительная погрешность между действительными и мнимыми частями истинных комплексных корней и их оценками и ESO – среднеквадратичная относительная погрешность между истинными корнями уравнения и их оценками.

  2) Чем меньше   параметр e, тем больше  KMO  – общее количество итераций, полученное при выделении всех корней уравнения и  KM – максимальное количество итераций, полученное при выделении одного из корней уравнения.

Из Табл .2  видно, что корни вида 2 имеет  самую маленькую относительную погрешность, а корни вида 5 – самую большую.