Изучение свойств непрерывной адаптивной системы, синтезированной на основе второго метода Ляпунова, страница 2

Для улучшения процессов в системе изменить значения , , сравнить результат с  п. 3.5.

а) =1, =1, γ₁=500, γ₂=0,1

                y

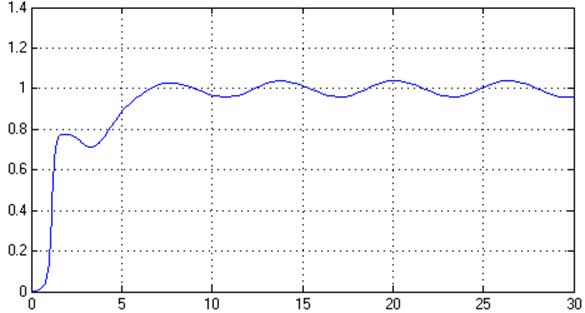t

Рис. 23. Переходный процесс в системе, y(t) (% = 4%, t_пп = 5,8 с)

.

          

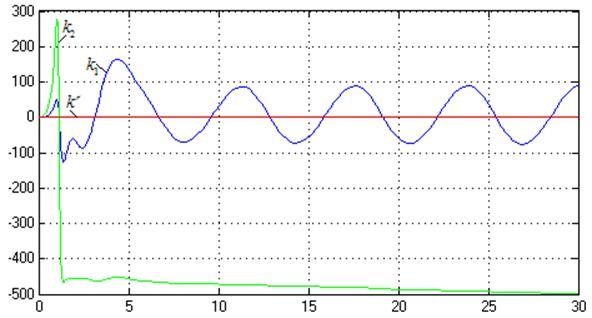t

Рис.24. Процессы на выходе адаптера ,.

               U

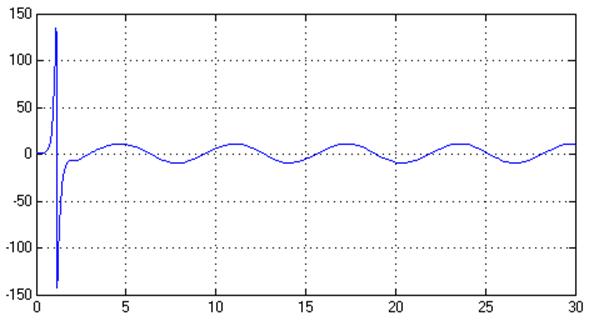t

Рис.25. Управляющее воздействие, U(t)

б) =1, =10, γ₁=150, γ₂=1

                       y

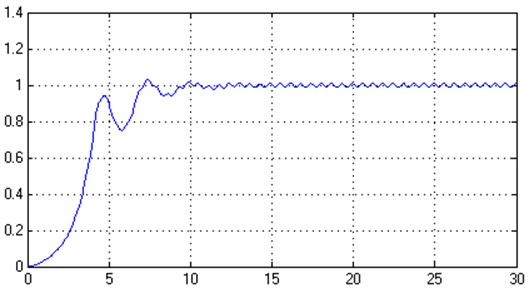t

Рис. 26. Переходный процесс в системе, y(t) (% = 3%, t_пп = 9 с)

.

            

t

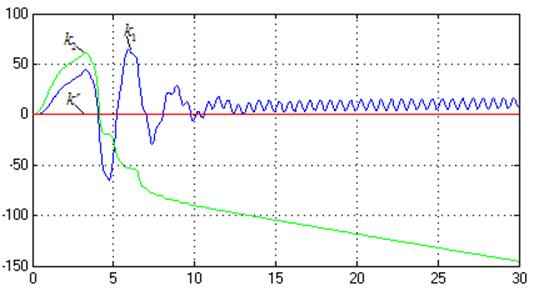
                              Рис.27. Процессы на выходе адаптера (,).

                       U

t

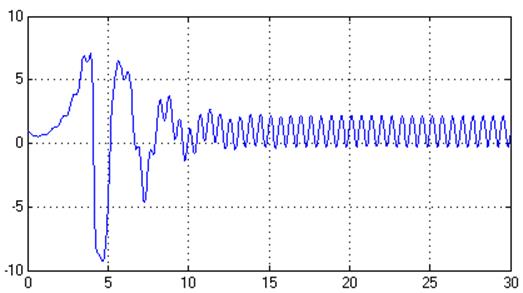
Рис.28. Управляющее воздействие, U(t)

в) =10, =1, γ₁=700, γ₂= 0.001

                  y

t

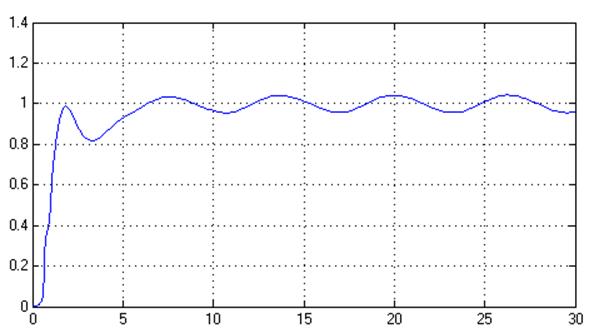
Рис.29. Переходный процесс в системе, y(t) (% = 4%, t_пп = 5,4 с)

           

t

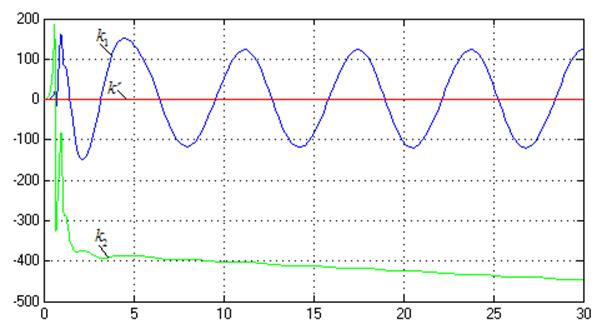
Рис.30. Процессы на выходе адаптера (,).

                     U                

t

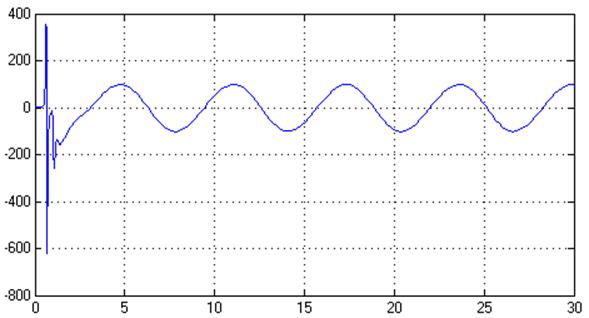
Рис.31. Управляющее воздействие, U(t)

3.11 Собрать схему системы с наблюдателем. Выполнить исследования системы, повторив пп. 3.5, 3.6, 3,9.

пп 3.5.

                       y

t

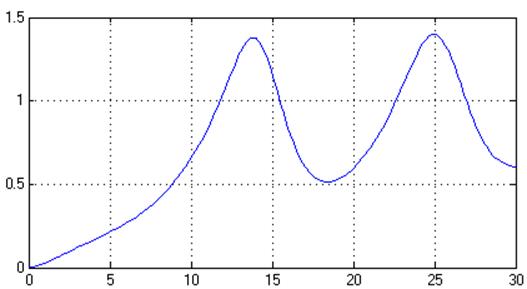
Рис. 32. Переходный процесс в адаптивной системе с наблюдателем, показатели качества являются не удовлетворительными.

                          U

t

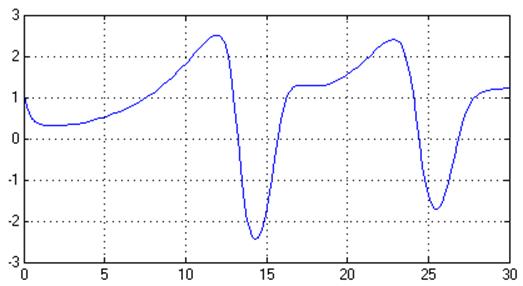
Рис. 33. Управляющее воздействие, U(t)

                 

t

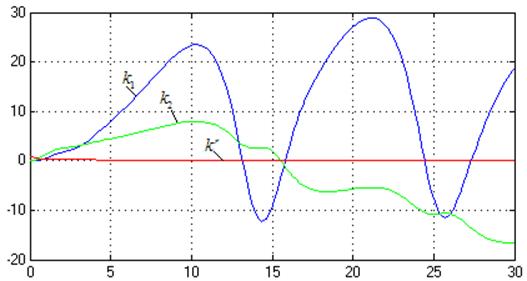
Рис. 34. Переходные процессы

пп 3.6.

 γ = 200, 200, 1

                          y

t

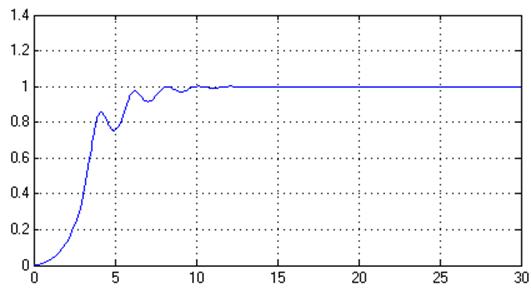
Рис. 35. Переходный процесс в адаптивной системе с наблюдателем (% = 1%, t_пп = 7,5 с)

                          U

t

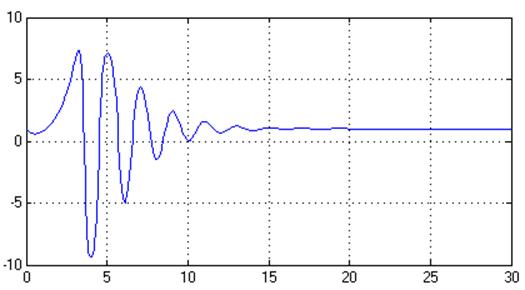
Рис. 36. Управляющее воздействие, U(t)

                 

t

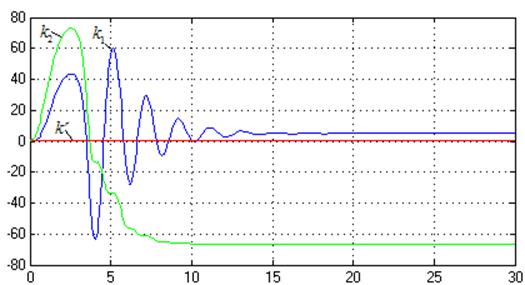
Рис. 37. Переходные процессы (t_1ппа=22 с, t_2ппа=14 с, t^r_ппа=4,7 с)

пп 3.9

а) =1, =1, γ₁=500, γ₂=0,1

                       y

t

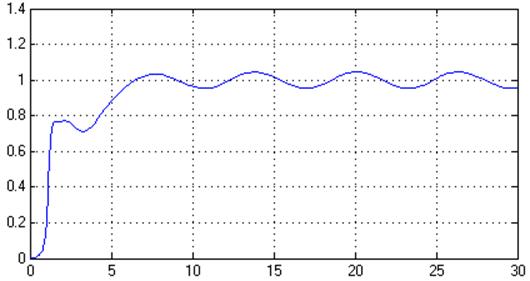
Рис. 38. Переходный процесс в системе, y(t) (% = 4,5%, t_пп = 5,7 с)

               

t

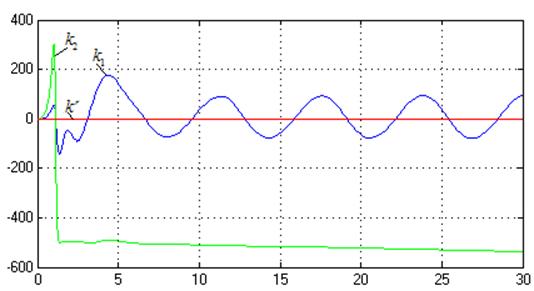
                              Рис.39. Процессы на выходе адаптера (,).

                       U

t

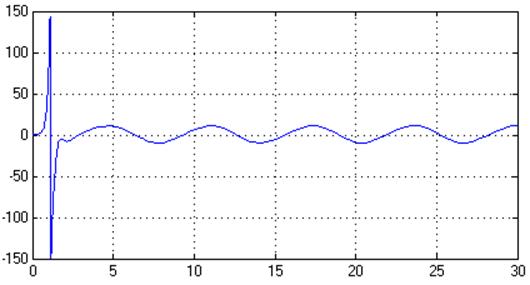
Рис.40. Управляющее воздействие, U(t)

б) =1, =10, γ₁=150, γ₂=1

                       y

t

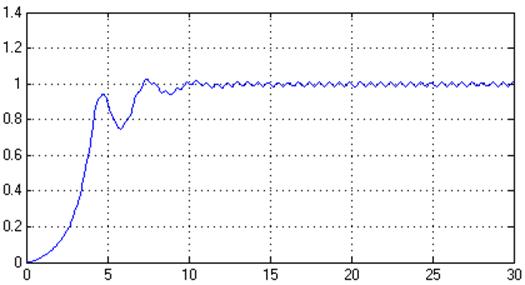
Рис. 41. Переходный процесс в системе, y(t) (% = 3%, t_пп = 9 с)

.

               

t

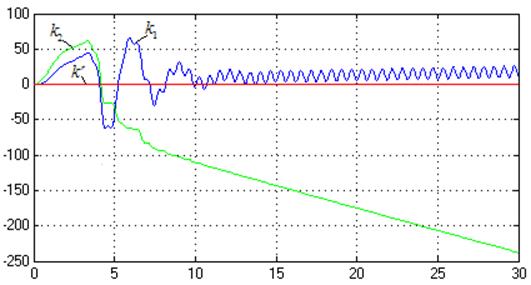
                              Рис.42. Процессы на выходе адаптера (,).

                       U

t

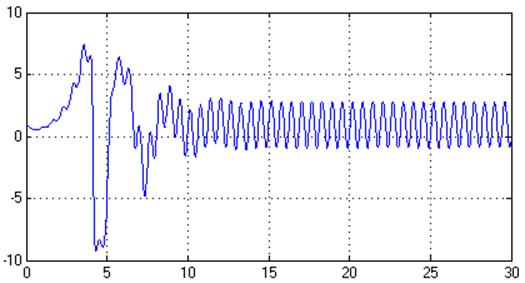
Рис.43. Управляющее воздействие, U(t)

в) =10, =1, γ₁=700, γ₂= 0.001

                       y

t

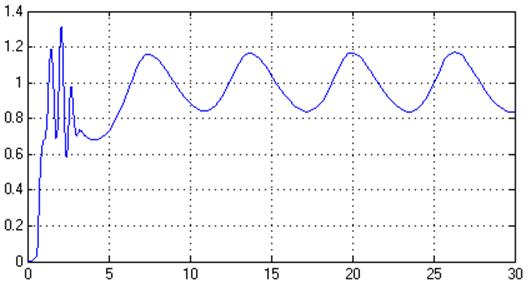
Рис.44. Переходный процесс в системе, y(t) не удовлетворяет желаемому

                

t

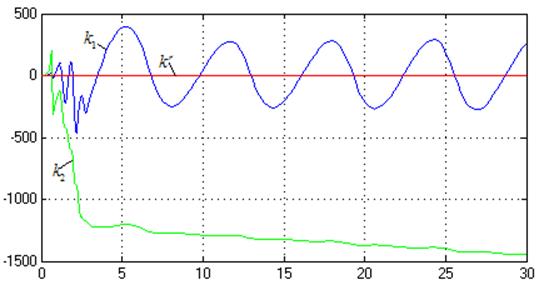
Рис.45. Процессы на выходе адаптера (,).

t

                           U                 

t

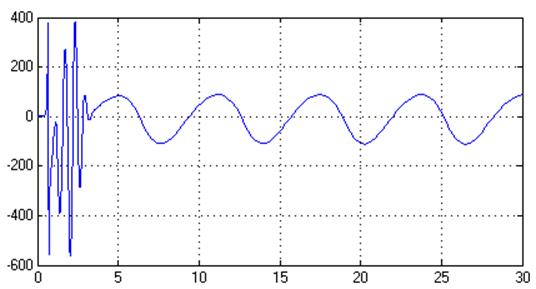
Рис.46. Управляющее воздействие, U(t)

Выводы:

1. В данной работе было проведено исследование свойств системы  с алгоритмом адаптации на основе второго метода Ляпунова. По данным таблицы 1 были определены коэффициенты эталонного уравнения, далее вычислены элементы матрицы Н как решение уравнения Ляпунова и записаны уравнения алгоритмов адаптации с вычисленными значениями коэффициентов.

2. Стационарный объект. При r(t)=1(t), нулевых начальных условиях, =10, =1, k^r(0)=1 показатели качества переходного процесса не соответствуют требуемым.

 3. Далее были изменены значения :

При =200, =1 были обеспечены заданные показатели качества: % = 1%, t_пп = 7,7 с, t_1ппа=22 с, t_2ппа=14 с, t^r_ппа=4,7 с.

 4. Изменив начальные условия в объекте (,) также провели моделирование при =1, =1 и при =10, =1. В первом и втором случае показатели качества не удовлетворяют заданные.

5.Также изменяли последовательно параметры объекта в 2 раза(=10, =1):

а)  при a₀ = 0,2, a₁ = 0,5, b = 0,1: показатели качества являются не удовлетворительными.

б) при a₀ = 0,1, a₁ = 1, b = 0,1: показатели качества являются не удовлетворительными.

в) при a₀ = 0,1, a₁ = 0,5, b = 0,2: показатели качества являются не удовлетворительными.

Во всех случаях получили не удовлетворительные показатели качества

5. Нестационарный объект.

При нулевых начальных условиях необходимые качества процессов были получены при увеличении и  уменьшение :

а) при =1, =1 были взяты =500 =0,1 (% = 4%, t_пп = 5,8 с);

б) при =1, =10 -=150, =1 (% = 3%, t_пп = 9 с);

в) при =10, =1 - =700, =0,001 (% = 4%, t_пп = 5,4 с).

6. Наблюдатель состояния

6.1 При r(t)=1(t), нулевых начальных условиях, =10, =1, k^r(0)=1 показатели качества переходного процесса не соответствуют требуемым.

6.2 При =200, =1 были обеспечены заданные показатели качества:       % =1%, t_пп = 7,5 с, t_1ппа=22 с, t_2ппа=14 с, t^r_ппа=4,7 с

6.3

а) при =1, =1 были взяты =500 =0,1 (% = 4,5%, t_пп = 5,7 с)

б) при =1, =10 -=150, =1 (% = 3%, t_пп = 9 с);

в) при =10, =1 - =700, =0,001 показатели качества являются не удовлетворительными.

Введение наблюдателя состояния приводит к ухудшению показателей качества переходных процессов в нестационарном объекте при увеличении амплитуды.