


Петербургский Государственный Университет Путей Сообщения
кафедра “информатика и информационная безопасность ”
Лабораторная работа № 3
Выполнил ст. гр. КИБ-708
Таранин В.В.
Проверил: Еремеев М.А.
Санкт-Петербург
2010
«Генерация больших простых и псевдопростых чисел»
Формирую простое число заданного размера посредством вероятностных тестов.
Беру большое число p = 5001.
Использую тест Ферма.
Осуществляю проверку соотношения bp - 1 = 1 (mod p) в качестве параметра b использую значения от 2 до 1999.
Так уже при b = 2 bp - 1(mod p) = 4. Значит p = 5001 – составное.
Так уже при b = 2 bp - 1(mod p) = 4. Значит p = 5007 – составное
Беру следующее нечётное число p = 5003, p = 5009. Также проверяю соотношение теста Ферма при параметре b от 2 до 1999. При всех данных значениях число p проходит тест Ферма.
Для окончательной проверки данного числа на простоту, применяю тест Соловея-Штрассена. В качестве параметра x использую числа от 1 до 100. Проверяя следующее выражение:
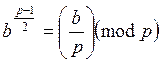
(где
![]() символ Лежандра. Для значений b являющихся
квадратичными вычетами по модулю p
символ Лежандра. Для значений b являющихся
квадратичными вычетами по модулю p 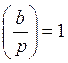 , а b = x2 mod p)
, а b = x2 mod p)
устанавливаю, что p = 1000003 – псевдопростое число с вероятностью (½)100 = 7.8*10-31
Беру третье число p = 949667 и проверяю его на простоту комбинированным способом. Для тех же условий, что и в предыдущем случае, число проходит тест Ферма. В качестве детерминированного теста использую метод пробных делений.
Необходимо
проверить делимость числа p на все числа от 2 до ![]() , т.е. от 2 до 974.
, т.е. от 2 до 974.
Проверка показывает, что число p = 949667 – простое.
«Генерация (детерминистическая) больших простых с подбором разложения функции Эйлера»
Формирую набор 10 простых чисел: (3, 5, 7, 9, 13, 15, 17, 19, 21).
Можно проверить их простоту методом пробного деления, используя программу, описанную выше, но ввиду малого размера их простота очевидна.
Из указанного набора выбираю по 3 числа. К примеру (3, 5, 7). Вычисляю число p1
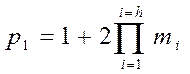
p1 = 1 + 2*(3*5*7) = 211;
Выбираю b = 2 и проверяю соотношения:
1) bp1 - 1 = 1 (mod p)
2) 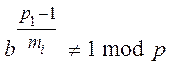 для всех mi Î {m1, m2, …, mk}.
для всех mi Î {m1, m2, …, mk}.
они выполняются, значит число 211 – простое;
Беру другой набор чисел (9, 13, 15). Выполняю ту же проверку. b = 2;
p1 = 1 + 2*(9*13*15) = 3511;
проверяю соотношения. Они выполняются, значит число 3511 – простое;
Беру другой набор чисел (17, 19, 21). Выполняю ту же проверку. b = 2;
p1 = 1 + 2*(17*19*21) = 13567
проверяю соотношения. Они выполняются, значит число 13567 – простое;
«Генерация (детерминистическая) больших простых чисел по стандарту ГОСТ Р 34.10-94»
|
P0 |
P1 |
P2 |
P3 |
|
19347 |
569 |
71 |
7 |
Для нахождения простого числа используется следующая формула:
pi - 1= piN + 1
p2 = p3N + 1 = 7*10 + 1 = 71
1) 2p3N = 1 mod p2 = 270 = 1 mod 71
2) 2N ¹ 1 mod p2 = 210 = 30 mod 71
p1 = p2N + 1 = 71*8 + 1 = 569
1) 2p2N = 1 mod p1 = 271*8 = 1 mod 569
2) 2N ¹ 1 mod p1 = 28 = 256 mod 569
p0 = p1N + 1 = 569*34 + 1 = 19347
1) 2p1N = 1 mod p0 = 2569*34 = 1 mod 19347
2) 2N ¹ 1 mod p0 = 234 = 4042 mod 19347
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.