Лабораторная работа № 4
“ИССЛЕДОВАНИЕ АЛГЕБРАИЧЕСКИХ И ВЕРОЯТНОСТНЫХ СВОЙСТВ КРИПТОГРАФИЧЕСКИХ ПРИМИТИВОВ”
Контрольное программное обеспечение:
- Программа, реализующая преобразование Уолша-Адамара: “ПУА”;
- Программа преобразования таблицы истинности булевой функции в алгебраическую нормальную форму: “АНФ”;
1. Сгенерировать случайную подстановку, осуществляющую преобразование Y=F(X) : GF(2)n® GF(2)n, для n=4, 6 или 8.
2. Определить таблицу истинности для всех БФ, реализующих подстановку: f1(X), f2(X), …, fn(X) : GF(2)n®GF(2).
3. Осуществить преобразование таблиц истинности всех БФ и их линейных комбинаций в алгебраическую нормальную форму. При выполнении данного пункта работы следует использовать программу “АНФ”.
4. Определить степень отклонений всех БФ и их линейных комбинаций от сбалансированности (количество 0 и 1).
5. Определить нелинейность и корреляционную иммунность всех БФ и их линейных комбинаций. При выполнении данного пункта работы следует использовать программу “ПУА”. Представить графически спектр Уолша-Адамара для всех БФ.
6. Найти автокорреляционную функцию всех БФ и их линейных комбинаций. Сделать вывод о выполнении критериев строгого лавинного эффекта и распространения для подстановки в целом.
7. Определить нелинейность подстановочного преобразования в целом.
8. Сделать вывод о качестве подстановочного преобразования как криптографического примитива.
1. Количественные результаты по каждому пункту работы, представленные в табличном или графическом виде.
2. Выводы по каждому пункту работы.
Приложение 1. Сведения из теории
Преобразование информации, осуществляемое криптографическими примитивами, можно формализовать в виде отображения некоторого пространства GF(2)n n-мерных векторов над полем GF(2) X = (x1, x2, …, xn) в другое пространство GF(2)m m-мерных двоичных векторов Y = (y1, y2, …, ym), где для любого iÎ{1, …, n} и любого jÎ{1, ..., m}, xiÎGF(2), yjÎGF(2). Отображения такого рода будем задавать в виде векторной булевой функции (ВБФ) Y = j(X): GF(2)n ® GF(2)m, которая является объединением компонентных БФ fi(X), осуществляющих отображение GF(2)n® GF(2), то есть j(X) ={f1(X), f2(X), …, fm(X)}.
Для описания БФ, будем использовать их представление в виде таблицы истинности и в виде алгебраической нормальной формы (АНФ). АНФ предполагает следующее описание БФ:
, (1)
где XÎGF(2)n, а все коэффициенты aÎGF(2). Таким образом, АНФ БФ над векторным пространством GF(2)n представляет собой сумму взятых с определенными коэффициентами всех возможных произведений переменных. Количество перемножаемых переменных (степень) в крайнем правом элементе АНФ является алгебраической степенью нелинейности БФ f(X) и обозначается как deg(f ).
Преобразование Уолша-Адамара
При проведении дифференциального и линейного криптоанализа, а также исследовании корреляционных свойств булевых функций (БФ), описывающих примитивы блочных алгоритмов шифрования основным аппаратом анализа является преобразование Уолша-Адамара – разновидность дискретного преобразования Фурье над конечным полем Галуа. Данное преобразование позволяет непосредственно оценить такие показатели качества БФ, как:
q сбалансированность;
q нелинейность;
q корреляционная иммунность.
Кроме того, с помощью преобразования Уолша-Адамара можно получить оценки автокорреляционных свойств БФ и различных показателей распространения изменений.
Очевидно, что БФ не могут удовлетворять всем показателям одновременно, поэтому возникает задача некоторого компромисса (оптимизации) в выборе БФ, удовлетворяющих тем или иным показателям.
Под преобразованием
Уолша-Адамара (ПУА) функции f(X), XÎGF(2)n,
относительно вектора aÎGF(2)
понимается линейное преобразование GF(2)n®Z, принимающее значение в области
действительных чисел и имеющее следующий вид:
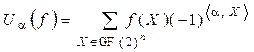(2)
где знак “
” – обозначает скалярное
произведение двух векторов.
Для сопряженной функции 
, осуществляющей отображение из GF(2)n в множество {-1, 1}, ПУА преобразуется к следующему
виду:
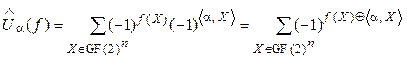. (3)
Обратное преобразование Уолша-Адамара (ОПУА) задается выражениями:
, 
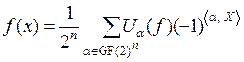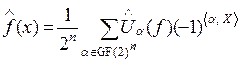. (4)
Если 2n значений таблицы истинности S(f) БФ f(X) и 2n значений действительной функции Ua(f) записать в виде вектор-столбцов [S(f)] и [Ua(f )], то линейное преобразование Уолша-Адамара задается матрицей Адамара Hn в следующем виде:
[Ua(f)] = Hn[S(f)]. (5)
Аналогично 
.
Матрица Hn формируется итеративно:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
