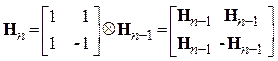Информатика и выч. техника \ Криптографические методы защиты информации

Исследование алгебраических и вероятностных свойств криптографических примитивов (Лабораторная работа № 4), страница 2

, H0 = [1],              (6)

где Ä – означает кронекеровское произведение матриц.

Кронекеровское произведение матрицы A размера m´n и матрицы B размера s´t – это матрица размера ms´nt задаваемая как

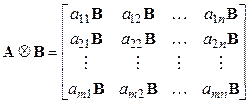,                                    (7)

где aij – элемент i-ой строки и j-го столбца матрицы A.

Если записать матрицу Адамара с помощью ее строк hi

,

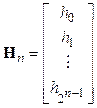то каждая строка hi матрицы Hn является характеристической последовательностью линейной функции , где вектор aiÎGF(2)n, а его целочисленное представление равно i. В свою очередь каждая характеристическая последовательность  линейной функции от n переменных является строкой матрицы Hn. Откуда следует, что строки матриц Hnи , охватывают последовательности всех аффинных функций над GF(2)n. Здесь  - матрица, все элементы которой являются инверсией элементов матрицы Hn.

Обратное ПУА описывается следующими соотношениями:

[S(f)] = 2-nHn[Ua(f)], .

Алгоритм преобразования Уолша-Адамара имеет сложность O(n2n) операций.

Сбалансированность БФ

Во избежание прямых статистических атак на примитивы криптоалгоритма необходимым условием являются:

q  сбалансированность компонентных БФ, реализующих преобразование;

q  регулярность преобразования в целом.

БФ f(X), XÎGF(2)n называется сбалансированной, если количество единиц в ее таблице истинности равно количеству нулей, т.е. #{X | f(X)=0} = #{X | f(X)=1}=2n-1.

Отображение Y=j(X) : GF(2)n®GF(2)m при n ³ m называется регулярным, если Y ровно 2n-m раза принимает все 2m различных значений из GF(2)m, в то время как X проходит 2n  значений из GF(2)n. Очевидно, что каждое регулярное отображение Y=j(X) : GF(2)n®GF(2)m при m=n является биективным отображением.

Необходимым условием регулярности отображения Y=j(X) : GF(2)n®GF(2)m при n³m является сбалансированность любых линейных комбинаций компонентных БФ, реализующих векторную БФ j(X) = {f1(X), f2(X), … , fm(X)}.

Сбалансированность БФ в терминах ПУА эквивалентна условию , , 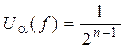где a=(0, …, 0), т.е. значение ПУА в точке “0” определяет степень отклонения БФ f(X) от сбалансированности.

Показатель сбалансированности БФ является самым простым и, как правило, рассматривается в сочетании с другими показателями.

Корреляционные свойства БФ

Существенным усилением свойства сбалансированности БФ f(X) является требование сбалансированности всех частных функций, полученных из исходной функции фиксированием любых ее k или менее переменных. Указанное требование позволяет обеспечить стойкость криптографических преобразований к статистическим атакам при фиксированных значениях битов на входе преобразования. Данное свойство связано с показателем корреляционной иммунности (КИ). При этом БФ f(X), XÎGF(2)n называется корреляционно-иммунной порядка k (CI(k)), 1£ k <n, если значение компонентов спектра УА  для всех aÎGF(2)n, вес Хэмминга которых 1 £ wt(a) £ k..

Максимальный порядок КИ БФ Y=f(X), XÎGF(2)n не превышает значения n-1. Единственными функциями, достигающими максимального порядка k=n-1 являются аффинные БФ: f(x1, x2, …, xn)=x1Åx2Å…Åxn и f(x1, x2, …, xn)=x1Åx2Å…ÅxnÅ1. Достижение максимума показателя КИ БФ является достаточно сильным требованием, поэтому введем альтернативное понятие – корреляционно-эффективных БФ, для которых не менее чем на половине векторов значения компонентов спектра УА равны 0.

Корреляционно-иммунная степени k БФ f(X) называется совершенной корреляционно-иммунной степени k или резилентной функцией, если она является сбалансированной функцией.

При синтезе БФ, обеспечивающих высокую стойкость к разностному, линейному и корреляционному  криптоанализу большое значение имеет автокорреляционная функция (АКФ) БФ. Под автокорреляцией БФ f(X) относительно вектора bÎGF(2)n понимается функция вида:

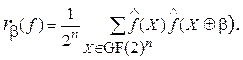                                      (8)

Существует взаимосвязь между энергетическим спектром БФ и АКФ:

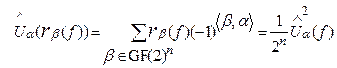, aÎGF(2)n ,                       (9)

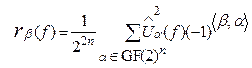, bÎGF(2)n,                             (10)

Данная взаимосвязь позволяет записывать основные показатели качества БФ в терминах АКФ.

Критерии распространения изменений для БФ

Важными характеристиками качества криптографических преобразований являются понятия критерия строгого лавинного эффекта – КСЛЭ (SAC – strict avalanche criterion) и критерия распространения – КР (PC – propagation criterion). Их основная сущность заключается в оценивание вероятности изменения значения БФ в зависимости от изменения части бит аргументов этих функций.

Пусть разность Df(X, b) = f(X)Åf(XÅb), где X, bÎGF(2)n; f(X)ÎGF(2), тогда БФ f(X) удовлетворяет:

Скачать файл