Изучение и практическое применение двухключевых блочных криптографических алгоритмов, основанных на сложности разложения целых чисел

ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ПУТЕЙ СООБЩЕНИЯ

Кафедра: «Информатика и информационная безопасность»

Лабораторная работа №2

“ИЗУЧЕНИЕ И ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ ДВУХКЛЮЧЕВЫХ БЛОЧНЫХ КРИПТОГРАФИЧЕСКИХ АЛГОРИТМОВ, ОСНОВАННЫХ НА СЛОЖНОСТИ РАЗЛОЖЕНИЯ ЦЕЛЫХ ЧИСЕЛ”

         Выполнила студент

          Группы КИБ-808

          Михейкин А.И.

Санкт-Петербург

2011

Задание 1. Генерация ключей шифрования-дешифрования:

Вариант № 9

n = 11741

p = 59

q = 199

e = 163

d = 775

φ(n) = (p - 1)(q - 1) = 11484 – функция Эйлера

Задание 2. Изучение методов шифрования – дешифрования информации

Исходный текст: РЕКА

Криптограмма y=x^e(modn), полученная с использованием алгоритма модульного возведения в степень, где x равен коду символа по таблице ASCII:

X = (208, 197, 202, 192)

Дешифрование x^’=y^d(modn):

X’ = (208, 197, 202, 192)

Вывод: Шифрование и дешифрование произведены верно, так после дешифрования получился текст, идентичный исходному, соответственно процесс шифрования и дешифрования выполняются без потерь исходной информации, что обеспечивает ее целостность.

Задание 3. Изучение методов генерации цифровой подписи и её проверки

a)  Сгенерировать цифровую подпись открытого текста x без использования хэш-функции (аналогично шифрованию, но с другим ключом) s=x^d(modn).

Исходныйтекст: РЕКА

Исходный текст в ASCII:

x1 = 208; x2 = 197; x3 = 202; x4 = 192;

Исходный текст в цифровом виде:

s1 = 8986; s2 = 6443; s3 = 5338; s4 = 518

b)  Создать подделку цифровой подписи путем возведения x и s в степень с произвольным показателем l (для его получения использовать генератор случайных чисел) x^’=x^l(modn), s^’=s^l(modn).

l = 10774 )()()()()()()()()()()

x1' = 2290; x2' = 3183; x3' = 4096; x4' = 1334; x5' = 766

s1' = 1810; s2' = 3699; s3' = 4; s4' = 2796; s5' = 1048

c)  Проверить подлинность цифровой подписи:

a=s^e(modn), проверить равенство a=x,

b=s^’e(modn), проверить равенство b=x.

При расшифровке текста, подписного подлинной цифровой подписью, получаем текст, который совпадает с исходным текстом:

a1' = 162; a2' = 165; a3' = 225; a4' = 173; a5' = 160 => a = x.

При расшифровке текста, подписного фальшивой цифровой подписью, получаем текст, который не совпадает с исходным текстом:

b1' = 2290; b2' = 3183; b3' = 4096; b4' = 1334; b5' = 766 => b ≠ x.

Цифровая подпись позволяет гарантировать подлинность передаваемых сообщений.  В данном алгоритме секретный ключ необходим для шифрования сообщения, а открытый для расшифровки. ЭЦП позволяет абоненту-получателю убедиться в том, что полученное сообщение безопасно и неизменно.

d)  Получить хэш-образ открытого текста h(x) (исходный текст тот же):

Хэш - функция h(X)=4125

e)  Получить подпись для хэш-образа s=h^d(x)(modn), используя алгоритм модульного возведения в степень.

s = 3454

f)  Создание подделки цифровой подписи путем возведения x и s в степень с произвольным показателем m (для его получения использовать генератор случайных чисел) x^’=x^m(modn), s^’=s^m(modn).

m = 4921

x' = 3790

s' = 1670

g)  Проверка подлинности цифровых подписей (x,s) и (x^’,s^’).

x = 4125

x' = 3790

Безопасность цифровой подписи открытого текста ниже, чем безопасность цифровой подписи с использованием хэш-функций, но целостность  цифровой подписи открытого текста выше целостности цифровой подписи с использованием хэш-функций, т.к. исключаются возможные потери при использовании хэш-функций. Соответственно стойкость цифровой подписи с использованием хэш-функций более надежна.

Задание 4. Изучение методов криптоанализа алгоритмов, основанных на сложности разложении целых чисел

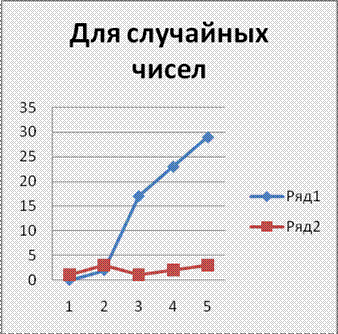
Используя алгоритм случайных чисел: число 3  Количество операций разложения - 0 множители =3 число 45  Количество операций разложения - 2 множители =3*3*5 число 347 Количество операций разложения - 17 множители =347 число 1234 Количество операций разложения - 23 множители =2*617 число 54321 Количество операций разложения - 29 множители =3*19*953

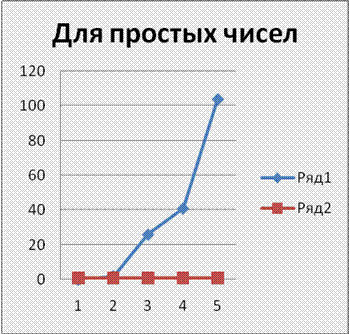
Используя алгоритм простых чисел: число 1 Количество операций разложения - 0 множители =1 число 13 Количество операций разложения - 2 множители =13  число 751 Количество операций разложения - 26 множители =751 число 1777 Количество операций разложения - 41 множители =1777 число 11113 Количество операций разложения - 104 Множители =11113

вид алгоритма	случайных чисел					простых чисел
длина числа	1	2	3	4	5	1	2	3	4	5
Количество операций разложения	0	2	17	23	29	0	2	26	41	104
количество множителей	1	3	1	2	3	1	1	1	1	1