


1. СХЕМА БЕРНУЛЛИ
2.1. ПОСЛЕДОВАТЕЛЬНОСТЬ НЕЗАВИСИМЫХ
ИСПЫТАНИЙ
Рассматривается произвольная последовательность независимых испытаний. При этом потребуем выполнения следующих условий.
1. n испытаний проводятся в совершенно одинаковых условиях;
2.
Возможным исходом каждого испытания является некоторое событие А, имеющее одну и ту же положительную, не зависящую от
номера испытания вероятность: ![]()
В
этом случае будем говорить, что имеет место последовательность испытаний
по схеме Бернулли. Ясно, что при сделанных предположениях каждая
последовательность испытаний по схеме Бернулли полностью определяется двумя
параметрами: n и p. Для удобства и
простоты записи некоторых формул введем еще одну величину: q
= 1 – p – вероятность того, что в результате данного
испытания событие А не наступит: q
=P![]() .
.
2.2. ОСНОВНЫЕ ЗАДАЧИ НА СХЕМУ БЕРНУЛЛИ
В приложениях для схемы Бернулли интерес представляют следующие вопросы, ответы на которые можно получить на основании теоремы сложения и теоремы умножения для независимых событий.
Обозначения:
![]() – число реализация события А (
– число реализация события А (![]() – число “успехов”);
– число “успехов”);
![]() вероятность того, что в последовательности n
испытаний по схеме Бернулли число “успехов” равно m;
вероятность того, что в последовательности n
испытаний по схеме Бернулли число “успехов” равно m;
![]() вероятность того, что в последовательности n
испытаний по схеме Бернулли число “успехов” меньше m.
вероятность того, что в последовательности n
испытаний по схеме Бернулли число “успехов” меньше m.
1.
![]() вероятность того, что число “успехов” равно 0.
вероятность того, что число “успехов” равно 0.
2.
![]() – вероятность того, что каждое испытание завершается “успехом”.
– вероятность того, что каждое испытание завершается “успехом”.
3.
![]() – вероятность того, что число “успехов” равно m.
– вероятность того, что число “успехов” равно m.
4.
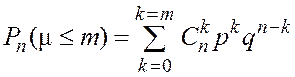 – вероятность того, что число “успехов” не меньше m.
– вероятность того, что число “успехов” не меньше m.
5.
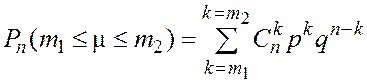 – вероятность соответствующего неравенства
– вероятность соответствующего неравенства ![]() .
.
Эти важнейшие для приложений формулы в случае большого числа n допускают приближенные выражения, основанные на трех основных предельных теоремах: локальная теорема Лапласа, интегральная теорема Лапласа, теорема Пуассона.
2.3. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ДЛЯ СХЕМЫ БЕРНУЛЛИ
Локальная теорема Лапласа. Для любого p= P(A), 0 < р < 1, справедливо предельное равенство (используются обозначения, принятые в п.2.2):
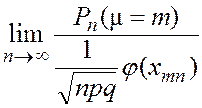 =1,
=1,
где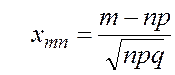 ,
, 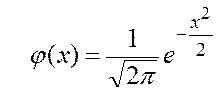 .
.
В
приложениях ценность этой теоремы определяется тем, что подсчет вероятностей ![]() можно
очень просто выполнять по следующей приближенной формуле:
можно
очень просто выполнять по следующей приближенной формуле:
![]()
![]()
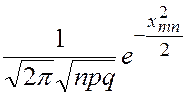 .
.
Применяя эту формулу для приближенных вычислений необходимо учитывать следующие обстоятельства.
1.
Скорость сходимости предельного
равенства не высока: порядок ее определяется как 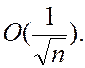 На
практике целесообразно ею пользоваться, если каждая из величин
На
практике целесообразно ею пользоваться, если каждая из величин ![]() и
и ![]() не
менее 20.
не
менее 20.
2. Следовательно, при одном и том же nболее точный результат можно получить для того значения p, которое близко к 0,5.
3. “Опасными” в смысле точности вычислений являются те критические значения p, которые близки к концам отрезка [0, 1]. Для таких значений параметра pследует пользоваться другим предельным равенством, которое составляет содержание следующей предельной теоремы о схеме Бернулли.
Теорема Пуассона. Для
серии последовательностей испытаний по схеме Бернулли, если в каждой серии
выполняется условие ![]() ,
справедливо предельное равенство
,
справедливо предельное равенство
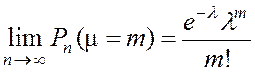 .
.
Теорему Пуассона называют теоремой о редких событиях:
условие теоремы (![]() ) предполагает,
что
) предполагает,
что 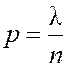 , т.е.
, т.е. 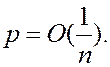
Вычисление вероятностей ![]() можно
получать по формуле
можно
получать по формуле
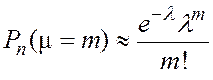 ,
,
когда величина ![]() менее 20.
менее 20.
Интегральная теорема Лапласа. Для любых ![]() и
и![]() справедливо
предельное равенство:
справедливо
предельное равенство:
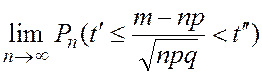 =
=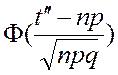 –
– 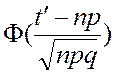 ,
,
где 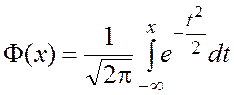 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.