ЦЕПИ МАРКОВА
1 ОДНОРОДНАЯ ЦЕПЬ МАРКОВА
Рассмотрим последовательность испытаний, таких что в результате каждого из испытаний обязательно происходит одно и только одно из k событий А1, А2, ..., Аk:
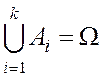 , Ai Ç Aj = Æ.
, Ai Ç Aj = Æ.
Обозначим Ai(s) событие, состоящее в том, что в результате испытания с номером s произошло событие с номером i.
О п р е д е л е н и е 1. Последовательность испытаний образует цепь Маркова, если условная вероятность события Ai(s+1) при гипотезе Aj(s) не зависит от того, какие события происходили в результате испытаний с номерами, предшествующими номеру s.
Это определение использует классические термины последовательности испытаний. Поскольку цепи Маркова в настоящее время часто применяются для описания систем, меняющих свое состояние во времени, мы приведем другое определение цепи Маркова, использующее современную терминологию.
Предположим, что некоторая система находится в одном из состояний А1, А 2, ..., Аk и может изменять свое состояние в моменты времени t1, t 2, ... , tn, ....
О п р е д е л е н и е 2. Состояние системы описывается цепью Маркова, если вероятность того, что в любой момент времени ts+1 система находится в состоянии Аi зависит от того, в каком состоянии она находилась в момент времени ts и не зависит от того, в каком состоянии эта система находилась в предыдущие моменты времени.
Обозначение: pij(s) – вероятность состояния Аi в момент времени ts+1 при условии, что в момент времени ts система находилась в состоянии Аi. Короче: вероятность перехода из состояния Аi в состояние Аj в момент времени ts.
Упрощаем модель: вероятность перехода из состояния Аi в состояние Аi не зависит от времени. Такая цепь Маркова называется однородной.
О п р е д е л е н и е 3. Цепь Маркова называется однородной, если вероятности перехода не зависят от времени:
pij(s) = pij, i,j = 1, 2, ... , k.
В дальнейшем рассматриваются только однородные цепи Маркова.
П р и м е р . Частица движется по прямой под действием случайных толчков в моменты времени t1, t 2, ... , tn, ... и может находиться в точках с целочисленными координатами 0, 1, 2, ... , N. С вероятностью р – вправо, с вероятностью q – влево. В точках 0 и N – отражающие стенки.
1 q p 1
® ¬ ® ¬
°°°°°°°°°°
1 2 3 . . . . . . . . . . . N
2 СТОХАСТИЧЕСКАЯ МАТРИЦА
Рассмотримквадратную матрицу размера k´ k:
П =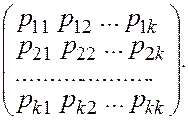
О п р е д е л е н и е . Матрица П называется стохастической, если она обладает следующими свойствами:
C1. 0 £ pij £ 1, i,j = 1, 2, ... , k.
C2. 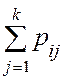 = 1.
= 1.
C3. "j, j = 1, 2, ... , k, $i: pij > 0 .
Т е о р е м а . Матрица П, элементами которой являются вероятности перехода, является стохастической.
Доказательство следует непосредственно из определения цепи Маркова и стохастической матрицы.
Такую матрицу будем называть матрицей перехода.
П р и м е р 1. Составить матрицу перехода для цепи Маркова, описанной в примере п. 3.1. Такую схему будем называть блужданием с отражением.
П =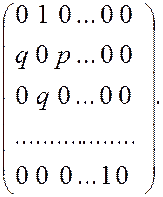
П р и м е р 2. Блуждание с поглощением.
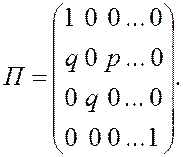
П р и м е р 3. Блуждание с отражением в центр (n=5).
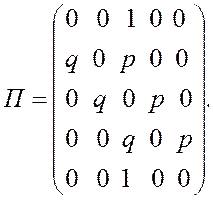
3 РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ СОСТОЯНИЙ
Предположим, что в начальный момент времени t0 система находилась в одном из состояний с вероятностями, определяемыми матрицей Р(0):
Р(0) = (p1(0), p2(0), ... , pk(0)).
Вероятности состояний через один шаг Р(1), т.е. в следующий момент времени t1, можно найти по формуле полной вероятности, если известна матрица перехода П:
![]()
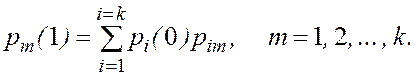
Матрица вероятностей состояний в момент времени t1 определяется по формуле:
P(1) = Р(0) П.
В свою очередь, вероятности состояний в следующий момент времени t2 могут быть определены матрицей Р(2):
P(2) = Р(1) П = Р(0) П2.
Элементы этой матрицы pij(2) – вероятности перехода из состояния iв состояние jза два шага. Матрицу П2 будем называть матрицей перехода системы за 2 шага. Аналогично вероятности состояний в момент времени tn могут быть определены с помощью матрицы Р(n):
P(n) = P(0) Пn.
Матрицу Пn можно рассматривать как матрицу перехода за nшагов. Элементы этой матрицы pij(n) – вероятности перехода из состояния iв состояние j за nшагов. Ясно, что матрица перехода за nшагов равна n-ой степени матрицы перехода за 1 шаг.
4 УРАВНЕНИЕ МАРКОВА
Полагая n = m + n , m , n Î N, записываем матрицу вероят-ностей состояний в момент времени tn:
P(m + n ) = Р(0)Пm Пn = Р(n)Пm.
Это означает, что матрица вероятностей состояний в момент времени tn, n = m+ n , равна произведению матрицы перехода за m шагов на матрицу вероятностей состояний в момент времени n.
Получаем уравнение Маркова:
pij(m + n) = ![]() pim(m)pmj(n).
pim(m)pmj(n).
P(m + n ) = Пm Р(n).
5 ТЕОРЕМА О ПРЕДЕЛЬНЫХ ВЕРОЯТНОСТЯХ
Если при некотором s все элементы матрицы перехода за s шагов положительны, то существуют такие рj, j = 1, 2, ... , k, что для всех i, i = 1, 2, ... , k, справедливо предельное равенство:
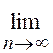 рij (n)
= pj.
рij (n)
= pj.
Физический смысл теоремы: при выполнении условий теоремы вероятность того, что система в перспективе будет находиться в состоянии с номером j, практически не зависит от того, в каком состоянии она находилась в далеком прошлом. Это свойство системы называют эргодическим.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.