Случайные величины и их распределения

4   СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

И ИХ РАСПРЕДЕЛЕНИЯ

4.1  Случайная величина

Случайной величиной называется числовая функция , которая определена в вероятностном пространстве  на множестве  такая, что для каждого числа  соответствующее множество элементарных событий , удовлетворяющих условию ,  является событием из алгебры :

.

Последнее означает, что  при  всех    для этих событий справедливы свойства алгебры событий  [1].

Если множество значений функции  есть некоторый интервал, открытый или замкнутый, конечный или бесконечный, случайная величина называется непрерывной. Если же множество значений функции  конечное или счетное, то случайная величина называется дискретной.

Для краткости событие  обозначаем , противоположное событие , пересечение событий . Случайную величину обозначают коротко одной буквой  или  .

4.2 Функция распределения

Функцией распределения случайной величины называется функция, значение которой в каждой точке , , равно вероятности события :

                                  (4.1)

С помощью функции распределения случайной величины вероятности событий  и  можно вычислить по формулам:

;                                        (4.2)

.                    (4.3)

Случайную величину дискретного типа с множеством значений  удобно определять  функцией

 .                (4.4)

Её связь с функцией распределения устанавливается  следующими формулами:

,                (4.5)

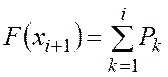.                                                        (4.6)

Таким образом, функция распределения дискретной случайной величины  есть кусочно постоянная функция.

Пример 1.          Дискретная случайная величина задана таблицей ее значений  и вероятностей , с которыми они принимаются:

i	1	2	3	4	5
	0	1	2	3	4
	0,1	0,2	0,4	0,25	0,05

Построить функцию распределения и найти вероятности событий

;     ;     .

·  В соответствии с определением функции распределения (4.1) и формулой (4.6), получаем:

      

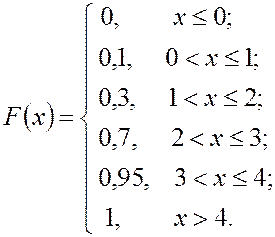
С помощью функции распределения на основании формул (4.1),  (4.2),  (4.3)  можно вычислить искомые вероятности событий:

;

;

. 

Пример 2.          Известна функция распределения случайной величины

                      

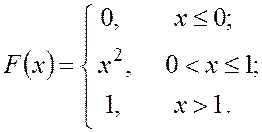
Найти вероятности событий  ;  ;  .

·  Аналогично предыдущему, получим:

;

;

. 

          Случайные  величины    называются независимыми, если при всех   выполняется равенство

.

      Это означает, что

         .

4.3  Плотность распределения

Плотностью распределения случайной величины непрерывного типа называется производная функции распределения, если она существует:

.                                         (4.7)

Если плотность распределения случайной величины известна, то функция распределения случайной величины может быть найдена по формуле:

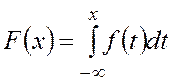.                                      (4.8)

Вероятности событий , ,  вычисляются с помощью соответствующих интегралов от плотности распределения  :

;                                       (4.9)

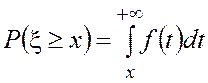;                                       (4.10)

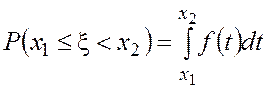.                              (4.11)

Пример 3.          Найти плотность распределения случайной величины, если известна её функция распределения

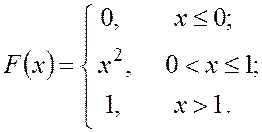
·  В соответствии с определением (4.7), для получения плотности распределения надо продифференцировать функцию распределения.

  

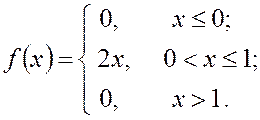
Пример 4.          Известна плотность распределения случайной величины

.

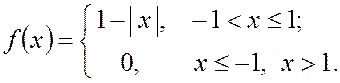Построить ее функцию распределения.

         В соответствии с выражением для плотности распределения  применим формулу (4.8), в интервалах   ,   ,   ,   :

,          ;

, ;

,          

,    .

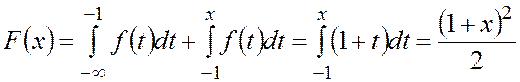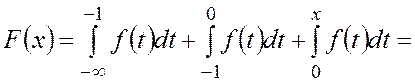
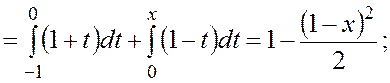
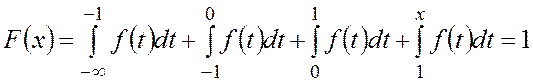Таким образом,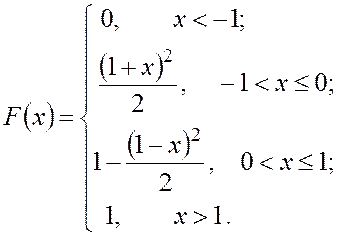        

На рис. 1 изображен график функции распределения .

                                    

1

0,5

  

-1              0                 1

                Рис.1

Пример 5.  Известна плотность распределения случайной величины

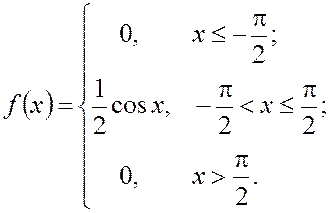
Найти вероятности событий

,, .

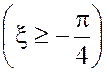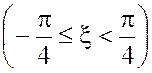·  В соответствии с формулами (4.9), (4.10), (4.11) вычисляем

вероятности этих событий:

;

;

. 

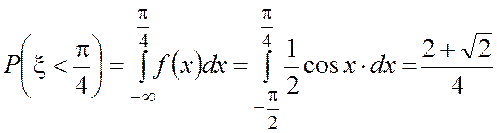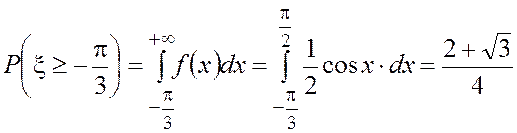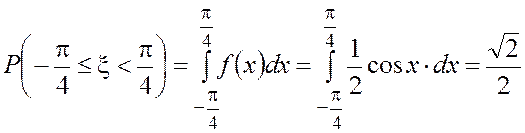4.3  Математическое ожидание

Определение математического ожидания приводится для случайных величин дискретного и непрерывного типа.

Математическим ожиданием дискретной случайной величины называется сумма произведений всевозможных значений этой случайной величины на соответствующие им вероятности:

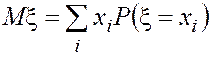.                                       (4.12)

Эта сумма в зависимости от множества значений случайной величины может быть конечной или бесконечной. В случае бесконечного множества значений математическое ожидание существует только тогда, когда сходится ряд (4.12).

Математическое ожидание непрерывной случайной величины, имеющей плотность распределения , определяется формулой

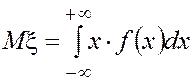   ,                                       (4.13)

если только сходится несобственный интеграл. В противном случае математического ожидания этой случайной величины не существует.

Математическое ожидание называют также средним значением случайной величины.

Пример 6.          Дискретная случайная величина задана таблицей

i	1	2	3	4	5
	0	0,2	0,4	0,6	0,8
	0,1	0,3	0,4	0,15	0,05

Найти ее математическое ожидание.

·  В соответствии с (4.12) получаем:

.

Пример 7.       Известна плотность распределения случайной величины:

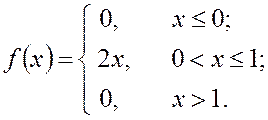
Найти ее математическое ожидание.

·  В соответствии с (4.13) получим:

           . 

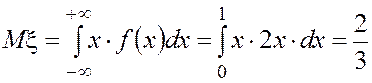4.5  Дисперсия

Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

       .                                (4.14)

Для вычисления дисперсии удобнее пользоваться формулой:

      .                                   (4.15)

Стандартным отклонением случайной величины называется квадратный корень из её дисперсии:

                  .                                          (4.16)

Пример 8.       Найти дисперсию и стандартное отклонение случайной величины из примера 6.

·  Как уже известно, . Для вычисления дисперсии применим формулу (4.15). Вычислим сначала :

Подставляя   и   в (4.15) и (4.16), получаем

;           . 

Пример 9.       Найти дисперсию и стандартное отклонение случайной величины из примера 7.

·  Математическое ожидание этой случайной величины  известно из примера 7.    Вычисляем :

 .

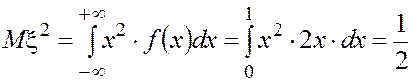Дисперсию и стандартное отклонение вычисляем по формулам (4.15) и (4.16), подставляя  ,  :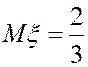

;                    . 

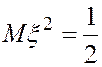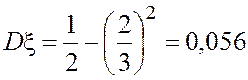4.6  Моменты

Начальным моментом -го порядка случайной величины называется математическое ожидание -ой степени этой величины:

            .                                     (4.17)

Начальный момент 1-го порядка случайной величины равен ее математическому ожиданию        .

Центральным моментом -го порядка случайной величины называется математическое ожидание -ой степени отклонения случайной величины от ее математического ожидания:

.                                  (4.18)

 Из определения следует, что центральный момент 1-го порядка равен нулю:  , центральный момент 2-го порядка  равен дисперсии:  .

Между начальными и центральными моментами имеет место зависимость:  центральные моменты выражаются через начальные. Приведем соответствующие формулы для центральных моментов 2, 3 и 4 порядков:

;                                                 (4.19)

;                                (4.20)

.              (4.21)

Пример 10.     Найти начальные и центральные моменты до 4-го порядка включительно для случайной величины из примера 6.

·  В примерах 6 и 8 вычислены , , . Вычислим по формуле (4.17) начальные моменты  и , затем по формулам (4.20), (4.21) найдем  и :

;

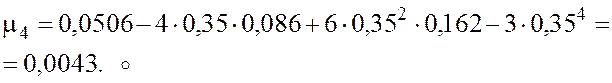
       4.7  Квантили

Пусть  – функция распределения случайной величины  непрерывного типа.

       Квантилью порядкаpраспределения случайной величины  называется корень уравнения

Иначе говоря, квантиль распределения порядка p есть число , удовлетворяющее уравнению

   .

      В приложениях иногда вероятность выражают в процентах.  В этом случае говорят о  p% -ной квантили.

      Пример 11.  Найти   квантили   и   распределения из примера 3.

·  Здесь  p полагаем последовательно равным 0,05 и 0,5:

  находим .

                тогда   .   

4.8  Нормальный закон распределения

Нормальный закон распределения случайной величины имеет функцию распределения и плотность распределения, определяемые соответственно формулами:

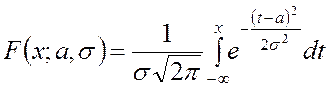;                      (4.22)

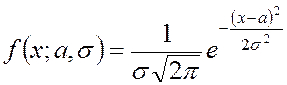.                             (4.23)

Нормальный закон имеет два параметра , , . Тот факт, что случайная величина  распределена по нормальному закону с параметрами  и , кратко обозначается . Математическое ожидание и дисперсия случайной величины, распределенной по нормальному закону , равны соответственно  и :

 

Для вычисления значения функции распределения и плотности распределения случайной величины  могут быть использованы таблицы интегральной  и дифференциальной  функций Лапласа [1], которые определяются следующими формулами:

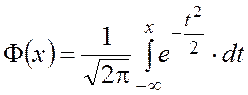;                                 (4.24)

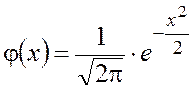.                                          (4.25)

Иногда удобнее пользоваться таблицами функции

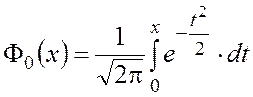,                                      (4.26)

которая является нечетной функцией и связана с функцией  равенством

.

        Таблица значений функции     приводится в приложении.

Для вычисления значений функции распределения    и плотности распределения  в (4.24) и в (4.25) заменяем  на 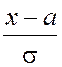 и получаем следующие выражения:

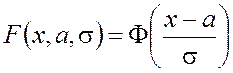;                            (4.27)

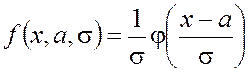.                         (4.28)

В случае нормального закона формулы  (4.1),  (4.2),  (4.3) для вероятностей событий  ,  ,   принимают следующий вид:

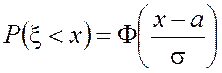;                              (4.29)

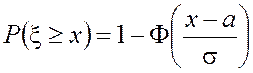;                        (4.30)

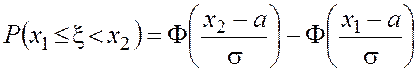.     4.31)

Особый интерес представляет отклонение случайной величины от ее среднего значения  и сравнение его со стандартным отклонением . В случае нормального закона вероятность события  зависит  от  и определяется так:

.                        (4.32)

В частности, для  (правило «трех сигм») получаем:

.

       Правило «трех сигм» означает следующее:  вероятность отклонения нормально распределенной случайной величины  от ее среднего значения  более чем на три стандартных отклонения   равна  0,003.  В зависимости  от  цены риска  можно принять  такие отклонения практически невозможными. В общем случае эти вероятности  определяются по формуле (4.320 в долях .

Пример 11.     Случайная величина распределена нормально . Найти вероятности событий , , .

·  Воспользовавшись формулами (4.29), (4.30), (4.31), получим:

.

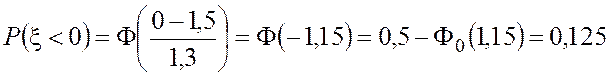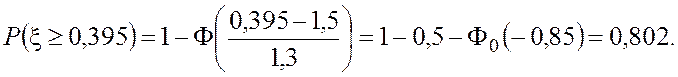
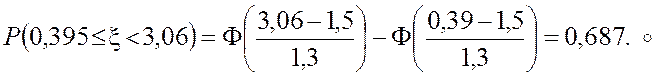
Пример 12.  Случайная величина распределена нормально . Найти вероятность события .

·  По формуле (4.32) получаем:

. 

Пример 13.  Найти интервал , соответствующий вероятности  отклонения случайной величины  от ее среднего значения.

·  Определяем  из условия . Учитывая (4.32), полагаем  и с помощью таблиц функции  находим . Это есть  квантиль случайной величины 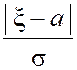   порядка .

Границы интервала  найдем, заменив неравенство  равносильным ему неравенством

.

Отсюда               ,          .

После вычислений получаем          ;      . 

4.9    Экспоненциальный закон

       Экспоненциальный закон распределения случайной величины имеет функцию распределения и плотность распределения, определяемые соответственно формулами:

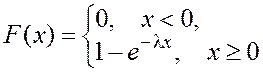                          (4.33)

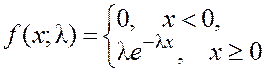                          (4.34)

      Экспоненциальный закон имеет один параметр   .

      Математическое ожидание и дисперсия равны соответственно

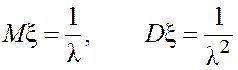.                          (4.35)

      Экспоненциальный закон обладает  следующим свойством.  Условная вероятность события     при гипотезе    зависит только от длины отрезка   и не зависит от начала отсчета этого отрезка на оси.

      Обозначение:  ~ – случайная величина    распределена по экспоненциальному закону с параметром .

                  Пример 14.  ~. Найти условную вероятность

.

·  Условная вероятность определяется по формуле [1]:

                            .

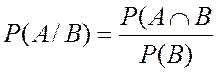В соответствии с этой формулой имеем

          .

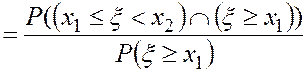·       Определяем числитель этой дроби, пользуясь свойством алгебры событий [1] и формулой  (4.11):

         

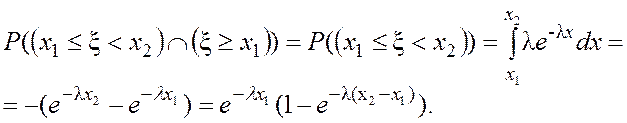
                         Знаменатель вычисляем по формуле  (4.10):

                                      .

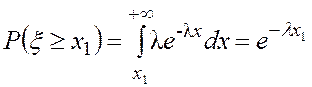 В результате получаем

      

Как видим,имеет место сдвиг аргумента:  начало отсчета переносится  в точку        

4.10Распределение максимального и минимального 

значения нескольких случайных величин

Функция распределения максимального из двух независимых случайных величин значения

имеет вид

,                        (4.36)

где   и     –  функции распределения  соответственно случайных величин  .

      Функция распределения минимального значения из двух независимых случайных величин

имеет вид

                     (4.37)

      Аналогично определяются распределения крайних значений (максимального и минимального)  из произвольного числа n  независимых случайных величин:

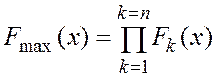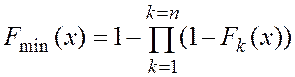,   .     (4.38)

      Распределение максимального значения из двух независимых нормально распределенных случайных величин ,   имеет вид:

.

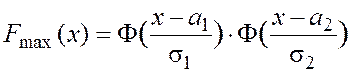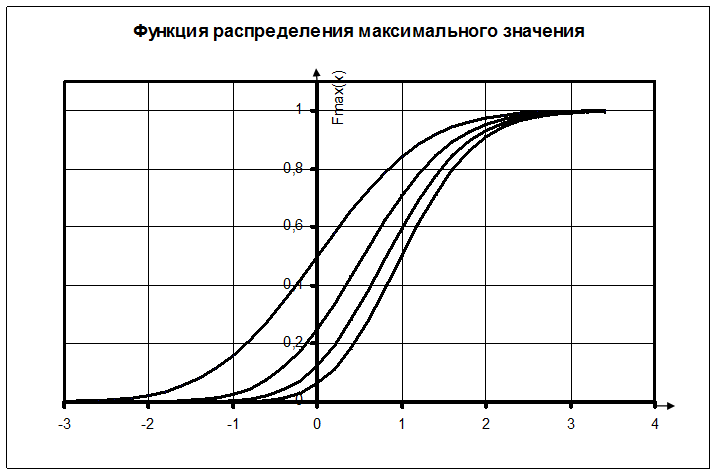Рис. 2

      На рисунке 2 приведены графики функции распределения наибольшего значения нормально распределенных случайных величин для . Квантили распределений в зависимости от числа   для разных уровней  можно приближенно найти из графиков. Более точное значение квантилей можно получить из подробных EXCEL-таблиц функций распределения. Результаты для  приведены в следующей таблице.

	1	2	3	4
	0,25	0,69	1,01	1,17

      Распределение минимального значения из двух независимых случайных величин, распределенных по экспоненциальному закону  , имеет  вид:

.

      Как видим, минимальное значение из двух случайных величин, распределенных по экспоненциальному закону, распределено по экспоненциальному закону с параметром  . Это же относится к произвольному числу независимых случайных величин