Классический подход к определению вероятности

          КЛАССИЧЕСКИЙ ПОДХОД К ОПРЕДЕЛЕНИЮ

ВЕРОЯТНОСТИ

      Предположим, что в вероятностном пространстве (W, F, P) события  А₁, А₂, ... , А_n  Î F  удовлетворяют следующим условиям:

1. 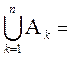 W;

2.   A_i Ç A_j = Æ;

                  3.     P(A_k) = p,   k = 1, 2, ... , n.

   Про такие события будем говорить, что они единственно возможны (условие 1), попарно несовместны (условие 2)  и  равновероятны (условие 3).

   В том же вероятностном пространстве выберем событие А Î F, эквивалентное объединению  m  событий с любыми номерами из названных выше n  событий:

А = .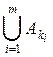

   События  , , ... ,  называются благоприятными для события А.

    Справедлива формула:

P(A) = .

   Можно содержание этой формулы выразить следующей формулировкой.

   Вероятность события равна отношению числа mблагоприятных ему событий к их общему числу nединственно возможных, попарно несовместных и равновероятных событий.

Доказательство. Из условия 1 следует, что

Р 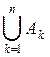 () = Р(W) = 1.

   С другой стороны, из условий 2 и  3 следует

Р 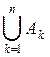 () =  Р(А_k)  = np.

   Следовательно, 

р = 1/n.

Снова используя условия 2 и 3, получаем

Р(А) = Р ( 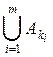) = Р() = mp = ,

что и требовалось доказать.

          Как видим, классический подход к вычислению вероятностей по формуле P(A) =   выведен из аксиоматического определения вероятностей.  Определением вероятности события такой подход считать нельзя, поскольку он исходит из предположения P(A_k) = p,   k = 1, 2, ... , n, т.е. использует понятие вероятности (логически не допустимо).

          Однако  этот подход вполне оправдан для вычисления вероятностей событий, заданных на конечном множестве равновероятных событий. В этом случае говорят, что задано равномерное распределение вероятностей на конечном множестве событий.

          Пример.

1.6.  ГЕОМЕТРИЧЕСКИЙ ПОДХОД К ОПРЕДЕЛЕНИЮ ВЕРОЯТНОСТИ

      Выберем в качестве пространства элементарных событий мно-жество точек из отрезка [a, b]. Элементарными событиями будут все возможные точки х, х Î [a, b], а событиями – интервалы и отрезки, содержащиеся в [a, b]. Положим вероятность каждого такого события пропорциональной длине соответствующего отрезка или интервала:

P (х Î [a, b]) = k (b - a).

      Естественно (А2 вероятностного пространства), что

Р(х Î [a, b]) = Р(W) = 1.

С другой стороны, та же вероятность пропорциональна длине отрезка:

Р (х Î [a, b])  =  k (b – a).

Поэтому   k = 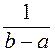,  и  получаем для любых  a, b Î [a, b]

P (х Î [a, b])   = .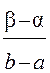

      То же справедливо для любого интервала, открытого или полуоткрытого.

      В этом случае, когда вероятность принимается пропорциональ-ной длине отрезка, говорят, что задано равномерное распределение вероятности на отрезке  [a, b].

      Аналогично  вводится равномерное распределение вероятности в некоторой заданной области W на плоскости.    В этом случае вероятность события А вводится как отношение соответствующих площадей:

P (A) = .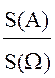

      Выбирая  в качестве пространства элементарных событий множество точек в определенной области W в трехмерном пространстве, можно ввести равномерное распределение вероятностей в этой области как отношение объемов:

P (A) = .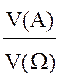

       П р и м е р 1. Задача о вещественных корнях квадратного трехчлена.

      П р и м е р 2. Задача о встрече.