






Федеральное агентство образования Российской Федерации
Санкт-Петербургский государственный горный институт им. Г.В. Плеханова
(технический университет)
Кафедра высшей математики
11 вариант
По дисциплине: Высшая математика .
(наименование дисциплины согласно учебному плану)
Автор: студент гр. ЭГ-03 ______________ /Шульгина Е. Д,/
(подпись) (Ф.И.О.)
ОЦЕНКА: _____________
Дата: ___________________
ПРОВЕРИЛ: Доцент ________________ /Лебедев И.А./
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2004 год
Задание 1
По шифру ![]() определяем исходные данные:
определяем исходные данные:
![]()
![]()
![]()
![]()
Возьмем за x1 количество
произведенного товара A, а за x2
количество товара B, тогда ![]() –
план, а целевой функцией является прибыль от продажи обоих товаров:
–
план, а целевой функцией является прибыль от продажи обоих товаров: ![]()
Сначала решим задачу геометрическим методом.
Для этого сперва надо найти градиент для данной функции: ![]() .
.
После этого составляем неравенства ограничений:
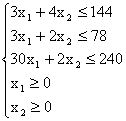
![]()
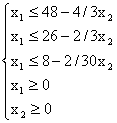 или
или 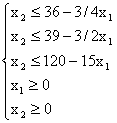
Подставим в каждое из этих неравенств начало координат для определения нужных полуплоскостей. Таким образом, получаем многоугольник, заштрихованный на чертеже. Двигаясь по графику в направлении градиента, мы получаем точку пересечения ребер симплекса (вершину этого симплекса). Для определения ее координат составляем систему уравнений:
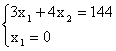
Решая ее, получаем координаты вершины симплекса, являющиеся оптимальным планом для данной функции
![]()
![]()
![]()
![]()
![]()
Теперь решим задачу симплексным методом.
Для этого необходимо привести ее к каноническому виду, т.е. задачу
максимизации сделать задачей минимизации ![]()
![]()
![]() ,
а в матрице ограничений в неравенства надо добавить балансовые переменные для
превращения неравенств в уравнения:
,
а в матрице ограничений в неравенства надо добавить балансовые переменные для
превращения неравенств в уравнения:

![]()
![]()
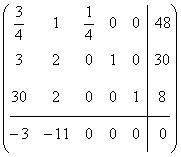
![]()
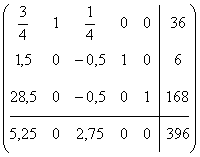
Получаем план ![]() . Так как все коэффициенты
. Так как все коэффициенты ![]() при свободных переменных (x1 и x3)
неотрицательны, то получаем план
при свободных переменных (x1 и x3)
неотрицательны, то получаем план ![]() , который является
оптимальным; так как при свободных переменных (x1 и
x3) нет коэффициентов
, который является
оптимальным; так как при свободных переменных (x1 и
x3) нет коэффициентов ![]() , равных нулю, план единственный, а
значение целевой функции при нем равно:
, равных нулю, план единственный, а
значение целевой функции при нем равно: ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.