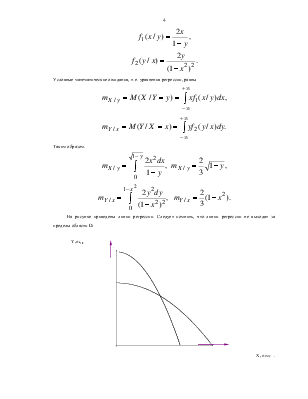
Решение типовых задач по теме: "Регрессионный анализ"

Решение типовых задач

Пример 1. Дана система двух дискретных случайных величин

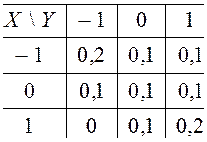
Найти числовые характеристики отдельных величин, коэффициент корреляции, если он равен нулю, исследовать величины на независимость, а если нет, то объяснить, что это означает и найти условные математические ожидания.

Решение.  Сначала найдем безусловные распределения величин

X и Y.

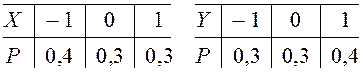
Напомним, что вероятности равны суммам соответствующих строк (столбцов) исходной таблицы, т. е.

или

Зная эти распределения, находим

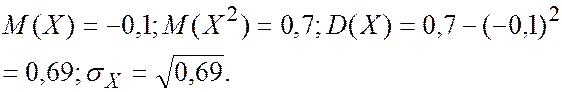
Для нахождения коэффициента корреляции по исходной таблице найдем M(XY) по формуле

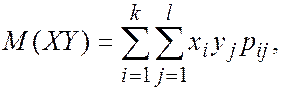
то есть

Тогда коэффициент корреляции находится по формуле

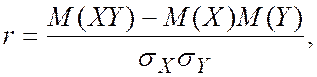
то есть

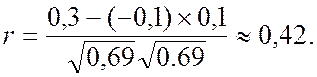
Коэффициент детерминации, %,  равен

Величины X и Y - коррелированы, с возрастанием одной величины другая имеет тенденцию к возрастанию (так как r > 0), 17,64 % вариации (изменения, колебания) одной величины вызвано линейным (главным) влиянием другой.

Теперь найдем условные математические ожидания. Напомним формулу для вычисления

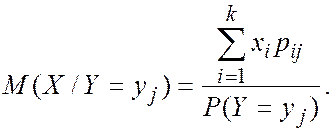
Например,

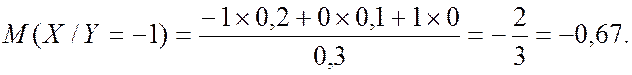
Аналогично

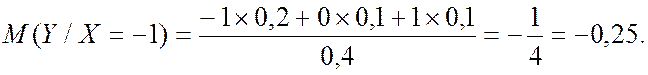
Значения условных математических ожиданий приведены в таблицах:

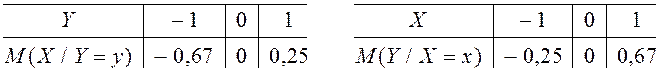
Пример 2. Исследовать систему случайных величин (X,Y):

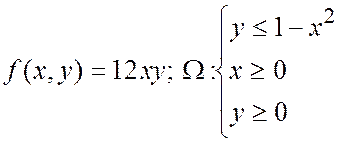
Графическое изображение области W и объяснение расстановки пределов интегрирования предоставляется читателю.

Найдем плотности отдельных величин

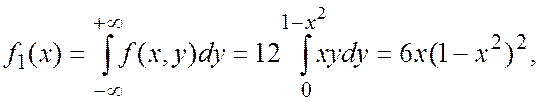
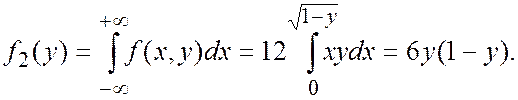
Числовые характеристики величин составляющих систему равны

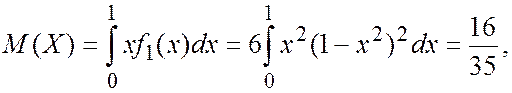
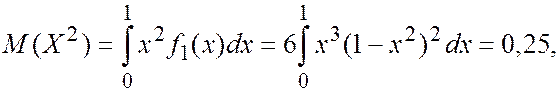
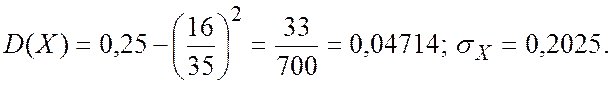
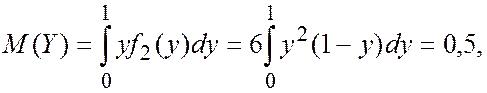
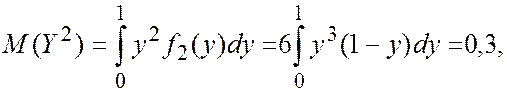
Теперь вычислим коэффициент корреляции, для чего найдем

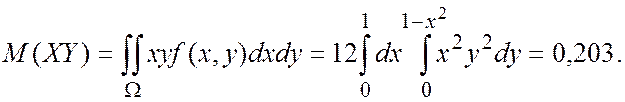
Тогда коэффициент корреляции равен

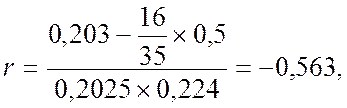
а коэффициент детерминации, %

Таким образом, случайные величины коррелированы, с возрастанием одной другая имеет тенденцию к убыванию (так как r<0) и более 31 % вариации одной величины вызвано линейным (главным) влиянием другой.

Найдем условные плотности и уравнения регрессии. Условные плотности равны соответственно

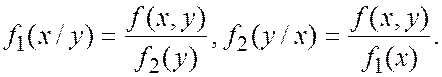
Поэтому

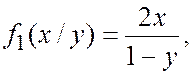
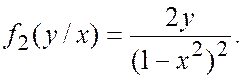
Условные математические ожидания, т. е. уравнения регрессии, равны

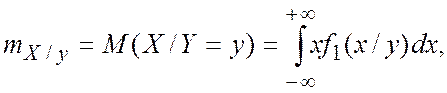
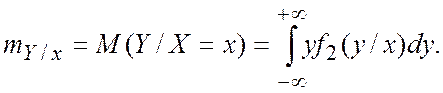
Таким образом.

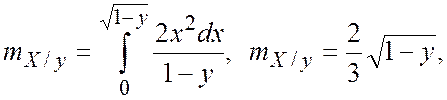
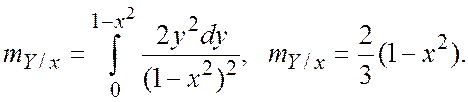
На рисунке приведены линии регрессии. Следует помнить, что линии регрессии не выходят за пределы области W.

               Y,m_Y\x

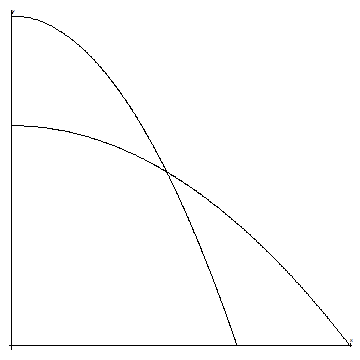
 X, m_X\y   .

Пример 3. В таблице приведена выборка объема n = 100. Приведены пары значений системы (X,Y) и частоты соответствующих пар. Найти оценки математических ожиданий, дисперсий и коэффициента корреляции. Проверить значимость коэффициента корреляции при уровне значимости 0,05.

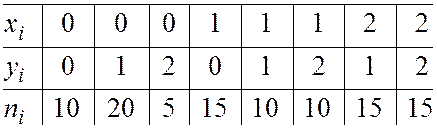
Напомним, что оценки математического ожидания и дисперсии находятся по формулам

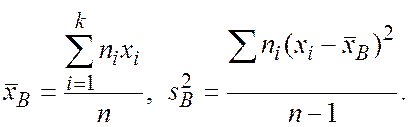
В нашем случае k - это число различных пар, поэтому k = 8. После расчетов мы получаем

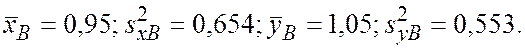
Оценка коэффициента корреляции для выборки в форме приведенной таблицы вычисляется по формуле

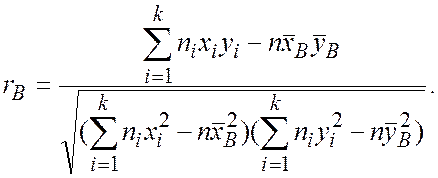
Легко сосчитать

Поэтому коэффициент корреляции равен

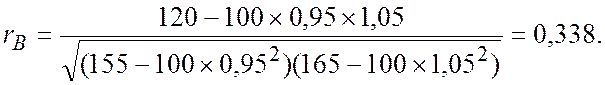
Значимость коэффициента корреляции можно проверять по двум критериям. Первый из них определяет значимые коэффициенты, удовлетворяющие неравенству

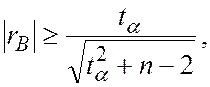
где n - объем выборки,

     - параметр Стьюдента с числом степеней свободы n - 2 и уровнем значимости a.

Отметим, что при больших выборках (практически при n > 30), можно считать

Этот критерий определяет границу значимости для всех оценок,

найденных по выборке объема 100. В нашем случае критерий значимости имеет вид

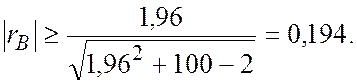
Так как 0,338 > 0,194, то коэффициент корреляции значим при уровне значимости 0,05.

Второй критерий определяет границы для каждой оценки отдельно. По найденной оценке коэффициента корреляции определяется среднее квадратичное отклонение этой оценки по формуле

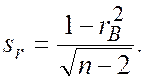
Коэффициент корреляции является значимым при уровне значимости a, если

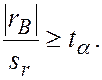
В нашем случае

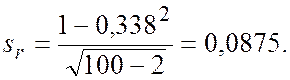
Так как

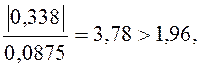
то и по этому критерия коэффициент корреляции значим при уровне значимости 0,05.

ЗАДАЧА 4 (31-40)

В табл. приведен план эксперимента с двумя факторами. Факторы изменяются на трех уровнях.

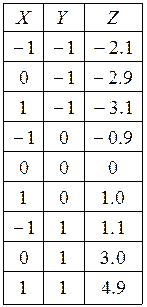
Найти коэффициенты средней квадратической регрессии вида z=b₁x+b₂xy+b₃y. Проверить адекватность полученной регрессионной модели по значимости коэффициента корреляции между расчетными и фактически­ми значениями коэффициента корреляции при уровне значимости α=0,05.

Можно рассматривать X и Y как значения некоторых факторов эксперимента (аргументов), а  Z как отклик на изменения этих факторов, т.е. функцию. Обратим внимание, что при X=Y=0 Z=0,т.е. можно рассматривать без свободного члена (b=0). Так как коэффициенты b_i (i=0,3) определяются как аргументы минимума функции