Решение типовых задач по теме: "Регрессионный анализ", страница 2

то для нахождения оценок коэффициентов b_i следует минимизировать оценку математического ожидания, т.е. среднее значение.

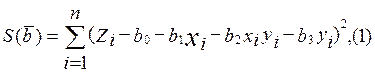 где n– объем выборки.

Чтобы найти минимум (1), надо приравнять нулю частные производные:

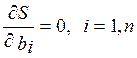. Получим систему нормальных уравнений метода наименьших квадратов.

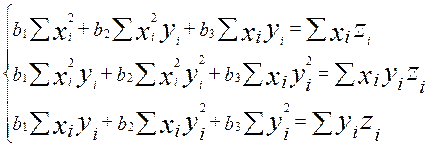
Система имеет следующее решение:

Введём матрицу, столбцы которой определяются видом уравнения регрессии: столбец состоит из тех значений элементов выборки, на которые умножается коэффициент регрессии с этим номером. При этом свободный член умножается на 1. Число строк матрицы равно объему выборки. Так, для уравнения   z=b₁x+b₂xy+b₃y первый коэффициент умножается на x , следовательно, в первом столбце стоят значения x_i, а второй коэффициент умножается на xy – во втором столбце стоят произведения x_iy_i и соответственно в третьем столбце  столбце y_i.  Матрица будет иметь следующий вид: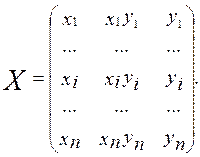 Введем  матрицу – столбец отклика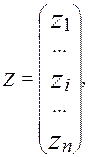  и матрицу – столбец неизвестных параметров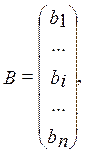

Тогда система нормальных уравнений МНК примет следующий вид:

Для условий задачи заполним матрицу X и транспонированную X^T.

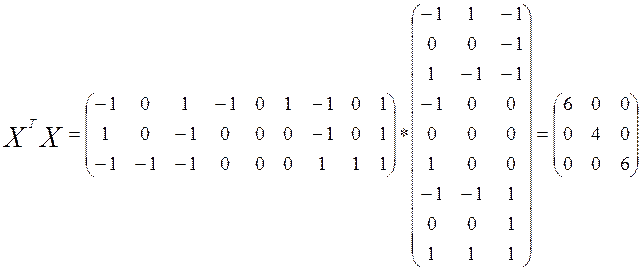
Очевидно, что обратная матрица будет также диагональной, причем на главной диагонали будут стоять обратные числа, т.е.

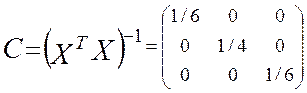
В табл. П9 приведены фактические и расчетные по уравнению z = 0,783x + 1,200xy + 2,850y значения функции z , обозначенные Z_ф и Z_р соответственно. Фактические значения. Тогда сумма квадратов отклонений расчетных от фактических значений будет равна S = 0,2791. n = 9, l = 3 и v = 9 – 3 =  6. Для уровня значимости 0,05 и числа степеней свободы равной v = 6 (n – объем выборки; l - число оценок коэффициентов регрессии; v = n - l) по таблицам распределения Стьюдента находим t_0,05 = 2,447.

Таблица П9 (Z_ф - Z_р)²

Для оценки значимости коэффициентов регрессии определим для

каждого коэффициента b_i случайную ошибку

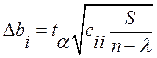
где с_ii – i-й диагональный элемент матрицы С;

S – сумма квадратов отклонений расчетных значений y от фактических;

n – объем выборки;

l - число оценок коэффициентов регрессии;

t_a - параметр Стьюдента, найденный по таблицам по уровню значимости a и числу степеней свободы        v = n - l.

 Критерий значимости, т.е. проверка нулевой гипотезы Н₀: b_i = 0, состоит в следующем: если , то коэффициент регрессии значим, т.е. гипотеза Н₀ отвергается, в противном случае нет оснований отвергнуть гипотезу Н₀ и коэффициент регрессии незначим, т.е. его можно в уравнении считать равным нулю. При этом можно сказать, что с надежностью 1-a

                                  (18.2)

Тогда

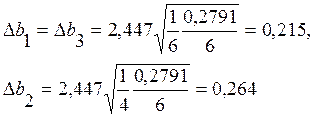
и можно утверждать, что все три коэффициента значимы при уровне значимости 0,05, и записать, что

 и

с надежностью 1 – 0,05 = 0,95.

ЗАДАЧА 5 (41-50)

Пример 10. Дана выборка объема n = 6 системы случайных величин (X, Y, Z): (1; 1; -1,1), (2; 1; 0,9), (3; 3; -3,1), (1; 2; -4,1), (2; 2; -2,9), (3; 1; 3,1). Найти и исследовать линейное уравнение средней квадратической регрессии z = a₀ + a₁x + a₂y. Найти матрицу парных коэффициентов корреляции и вектор множественных коэффициентов корреляции. Указать значимые коэффициенты при уровне значимости α=0,05. Очевидно, система нормальных уравнений имеет вид:

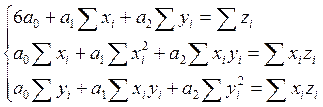
Для вычислений коэффициентов этой системы составим табл. П10, в последней строке которой приведены соответствующие суммы.

Таблица П10 X²