Силовой расчёт механизмов с учетом трения в КП

18 Силовой расчёт механизмов с учетом трения в КП. Решение нелинейных..

Система уравнений кинетостатики для ползуна:

–R₂₃cosα + (P + Ф₃) + fR₀₃signR₀₃ = 0,

R₂₃sinα + R₀₃ – G₃ = 0,                                                

–R₀₃a + fR₀₃h = 0.

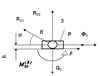
Здесь а – расстояние от оси шарнира В до линии действия силы реакции , 

выразим R₂₃:

Подставляя R₂₃ в первое уравнение :

Вариант 1.2. «Большое» трение; рабочая нагрузка P и сила инерции Ф₃ направлены против скорости ползуна. Уравнение (5.26) не имеет решения. Действительно, положив  R₀₃ > 0 (signR₀₃ = + 1), получим ,

т.к. числитель дроби отрицательный, а знаменатель – положительный. При R₀₃<0 (signR₀₃ = – 1) имеем , поскольку числитель и знаменатель дроби отрицательные. Получающееся противоречие показывает, что решения не существует. Этот случай соответствует режиму самоторможения, при котором в рассматриваемом положении механизма и при заданном направлении силы движение вообще становится невозможным.

Вариант 2.2. «Большое» трение; силы Pи Ф₃ направлены против оси х («помогают» движению ползуна). Тогда уравнение (5.26) имеет два решения. Действительно, полагая, что R₀₃ > 0 (signR₀₃ = + 1), имеем:

,

поскольку числитель и знаменатель дроби положительные. Положив R₀₃ < 0 (signR₀₃ = – 1), получаем второе решение , поскольку числитель положительный, а знаменатель отрицательный. В этом случае мы имеем дело с режимом оттормаживания: при «большом» трении движение возможно в том случае, когда вектор Р + Ф₃ направлен так же, как и скорость ползуна. Существование двух режимов оттормаживания является одним из парадоксов Кулонова трения, подробно исследованных в книге Пенлеве[1]. Установить, какое из решений будет фактически осуществляться, строго говоря, в рамках модели механизма с жесткими звеньями невозможно. Можно только показать, что некоторые «физические» соображения свидетельствуют в пользу первого решения. Нетрудно понять, что при увеличении коэффициента трения f следует ожидать увеличения модуля силы трения |F| , т.е. должно быть d|F|/df>0.  Исследуя первое решение, получаем

,

поскольку G₃ctgα – (P + Ф₃) > 0. Следовательно,

.

Для второго решения находим

,

поскольку ctgα – f < 0. Следовательно,

.

Поэтому второе решение является с физической точки зрения «недостоверным».

Сведем все найденные решения в табл. 5.4. Для удобства сравнения результатов, полученных двумя методами, разделим числитель и знаменатель дроби выражения (5.26) на ctgα.