Выбор и обоснование кинематической схемы зубодолбежного станка

результатам геометрического и кинематического анализа прототипов выбираем один прототип и для него производим силовой расчёт, выбираем двигатель и проводим кинематическое исследование машинного агрегата.

I.2 Исходные данные

В качестве исходных данных заданы технические характеристики механизма:

·  Длина зуба нарезаемого колеса 0.06 м,

·  Коэффициент изменения средней скорости  ,

·  Число оборотов кривошипа ,

·  Максимальная сила резания

·  Перебег резца

Массы звеньев  , где погонная масса .

Коэффициент неравномерности .

Радиус долбяка равен длине кривошипа.

Кроме того, задана индикаторная диаграмма, показывающая зависимость величины усилия на рабочее звено от хода рабочего звена.

 

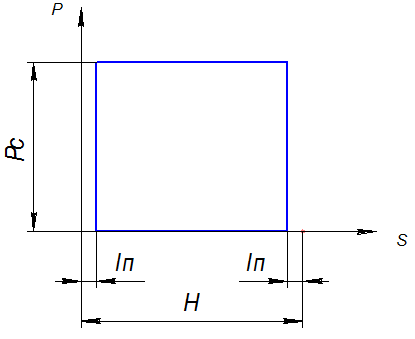Рис.I.1. Индикаторная диаграмма.

I.3 Описание работы машины

При нарезании блочных колес и колес с буртами, колес с внутренними зубьями, зубчатых секторов обработка зубодолблением является единственно возможным методом обработки. Во всех других случаях выбор метода обработки зубчатых колес подтверждается технико-экономическим расчетом.

Зубчатые колёса долбят на специальных зубодолбёжных станках с применением специальных долбяков. Зубодолбёжный долбяк представляет из себя зубчатое колесо, снабжённое режущими кромками. Поскольку срезать сразу весь слой металла обычно невозможно, обработка производится в несколько этапов. При обработке инструмент совершает возвратно-поступательное движение относительно заготовки. После каждого двойного хода, заготовка и инструмент поворачиваются относительно своих осей. Таким образом, инструмент и заготовка как бы "обкатываются" друг по другу. После того, как заготовка сделает полный оборот, долбяк соврешает движение подачи к заготовке. Этот процесс происходит до тех пор, пока не будет удалён весь необходимый слой металла.

Для создания движения резания долбяк получает возвратно-поступательное движение в направлении, параллельном оси обрабатываемого колеса. Скорость перемещения долбяка является скоростью резания.

I.4 Выбор критериев синтеза исполнительного механизма

            Для того , чтобы спроектировать механизм, необходимо сначала выбрать прототип будущего зубодолбежного станка, а затем провести синтез по выбранным критериям с целью получения механизма, соответствующего техническому заданию. В качестве критериев синтеза выберем следующее:

1)  Максимальный ход рабочего звена  .

Данный критерий определяется разностью максимального и минимального  положений  рабочего звена (в данном случае левого и правого).

2)   

Критерий, характеризующий внешние условия передачи сил в механизме;

3)   

Критерий, характеризующий внутренние условия передачи сил в механизме.

4) 

Коэффициент изменения средней скорости. Определяется, как отношение рабочего хода к холостому.

5)  Габариты механизма.

II. Прототипы исполнительного механизма

II.1 Описание прототипов

II.1.1 Структурный анализ некулисного механизма (прототип 1)

            Целью структурного анализа механизма является определение количества звеньев и кинематических пар, классификация последних, определение подвижности пар и степени подвижности механизма, а также выделение в нем структурных групп -кинематических цепей, у которых число входов совпадает с числом степеней подвижности.

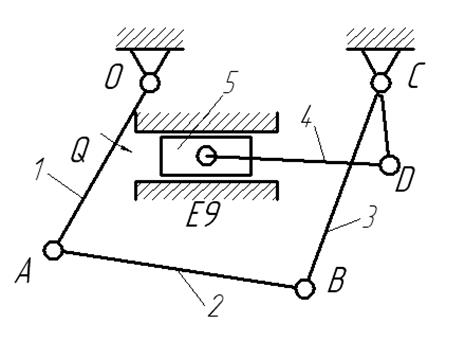
Рис.II.1. Кинематическая схема механизма.

II.1.2 Структурный анализ кулисного механизма (прототип 2)

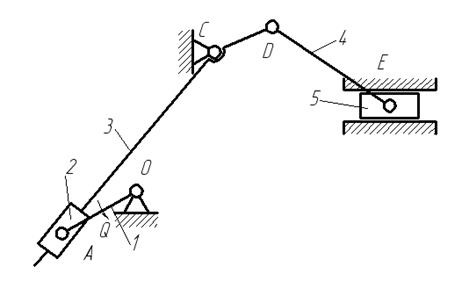
Рис.II.2. Кинематическая схема механизма.

Структурный анализ механизмов смотрите в курсовой работе «Кинематический и силовой анализ рычажных механизмов».

II.2 Выбор геометрических параметров прототипов

            Выбраны следующие размеры:

Таблица II.1

II.3 Сравнение прототипов по выбранным критериям

Для сравнения прототипов воспользуемся следующими критериями синтеза:

Габаритный размер.

Для определения габаритных размеров построим планы 12-ти положений (их схематическое изображение приведено в приложении 1, а точный вид в масштабе - на первом листе А1). Длину определяем как разницу между максимальным и минимальным значениями координаты X, а высоту как разницу между максимальным и минимальным значениями координаты Y.

Максимальный ход рабочего звена. (Hmax)

Коэффициент К1.

Характеризует внешние условия передачи сил

,где  - аналог скорости ползуна,

        - длина кривошипа.

Обычно .

Коэффициент К2.

Характеризует относительный уровень реакций в механизме

,где  – величина угла давления.

Обычно

Коэффициент Кv.

            Коэффициент изменения средней скорости. Определяется как отношение рабочего хода к холостому.

Чем меньше эти коэффициенты, тем лучше механизм.

Составим таблицу сравнения:

Таблица II.2

II.4 Выводы

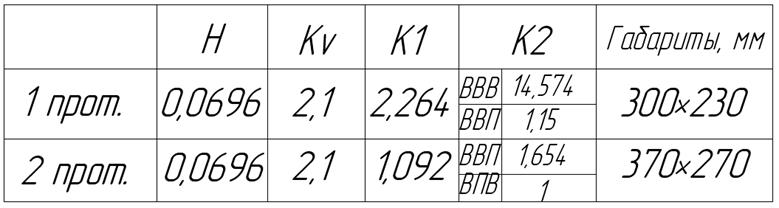
            В результате сравнения прототипов по выбранным критериям можно сделать первоначальные выводы о том, какой из прототипов более подходит. Габариты у  первого прототипа меньше, но зато коэффициенты K1 и K2 меньше у второго прототипа, следовательно прототип второй наиболее приемлем для дальнейших расчетов.

III. Геометрический анализ механизмов

Целью геометрического анализа рычажного механизма является составление уравнений геометрического анализа,  решение их,  выделение побочных и основных решений, определяющих положения звеньев, а  также исследование функций положения  выходных  звеньев структурных групп.

III.1 Составление и решение уравнений геометрического анализа

Целью геометрического анализа является определение функций положения механизма – зависимостей выходных координат, определяющих положения его звеньев, от заданных входных координат.

III.1.1 Некулисный механизм (прототип 1)

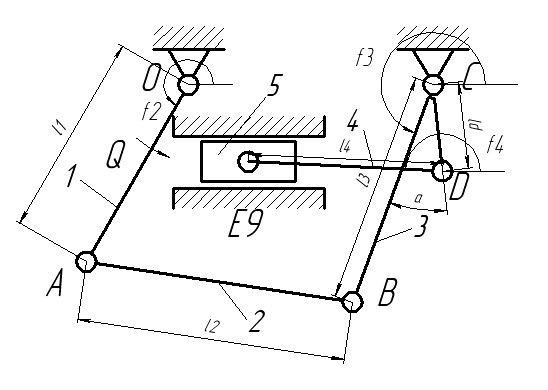
Рис.III.1. Кинематическая схема механизма.

Групповые уравнения и их решение

Уравнения геометрического анализа.

Кривошип:                            

1-я группа ВВП:                    

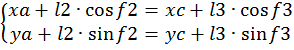
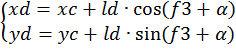
2-я группа ВВП:                    

III.1 .2 Кулисный механизм (прототип 2)

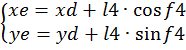
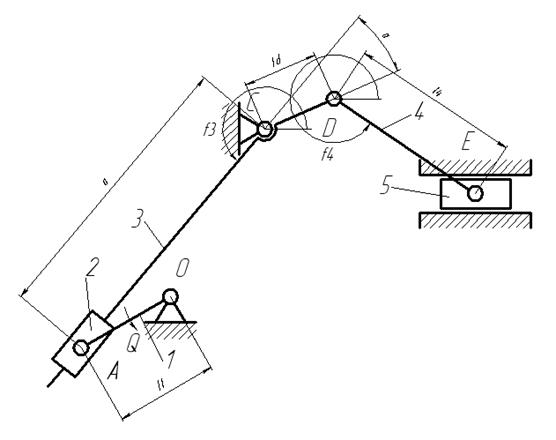
Рис.III.2. Кинематическая схема механизма.

Групповые уравнения и их решение

Уравнения геометрического анализа.

Кривошип:                 

Система не имеет неизвестных, так как координаты точки А полностью определяются за счет входной координаты q.

1-я группа ВВП:         

2-я группа ВВП:

Решение групповых уравнений и нахождение соответствующих углов смотрите в приложении-1 в MathCAD.

III.2 Выводы

            В результате геометрического анализа механизма были найдены линейные