


Санкт-петербургский государственный политехнический университет
Кафедра
Информационные машиностроительные технологии.
Отчет по лабораторной работе № 10
студент: Анищук С.Н.
группа: 2045/1
преподаватель: Щенев В.В.
Санкт-Петербург
2009г.
Цель: изучение численных методов решения обыкновенных дифференциальных уравнений первого порядка.
Задание :
1. Вычисление общих параметров.
|
|
Определяем функцию f(x,y) правой части уравнения
|
|
|
|
Задаем границы отрезка. На котором будем искать численное решение
|
|
Произвольно задаем количество интервалов
|
|
Определяем шаг интегрирования
|
|
|
|
|
|
Задаем аргумент для точного решения
Записываем функцию точного решения ОДУ
Задаем начальное значение переменной x
|
|
Определяем формулу для вычисления аргументов узлов.
|
|
2. Метод Эйлера (метод ломаных)
|
|
|
|
|
|
|
|
|
|
Задаем и проверяем правильность записи начального
значения искомого решения ОДУ согласно
формулировке условий задачи Коши
Вычисляем значения численного решения ОДУ согласно
методу Эйлера
Определяем абсолютную погрешность в узлах
промежутка
|
|
|
|
Определяем максимальную абсолютную и относительную погрешность в последнем узле
3. Первый модифицированный метод Эйлера (усовершенствованный)
|
|
Задаем начальные условия для задачи Коши
Записываем первую формулу для модифицированного
метода Эйлера:
|
|
|
|
Определяем абсолютную погрешность в узлах промежутка
|
|
|
|
Определяем максимальную абсолютную и относительную
погрешность в последнем узле
![]() %
%
4. Второй модифицированный метод Эйлера (исправленный)
|
|
|
|
|
|
|
|
|
|
Задаем начальные условия для задачи Коши
Записываем вторую формулу для модифицированного метода Эйлера:
|
|
Определяем абсолютную погрешность в узлах промежутка
Определяем максимальную абсолютную и относительную погрешность в последнем узле
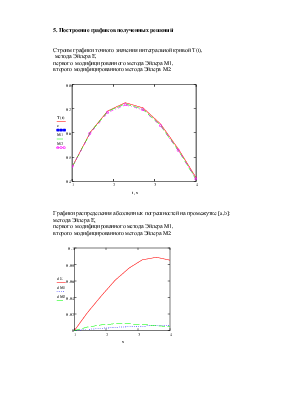
5. Построение графиков полученных решений
Строим графики точного значения интегральной кривой T(t),
метода Эйлера Е,
первого модифицированного метода Эйлера M1,
второго модифицированного метода Эйлера M2:
|
|
Графики распределения абсолютных погрешностей на промежутке [a,b]:
метода Эйлера Е,
первого модифицированного метода Эйлера M1,
второго модифицированного метода Эйлера M2:
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.