Расчет корреляционной связи между случайными величинами X и Y. Выбор лучшей модели по критерию Уилкса

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский

государственный политехнический университет»

Институт металлургии, машиностроения и транспорта

Кафедра «Машины и технология обработки металлов давлением»

Отчёт

по расчетному заданию № 2

Студенты гр. 43321/1                                            Емельянов А.С.

                 Преподаватель                                                      Востров В. Н.

"___"_______________ 2013г.

Санкт-Петербург

2013

Задание

1)  Оценить корреляционную связь между случайными величинами  X и Y;

2)  Построить регрессионные модели:

а) линейная модель;

б) квадратичная модель;

в) степенная модель;

3)  Сравнить качество моделей (тремя методами) и выбрать лучшую;

4)  Изобразить модели графически.

Исходные данные

Вариант №8

Таблица 1

Оценка корреляционной связи между случайными величинами  X и Y

Генеральное среднее совокупности случайных величин:

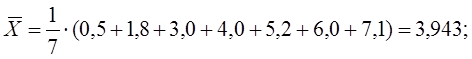
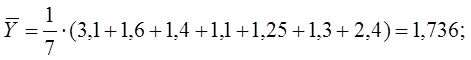
Средние квадратов:

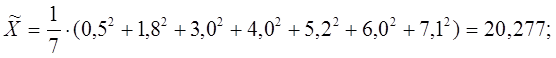
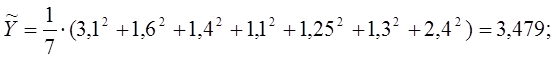
Эмпирическая ковариация совокупностей случайных величин Х и Y:

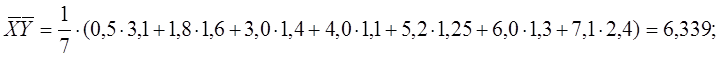
Ковариация совокупностей случайных величин Х и Y:

Среднеквадратичное отклонение совокупности случайных величин:

Коэффициент корреляции случайных величин  X и Y:

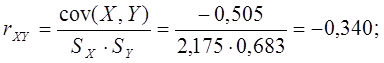
Так как коэффициент корреляции r_XY  равен -0,340, то можно сделать вывод, что случайные величины X и Y слабо зависят друг от друга (коррелируют между собой), при этом наблюдается обратная зависимость.

Построение регрессионных моделей

а) Линейная модель.

Таблица 2

Вычисление коэффициентов модели:

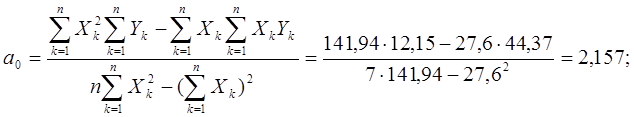
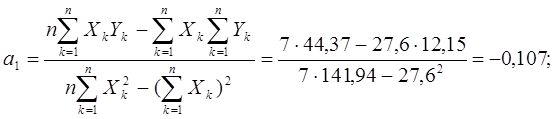
Уравнение регрессии имеет вид:

б) Квадратичная модель.

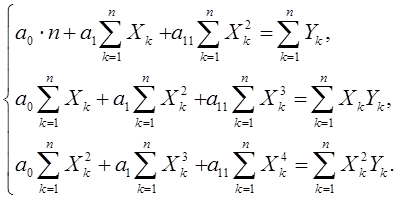
Для вычисления коэффициентов а₀, а₁, а₁₁ модели построим вспомогательную табл. 3.

Таблица 3

Исходные данные			Дополнительные столбцы
1	0,5	3,1	0,25	0,13	0,06	1,55	0,78
2	1,8	1,6	3,24	5,83	10,50	2,88	5,18
3	3,0	1,4	9,00	27,00	81	4,20	12,60
4	4,0	1,1	16,00	64,00	256,00	4,40	17,60
5	5,2	1,25	27,04	140,61	731,16	6,50	33,80
6	6,0	1,3	36,00	216,00	1 296,00	7,80	46,80
7	7,1	2,4	50,41	357,91	2 541,17	17,04	120,98
Суммы	27,6	12,15	141,94	811,48	4 915,89	44,37	237,74

Система уравнений принимает вид:

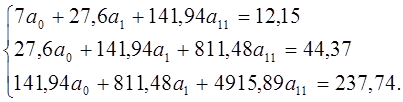
Решение СЛАУ методом Крамера:

         

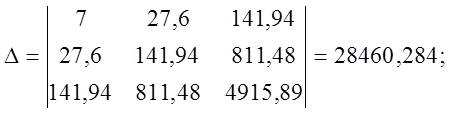
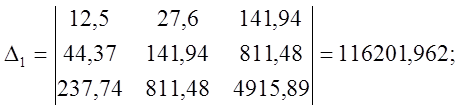
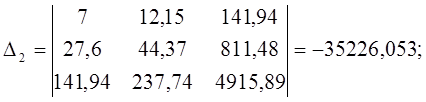
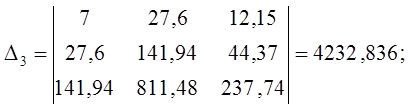
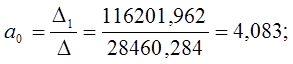
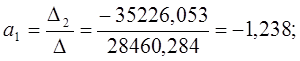
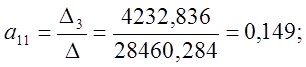
Статистическая модель принимает вид:

в) Степенная модель.

Вводим новые переменные:

Отсюда:

Обозначим:

 Тогда:

Получили линейную модель регрессионную модель:

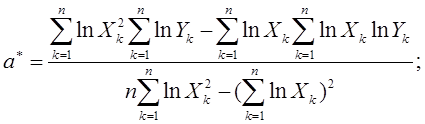
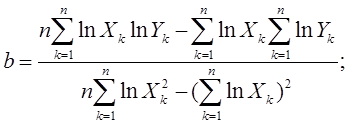
Таблица 4

Исходные данные			Дополнительные столбцы
1	-0,693	1,131	0,480	-0,784
2	0,588	0,470	0,345	0,276
3	1,099	0,336	1,207	0,370
4	1,386	0,095	1,922	0,132
5	1,649	0,223	2,718	0,368
6	1,792	0,262	3,210	0,470
7	1,960	0,875	3,842	1,716
Суммы	7,780	3,394	13,725	2,548

.

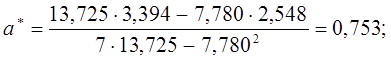
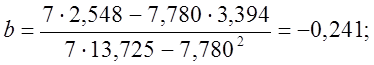
Графики моделей

Графики построены в программе Excel.