Расчет корреляционной связи между случайными величинами X и Y. Выбор лучшей модели по критерию Уилкса, страница 2

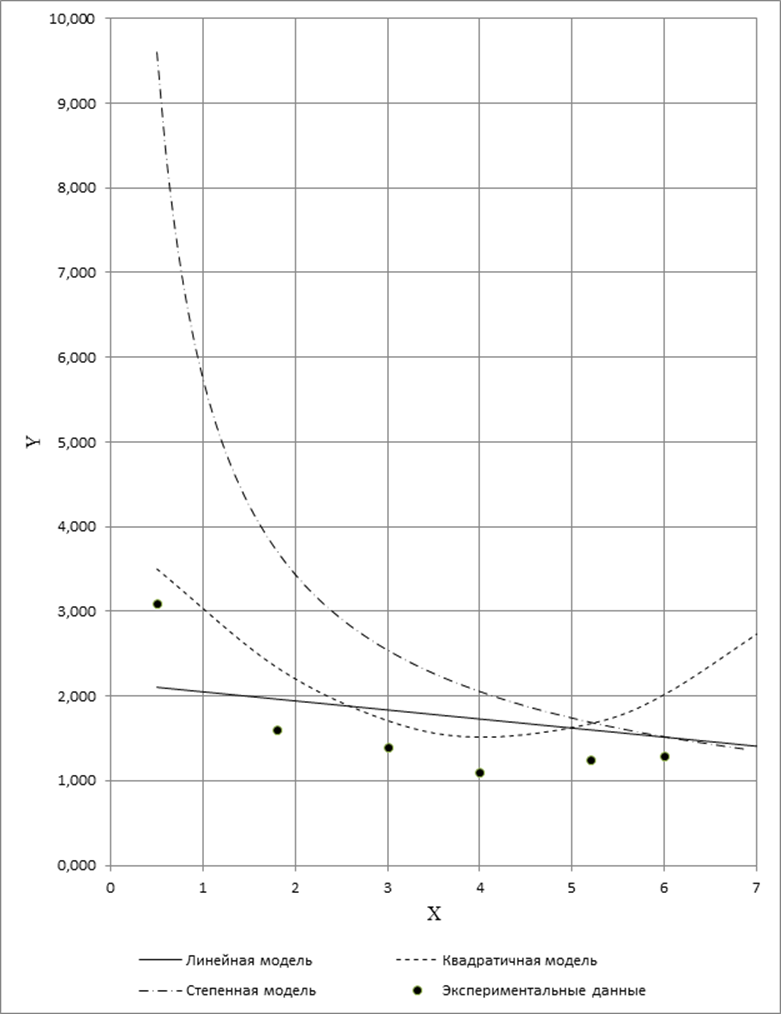
Рис. 1. Графики моделей

Выбор лучшей модели

;

.

Таблица 5

№	X	Y	η1i	η2i	η3i
1	0,5	3,1	2,104	3,501	2,509
2	1,8	1,6	1,964	2,337	1,843
3	3,0	1,4	1,836	1,710	1,629
4	4,0	1,1	1,729	1,515	1,520
5	5,2	1,25	1,601	1,674	1,427
6	6,0	1,3	1,515	2,019	1,379
7	7,1	2,4	1,397	2,804	1,324

Выбор лучшей модели по среднеквадратичной ошибке аппроксимации

Среднеквадратичная ошибка аппроксимации функции отклика S_rL1:

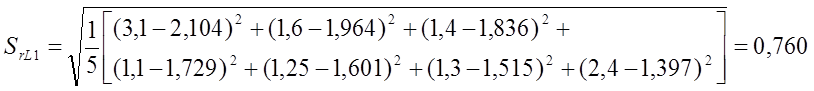
Среднеквадратичная ошибка аппроксимации функции отклика S_rL2:

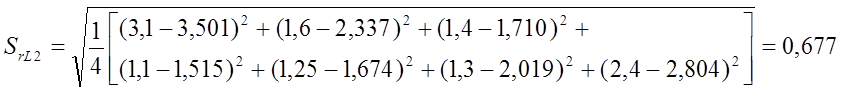
Среднеквадратичная ошибка аппроксимации функции отклика S_rL3:

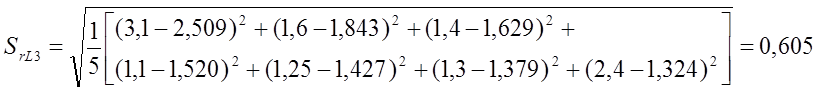
Статистическая модель предпочтительна, если ее среднеквадратичная ошибка аппроксимации имеет наименьшую величину по сравнению с другими рассматриваемыми моделями. В рассматриваемом случаеследовательно, наилучшей моделью с позиции выбора лучшей модели по среднеквадратичной ошибке аппроксимации является степенная модель η₃.

Выбор лучшей модели по критерию Уилкса

Линейная комбинация моделей:

Функционал ошибок:

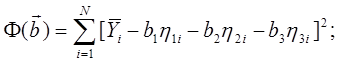
                Вычислим частные производные:

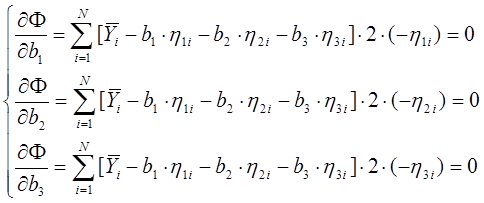
Раскрываем скобки и получаем систему уравнений:

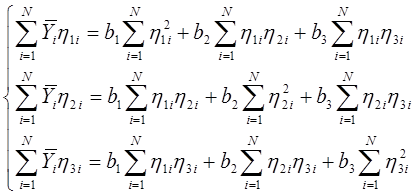
Таблица 6

     

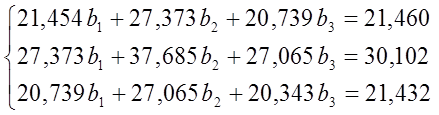
Решение СЛАУ методом Крамера:

         

        

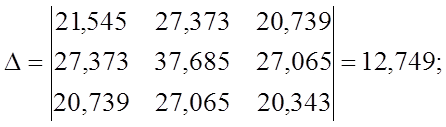
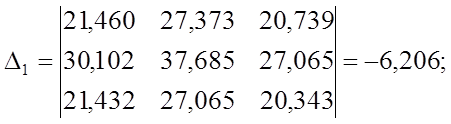
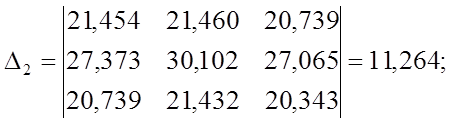
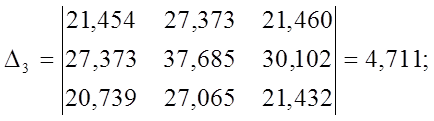
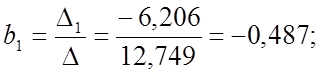
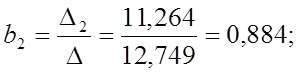
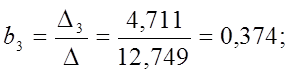
Чем больше величина коэффициента b_Q, тем лучше работает модель. Так как то квадратичная модель η₂ является наилучшей с точки зрения критерия Уилкса.

Выбор лучшей модели по комплексной функции качества

Комплексная функция качества

Линейная модель

Среднее значение отклика по всем точкам плана:

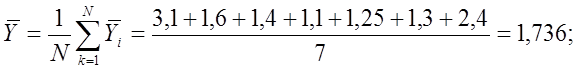
  – выборочное среднее отклика в i-й точке.

Относительная среднеквадратичная ошибка:

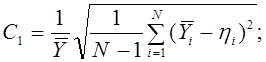
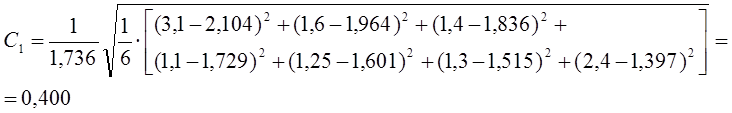
Относительная максимальная ошибка:

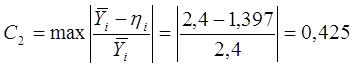
Коэффициент, характеризующий громоздкость модели:

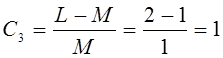
L – количество коэффициентов a_i в модели,

M – количество независимых переменных x_m.     

Коэффициент насыщенности модели:

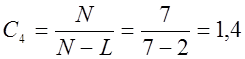
Коэффициент, характеризующий монотонность модели:

C₅ = 1 – для модели полиномного типа.

Коэффициент, характеризующий устойчивость модели к ошибке воспроизведения функции отклика:

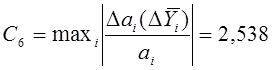
 – вариация отклика, взятая в пределах погрешности воспроизведения

Коэффициент, характеризующий устойчивость коэффициентов a_l к изменению независимых переменных:

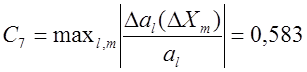
ΔX_m – вариация m–й независимой переменной, определяемая условно

ΔX_m = 10% |X_m|.

Квадратичная модель

Среднее значение отклика по всем точкам плана:

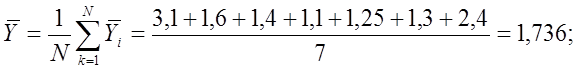
Относительная среднеквадратичная ошибка:

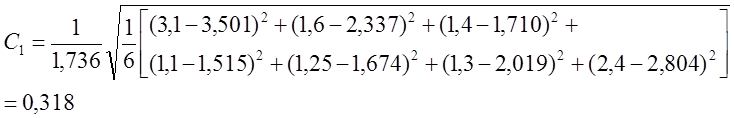
Относительная максимальная ошибка:

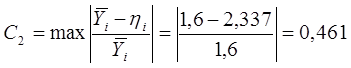
Коэффициент, характеризующий громоздкость модели:

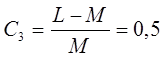
Коэффициент насыщенности модели:

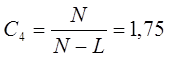
Коэффициент, характеризующий монотонность модели:

C₅ = 0,5 – для модели степенного типа.

Коэффициент, характеризующий устойчивость модели к ошибке воспроизведения функции отклика:

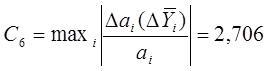
Коэффициент, характеризующий устойчивость коэффициентов a_l к изменению независимых переменных:

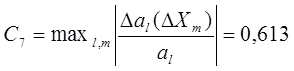
Степенная модель

Среднее значение отклика по всем точкам плана:

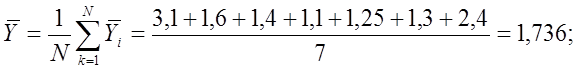
Относительная среднеквадратичная ошибка:

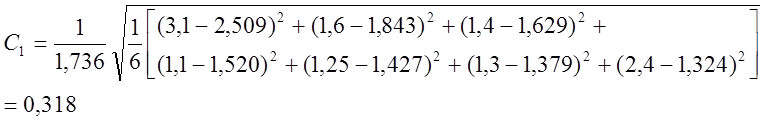
Относительная максимальная ошибка:

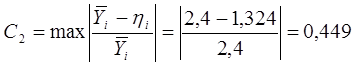
Коэффициент, характеризующий громоздкость модели:

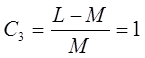
Коэффициент насыщенности модели:

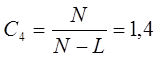
Коэффициент, характеризующий монотонность модели:

C₅ = 0,5 – для модели степенного типа.

Коэффициент, характеризующий устойчивость модели к ошибке воспроизведения функции отклика:

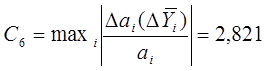
Коэффициент, характеризующий устойчивость коэффициентов a_l к изменению независимых переменных:

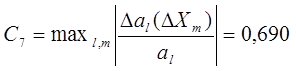
Лучшей считается модель, у которой величина функции качества С наименьшая, следовательно, по критерию комплексной функции качества лучшей является квадратичная модель.

Вывод

На первом этапе выполнения данного расчетного задания был выполнен корреляционный анализ, который показал, что случайные величины слабо коррелируют между собой, при этом наблюдается обратная зависимость. Далее были построены линейная, квадратичная и степенная модели, а также сформированы их графики. Затем был выполнен выбор наилучшей модели. Для этого использовались критерии: по среднеквадратичной ошибке аппроксимации, критерий Уилкса и критерий комплексной функции качества. Метод по среднеквадратичной ошибке аппроксимации указал на степенную модель. Критерий Уилкса указал на квадратичную модель. Критерий комплексной функции качества указал на квадратичную модель. На основании этих трёх критериев, в качестве лучшей принимаем квадратичную модель.