Разработка шестизвенного рычажного исполнительного механизма щековой дробилки

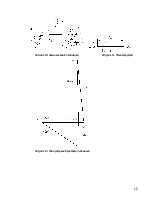
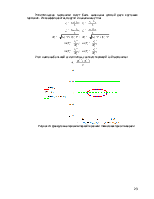
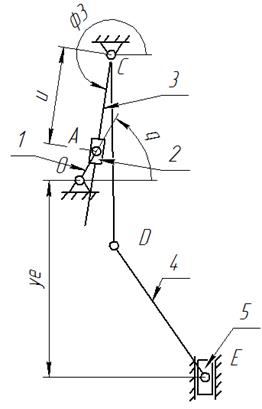
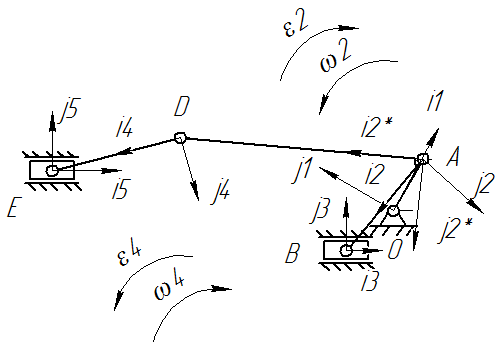
Звенья механизма: 1 – кривошип; 2 – камень; 3 – коромысло; 5 – ползун, 4 – шатун.

  (один вход О-А ).

Число подвижных звеньев механизма

количество кинематических пар совпадает с числом подвижностей пар

, т.е. два независимых контура: 0-1-2-3-0 и 0-3-4-5-0.

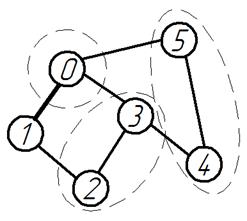
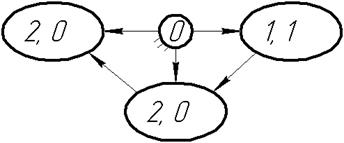
Рисунок 4. Схема                                            Рисунок 5. Граф механизма с подграфами

  (одна степень подвижности).

, т.е. рассматривается нормальный механизм.

В плоскости движения нет избыточных связей и лишних подвижностей.

Разделение графа механизма на подграфы, соответствующие структурным группам.

Для открытой цепи 0-1 выполняется условие: , т.е. . Для замкнутых цепей 1-2-3-0 и 0-5-4-3 выполняется условие: , т.е. имеется три тонких ребра. Механизм образован следующим образом: к стойке присоединяется однозвенная одноподвижная группа (звено 1) и две двухзвенные группы Ассура – ВПВ (звенья 2 и 3) и ВВП (звенья 4 и 5).

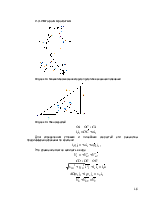
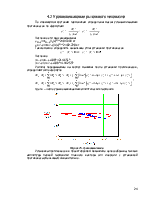
Рисунок 6. Структурный граф механизма

2.2 Геометрический и кинематический анализ (аналитический метод)

Размыкая кинематическую цепь в шарнирах А и C, приведем замкнутую цепь к открытой цепи (ветви: ОА, СА, CDE, BE).

На структурной схеме и графе механизма обозначим входную координату  и четыре групповые координаты:    Их число совпадает с числом разомкнутых связей:

Уравнения геометрического анализа.

Кривошип:

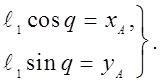
Группа ВПВ (2-3):

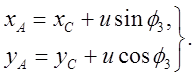
Группа ВВП (4-5):

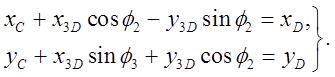
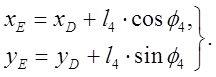
Решение групповых уравнений

Уравнения группы ВПВ, возведенные в квадрат и сложенные, дают выражение для относительной координаты. Замечено, что для такой структурной группы существует только один способ сборки.

Определение угла из уравнений группы ВПВ (2-3)

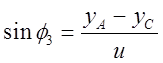
Из уравнений группы ВВП (4-5) получено:

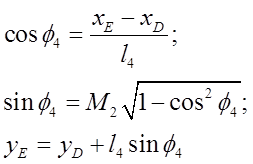
Здесь коэффициент сборки М₂=±1 перед радикалом указывает на два решения тригонометрических уравнений. Этим решениям соответствуют два варианта сборки звеньев 5 и 4 группы ВВП.

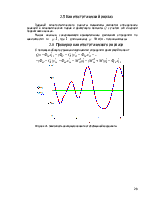
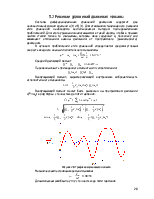
Исследование функций положения

Определение аналогов скоростей и ускорений выполнено путем двойного дифференцирования по обобщенной координате уравнений геометрического анализа. Для группы ВПВ (2-3), получено:

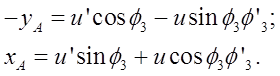
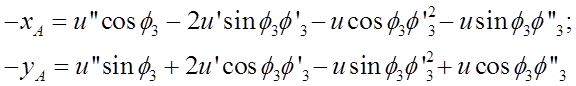
Отсюда по правилу Крамера

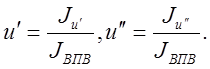
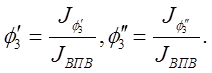
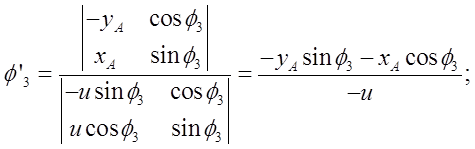
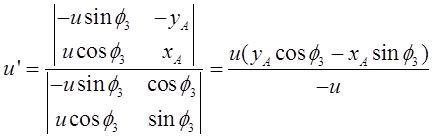
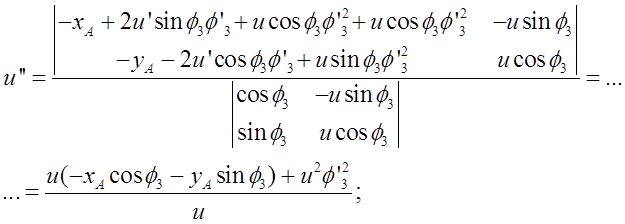
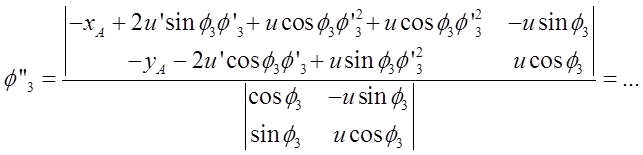
Определитель полученных систем уравнений совпадает с якобианом исходной системы уравнений группы ВВП и выражается формулой:

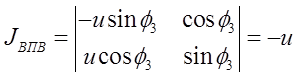
Из уравнений группы ВВП (4-5) дифференцированием получено:

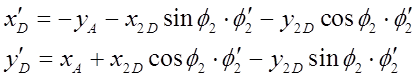
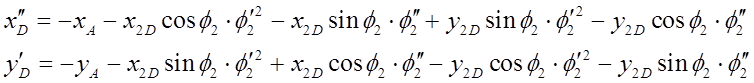
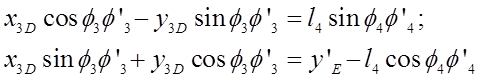
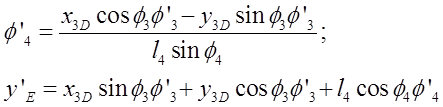
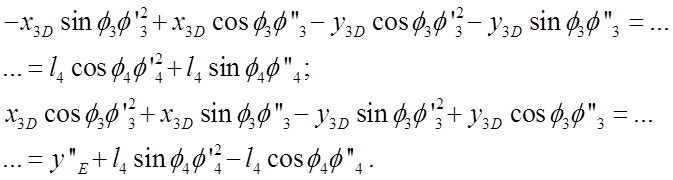
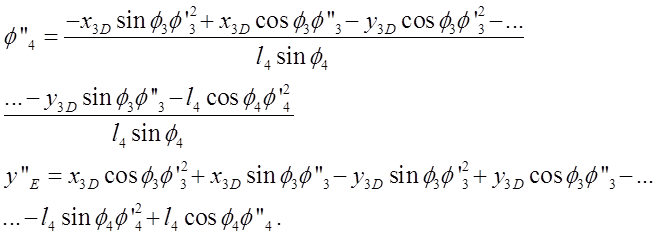
Якобиан системы уравнений группы ВВП:

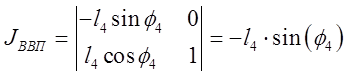
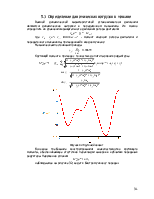
Группа ВПВ (2-3)  попадает  в особое положение при:

, т.е. камень 2 совпадает с точкой стойки С.

Особое положение группы ВВП (4-5) имеет место при выполнении условия: , т. е. когда

По значениям хода выходного звена H=60 град и коэффициента производительности Kv=1.4 были подобраны следующие постоянные геометрические параметры кинематической схемы механизма:

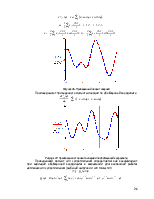
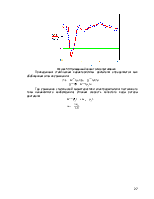
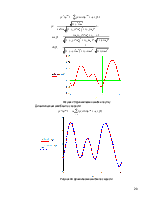
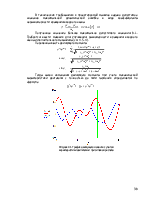
Графическое изображение функций положения и их производных – см. приложение.

Таблица 1. Сравнение двух прототипов

Здесь К1 – критерий качества передачи движения, характеризующий соотношение между внешними усилиями на входе и выходе. К2 – критерий качества передачи движения, характеризующий относительный уровень внутренних сил (реакций). Kv – коэффициент изменения средней скорости выходного звена (коэффициент производительности). Ход – угол между крайними положениями выходного звена – шатуна.

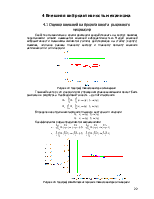
После проведения геометрического и кинематического анализа двух прототипов, сравнения критериев качества механизма, приведенных в таблице 1, сделан вывод, что первый прототип более выгоден, так как  коэффициенты К1 и К2 меньше, а габаритные размеры отличаются незначительно. Меньшие усилия ведут к более легким и дешевым шарнирам, соединениям. Графический метод кинематического анализа (построение планов скоростей и ускорений) производится для обоих прототипов.

2.3 Кинематический анализ (графический метод)

2.3.1 Первый прототип

Целью кинематического анализа является определение скоростей и ускорений отдельных точек и звеньев рычажного механизма по известному закону входного звена.

Определение скоростей и ускорения звеньев механизма и его шарнирных точек при помощи планов скоростей и ускорений.

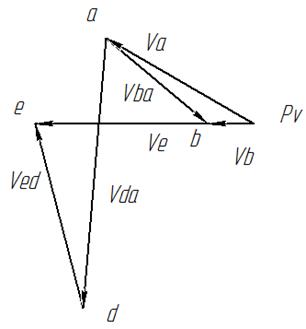
Для этого выполнена кинематическая схема механизма в расчетном