Проектирование узла привода одноступенчатого редуктора

1.  Схема и принцип действия привода

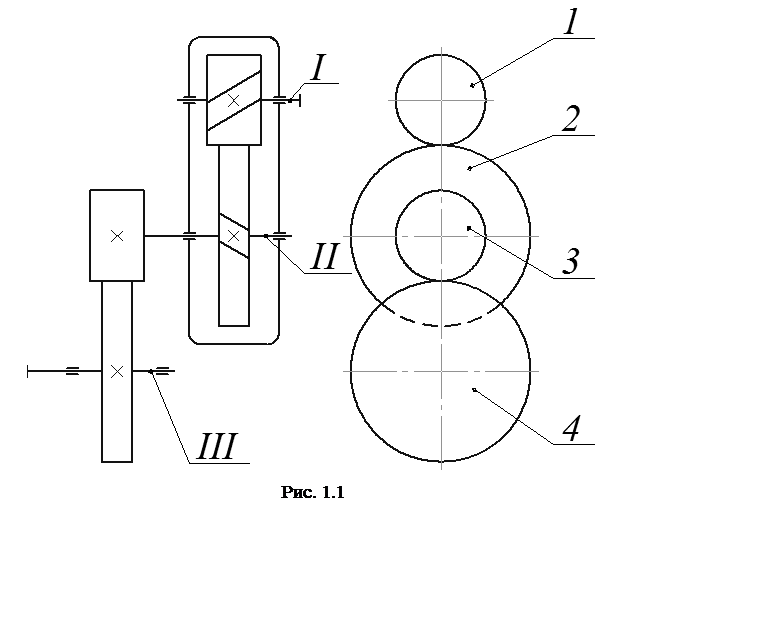
Вращение с вала электродвигателя через муфту передается на вал I одноступенчатого редуктора. Вращение с вала I на вал II передается при помощи косозубой передачи 1–2. Вращение с вала II на III передается с помощью прямозубой передачи 3–4. Узел привода, который необходимо спроектировать состоит из вала II и его опорных частей на подшипниках качения (рис. 1.1).

2.  Энерго-кинематический расчет

2.1.  Определение КПД передач и привода

КПД передач 1–2 и 2–3 вычисляются по формулам

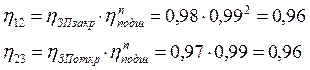                                                              (2.1)

где – КПД закрытой зубчатой передачи; – КПД открытой зубчатой передачи; – КПД пары подшипников; n – число пар подшипников.

Общее КПД привода вычисляется по формуле

                                                                    (2.2)

2.2.  Определение передаточных чисел

Составим систему уравнений

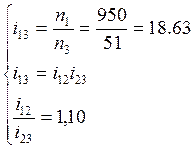                                                                                (2.3)

Решая данную систему уравнений, и округляя значения, получаем

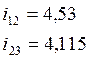                                                                                                  (2.4)

2.3.  Определение мощностей на валах привода

Мощность на валу III вычисляется по формуле

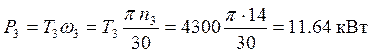                                                   (2.5)

Мощность на валу II вычисляется по формуле

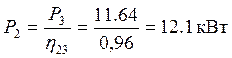                                                                          (2.7)

Мощность на валу I определяется по формуле

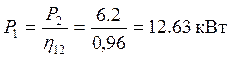                                                                          (2.8)

2.4.  Определение частот вращения валов

Частота вращения вала II определяется по формуле

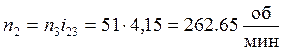                                                                  (2.9)

2.5.  Определение крутящих моментов на валах

Крутящий момент на валу II определяется по формуле

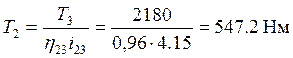                                                              (2.10)

Крутящий момент на валу I определяется по формуле

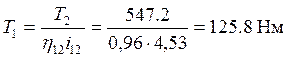                                                               (2.11)

2.6.  Таблица результатов энерго-кинематического расчета

3.  Расчет зубчатой передачи

3.1.  Проектировочный расчет

Так как в задании нет особых требований в отношении габаритов передачи, выбираем материалы со средними механическими характеристиками: для шестерни Сталь 45, термическая обработка – улучшение, твердость, в соответствии с заданием, HCR₁ = 46; для колеса – Сталь 45, термическая обработка – улучшение, но твердость на 20 единиц ниже – HCR₂ = 45.

Предел контактной выносливости при базовом числе циклом [1, с.34]

                                                                                 (3.1)

Эквивалентное число циклов для шестерни

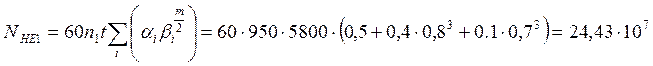    (3.2)

Эквивалентное число циклов для колеса

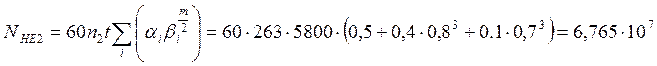                                                                         (3.3)

Коэффициент долговечности K_HL1 равен 101, т.к. N_E1>N_H0.

Коэффициент долговечности K_HL2 вычисляется по формуле

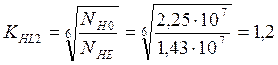                                                                  (3.4)

Коэффициент безопасности  примем равным 1,2.

Допускаемые контактные напряжения для шестерни [1, с.33]

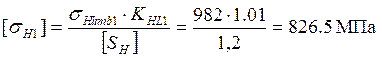                                                  (3.5)

Допускаемые контактные напряжения для колеса

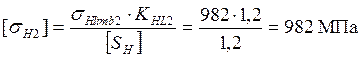                                                    (3.6)

Для косозубых колес расчетное допускаемое контактное напряжение равно:

                                    (3.7)

Учитывая симметричное расположение колес относительно опор, примем коэффициент K_Hb = 1,1 [1, с. 32].

3.2.  Расчет геометрических параметров зубчатых колес

3.2.1.  Определение межосевого расстояния

Принимаем для косозубых колес коэффициент ширины венца по межосевому расстоянию 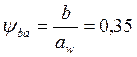 [1, с. 36].

Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев

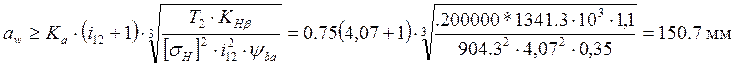                                                                (3.8)

где коэффициент K_a для косозубых колес равен 0.75 [1, с. 32].

Принимаем межосевое расстояние равным 150 мм

3.2.2.  Определение модуля

Нормальный модуль выбираем по следующей рекомендации:

                                                      (3.9)

принимаем по ГОСТ 9563-60 m = 2.5 мм

3.2.3.  Определение угла наклона зубьев

Примем предварительно угол наклона зубьев b = 20° и определим числа зубьев шестерни

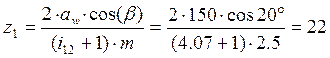                                                        (3.10)

Примем число зубьев шестерни равным 22

Число зубьев колеса

                                                                            (3.11)

Примем число зубьев колеса равным 90

Уточняем передаточное число i₁₂

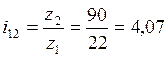                                                                                   (3.12)

Уточненное значение угла наклона зубьев

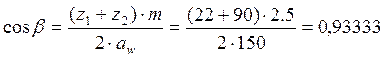                                               (3.13)

3.2.4.  Определение основных размеров шестерни и колеса

Делительные диаметры

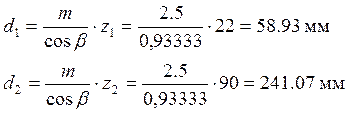                                                     (3.14)

Проверка правильности по межосевому расстоянию

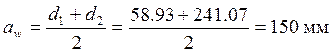                                                        (3.15)

Диаметры вершин зубьев

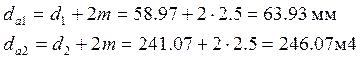                                                  (3.16)

Диаметры впадин зубьев

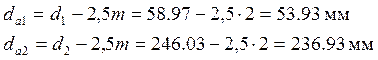                                                (3.17)

Ширина колеса

                                                                (3.18)

Ширина шестерни

                                                                    (3.19)

Коэффициент ширины шестерни по диаметру

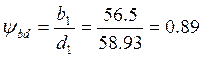                                                                             (3.20)

3.3.  Проверочный расчет на контактную выносливость

Окружная скорость колес и степень точности передачи

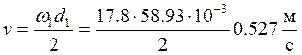                                                            (3.21)

При такой скорости выберем 8-ю степень точности. При этом , , . Коэффициент нагрузки

                                                  (3.22)

Коэффициент торцевого перекрытия

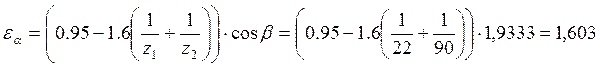                                                                                   (3.23)

Условие контактной выносливости

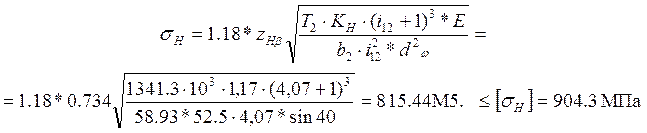                                                                               (3.24)

Из выполнения данного неравенства следует, что работоспособность по критерию контактной выносливости обеспечена.

3.4.  Проверочный расчет на изгибную прочность

Окружная сила, действующая в зацеплении

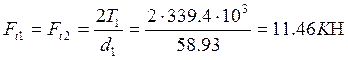                                                     (3.25)

Условие прочности зубьев на выносливость по напряжениям изгиба:

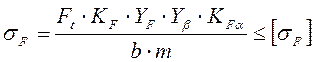                                                          (3.26)

Здесь коэффициент нагрузки

                                                                                       (3.27)

При , твердости HB£350 и симметричном расположении зубчатых колес относительно опор ,

Таким образом, по формуле (3.27), коэффициент нагрузки

Y_F – коэффициент, учитывающий форму зуба и зависящий от эквивалентного числа зубьев:

у шестерни ;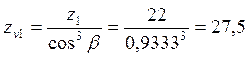

у колеса .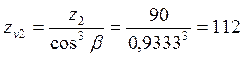

Тогда  и .

Для определения допускаемого напряжения используем формулу

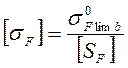                                                                                          (3.28)

Для стали 45 улучшенной при твердости HB£350

Для шестерни МПа; для колеса  540МПа.

Коэффициент безопасности

                                                                                  (3.29)

Коэффициент, выражающий степень ответственности  [1, с. 45], а коэффициент, учитывающий способ получения  (для поковок и штамповок) [1, с. 44].

Следовательно, по формуле (3.29):

По формуле (3.28) допускаемые напряжения:

для шестерни ;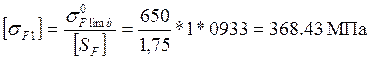

для колеса .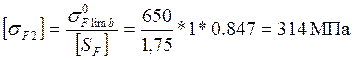

Дальнейший расчет проводим для зубьев того колеса, для которого найденное отношение меньше.

Определяем коэффициент Y_b

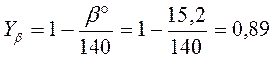                                                                 (3.30)

При учебном проектировании [1, с.47]

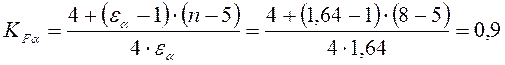                           (3.31)

где  –коэффициент торцового перекрытия; n - степень точности зубчатых колес.

Проверяем прочность зуба колеса по формуле (3.25)

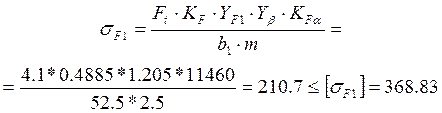                                      (3.32)

Из выполнения данного неравенства следует, что работоспособность по критерию изгибной выносливости обеспечена.

4.  Проектировочный расчет вала редуктора

Предварительный расчет проведем на кручение по пониженным допускаемым напряжениям.

Диаметр выходного конца вала при допускаемом напряжении

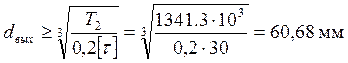                                                       (4.1)

Примем, с запасом, большее значение из стандартного ряда . Диаметр вала под подшипниками принимаем , под зубчатым колесом .

Диаметры остальных участков вала назначаются из конструктивных соображений при компоновке редуктора.

5.  Определение полных реакций на валу

5.1.  Схема сил, действующих в зацеплении

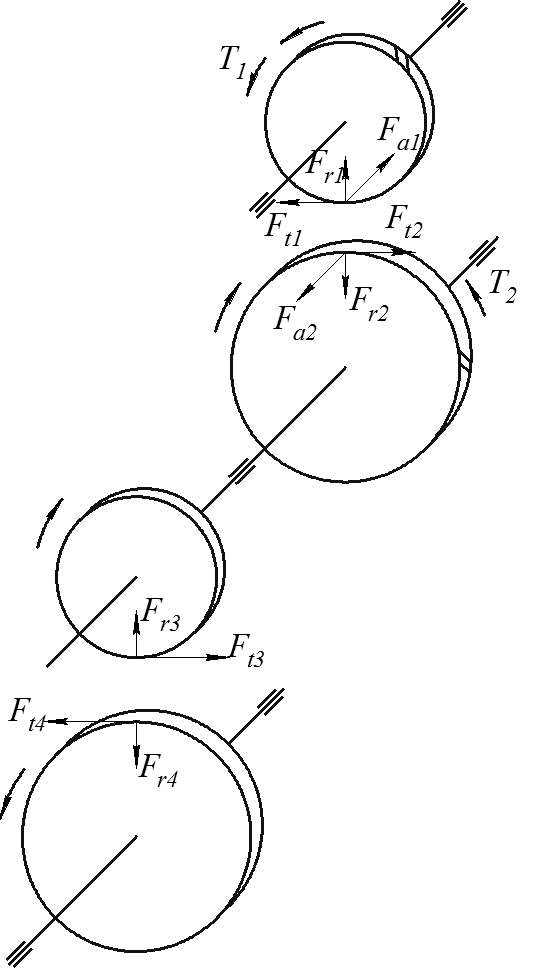
Рис. 5.1

5.2.  Определение сил, действующих в зацеплении второго колеса

Окружная сила из формулы (3.25)

                                                                                   (5.1)

Осевая сила

                                                        (5.2)

Радиальная сила

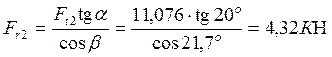                                                          (5.3)

5.3.  Определение сил, действующих в зацеплении третьего колеса

Окружная сила:

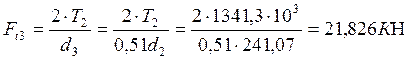                                            (5.4)

Радиальная сила

                                                          (5.5)

5.4.  Определение реакций на валу

5.4.1.  Определение реакций в горизонтальной плоскости

В горизонтальной плоскости расчетная схема вала выглядит, как показано на рис. 5.2. Размеры a и b находятся из чертежа. ,

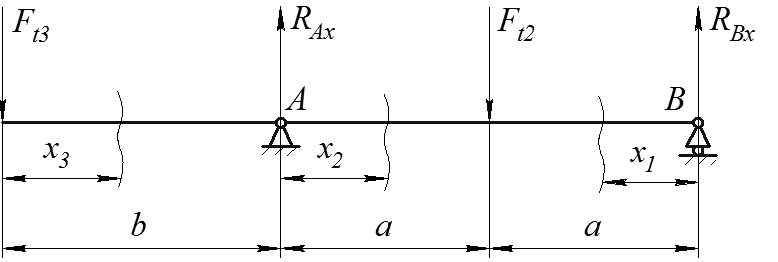
Рис. 5.2

Составим уравнения равновесия для горизонтальной плоскости.

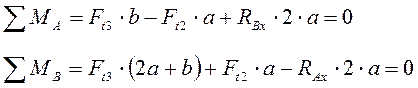                                            (5.6)

Отсюда

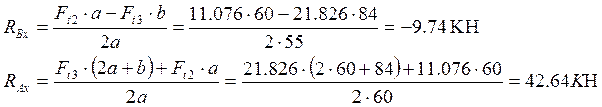
Проверка

5.4.2.  Определение реакций в вертикальной плоскости

В вертикальной плоскости расчетная схема вала выглядит, как показано на рис. 5.3

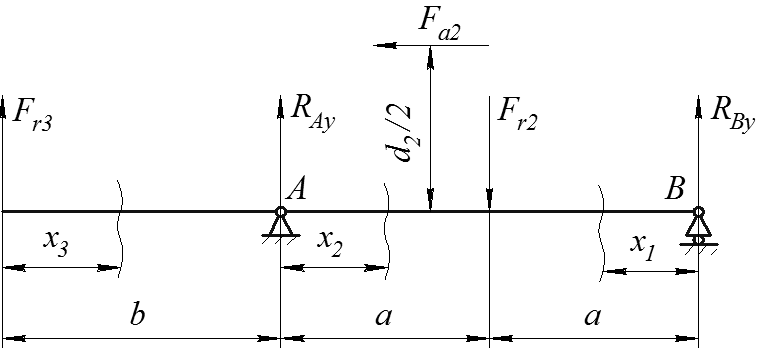
Рис. 5.3

Составим уравнения равновесия для вертикальной плоскости.

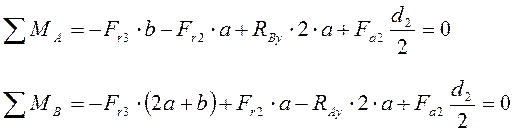                           (5.7)

Отсюда

Проверка

5.5.  Выражения моментов, необходимые при построении эпюр

5.5.1.  Выражения для моментов для горизонтальной плоскости

5.5.2.  Выражения для моментов для вертикальной плоскости

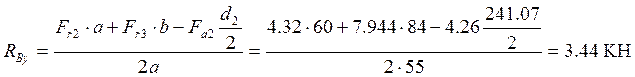
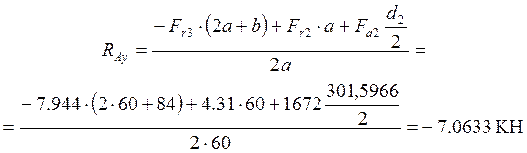
5.5.3.  Определение суммарного момента

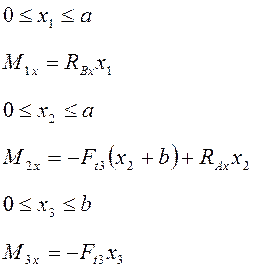
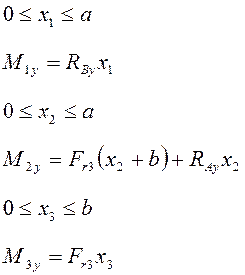
Суммарный момент определяется по формуле

                                                                                    (5.8)

5.6.  Эпюры моментов

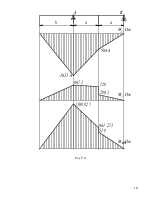
Эпюры приведены на рис. 5.4

Рис 5.4

6.  Расчет шпоночных соединений

6.1.  Расчет шпонки на концевом участке вала

6.1.1.  Проектировочный расчет на смятие

Сила, действующая на шпонку

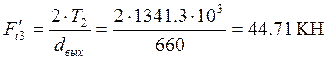                                                          (6.1)

Выбираем шпонку 18х11. Рабочая длина шпонки находится из условия смятия

                                                                                                                 (6.2)

Тогда полная длина

                                                                                                  (6.3)

Принимаем длину шпонки равную 51 мм

6.1.2.  Проверочный расчет на срез

Условие прочности имеет вид

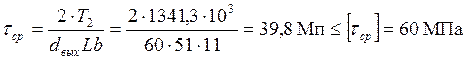                                   (6.4)

Из выполнения данного неравенства следует, что работоспособность