Проектирование узла привода (КПД привода равен 0,88; передаточное число привода - 18,6), страница 2

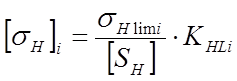
           где [S_H] - коэффициент надежности (примем его равным 1,2)

          Рассчитаем допускаемые напряжения для шестерни и колеса:

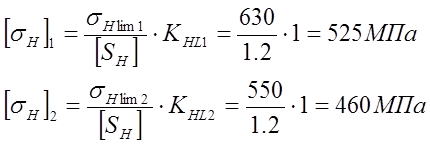
          Определим общее значение допускаемых напряжений:

3.       Определение размеров передачи

3.1     Определение межосевого расстояния

Межосевое расстояние по условию контактной выносливости вычисляется по следующей формуле:

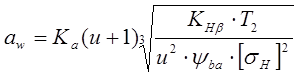 мм,

где  - коэффициент нагрузки, =1,15;  - коэффициент ширины венца, =0,3. Подставляя значения в формулу, получаем:

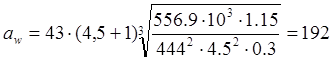 мм

Уточняя значение межосевого расстояния по ГОСТ получаем:

3.2     Определение модуля косозубой передачи

               Модуль передачи определяется по следующей формуле:

 мм,

          тогда подставив значение межосевого расстояния получаем:

 мм

          По ГОСТ 9563-60 выбираем  мм.

3.3     Определение числа зубьев шестерни и колеса и угла наклона

          Определяем количество зубьев шестерни по следующей формуле:

,

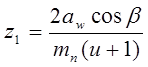          где  - угол наклона зуба, в первоначальном приближении равен 16°.

          Тогда количество зубьев колеса определяется как:

          Подставим значения в формулы и найдем количество зубьев колеса и шестерни:

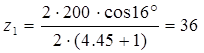
Количество зубьев колеса соответственно равно:

Уточняем угол наклона зуба:

3.4     Определение диаметров шестерни и колеса

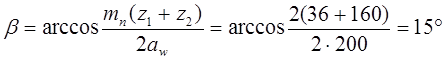
Вычисляем диаметры начальных окружностей шестерни и колеса

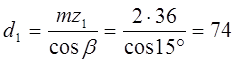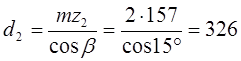 мм

 мм

Проверяем правильность проведённого расчёта по формуле

          3.5     Определение ширины венцов колеса и шестерни

 мм

 мм

          Коэффициент ширины шестерни по диаметру

3.6     Проверка расчета по контактным напряжениям

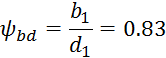
          Окружная скорость колеса:

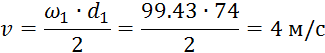
          Определяем коэффициент нагрузки для проверки контактных напряжений:

где =1.05 - коэффициент неравномерности распределения нагрузки по ширине венца при расчёте на контактную выносливость зубьев; =1 - коэффициент динамичности при расчёте на контактную выносливость зубьев, равен 1 при скорости менее 5 м/с, =1.09 – учитывает окружную скорость и степень точности.

Таким образом:

Проверка контактных напряжений производиться по следующей формуле:

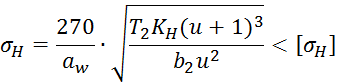
          Подставляя значения в формулу получаем:

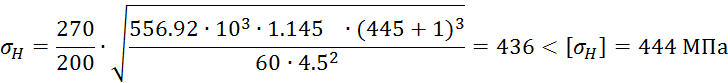
          Таким образом можно сделать вывод, что условие прочности по контактным напряжениям выполнено.

3.7     Проверка расчета по изгибным напряжениям

          Определим силы, действующие в зацеплении:

Окружная сила              

Радиальная сила            

Осевая сила                   

где  - угол зацепления, а   - угол наклона зубьев.

          Проверка зубьев на выносливость производиться по следующей формеле:

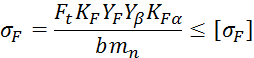
где, коэффициент нагрузки =1.13·1.25=1.41

Коэффициент, учитывающий форму зуба,  выбирается в зависимости от эквивалентных чисел зубьев:

, тогда  

Допускаемое напряжение:

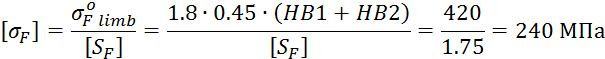
Коэффициент  учитывает повышение прочности косых зубьев по сравнению с прямыми:

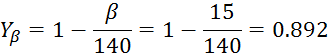
Коэффициент  учитывает распределение нагрузки между зубьями.

,

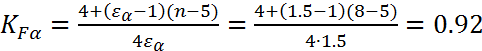где n- степень точности колес

Проверка ведется по зубьям колеса:

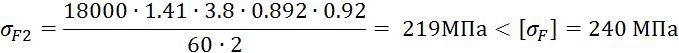
          Таким образом можно сделать вывод, что условие прочности по изгибным напряжениям выполнено.

Следовательно размеры передачи подсчитаны верно.

3.8     Вычисление диаметра впадин и вершин зубьев:

          Для колеса и шестерни диаметры впадин и диаметры вершин зубьев рассчитываются по следующим формулам:

3.9     Расчет третьего колеса передачи

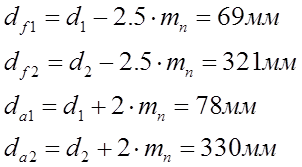
          Расчет производиться по следующим формулам:

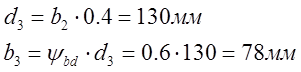
          Определим модуль третьего колеса:

          Определим количество зубьев колеса:

          Определим диаметры вершин и впадин третьего колеса:

4.       Определение реакций, сил и моментов в передаче

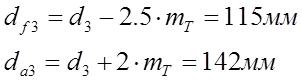
          На рис.2 приведена кинематико-расчетная схема механизма:

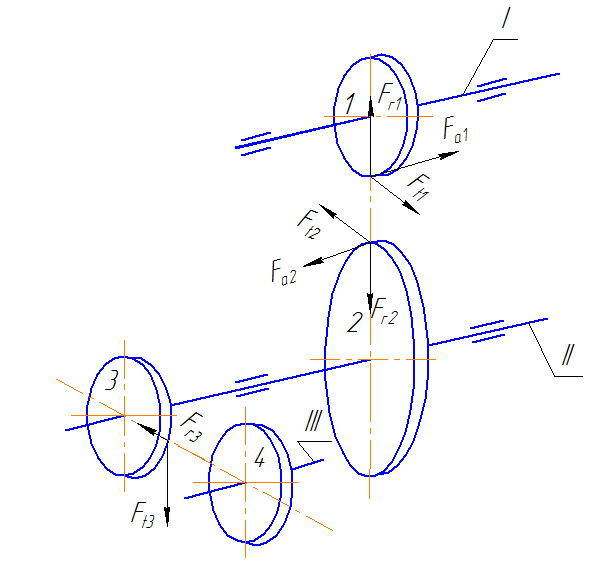
рис.2. Кинематико-расчетная схема механизма

          Определим силы, действующие в зацеплении

          Для колеса 2 (косозубое):

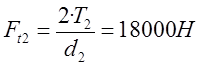
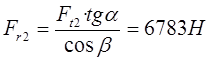
          Для колеса 3 (прямозубое):

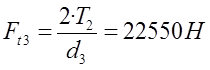
Где и - окружные силы для соответствующих колес, Н.

        и - радиальные силы для соответствующих колес, Н.

         - осевая сила на втором колесе, Н.

 4.1    Выбор расчетной схемы и определение расчетных нагрузок

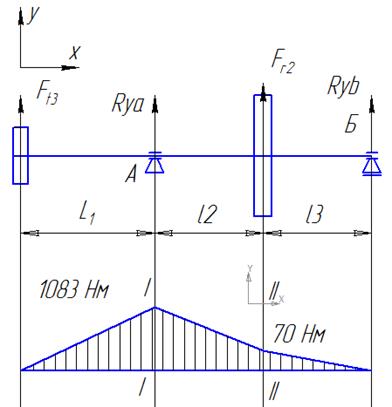
Представим расчетную схему вала в виде балки (рис.3.), расположенной на опорах А и Б в вертикальной (В) и горизонтальной (Г) плоскости.

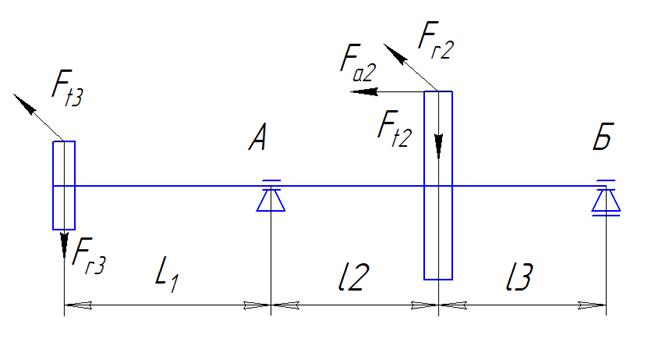
рис.3. Расчетная схема вала

Расстояния l1 l2 l3 определим с учетом параметра a, равного

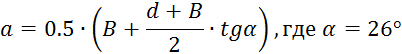
Подставим значения расстояний, получаем a=30мм., тогда l1=132 мм., l2 = l3 = 55 мм.

Определим реакции в опорах Ra и Rb :

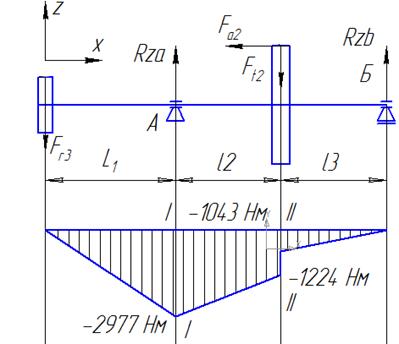
Составим уравнения равновесия и найдем реакции в опорах.

SM(A)=0=F_t3·l1-F_r2·l2+R_В·(l2+l3)+=0

SM(B)=0=F_r2·l3-R_A·(l2+l3)+F_t3·(l1+l2+l3)+=0

Из уравнений находим реакции:

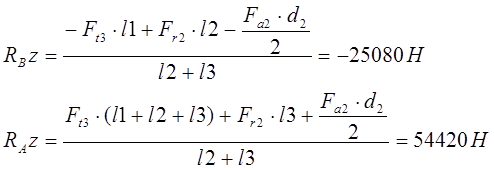
Проверим по условию SF_z=0, условие выполняется.

Составим уравнения равновесия и найдем реакции в опорах.

SM(A)=0=-F_t3·l1+F_t2·l2-R_Вy·(l2+l3)=0

SM(B)=0=-F_t2·l3+R_Ay·(l2+l3)-F_r3·(l1+l2+l3)=0

Из уравнений находим реакции:

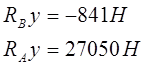
Проверим по условию SFy=0, условие выполняется.

        Анализируя эпюры изгибающих моментов, можно сделать вывод, что наиболее нагруженным сечением является сечение I-I.