Минимальная ширина венца цилиндрической передачи внешнего зацепления:
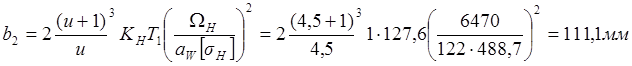
![]()
Расчетное напряжения на выносливость:
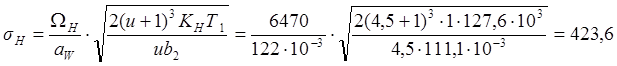 МПа
МПа
Проверка
контактных напряжений: ![]()
Условие контактной выносливости зубьев выполнено.
Условие статической контактной прочности
Задачей этого
пункта является, недопустимость обмятия профилей при кратковременных
перегрузках передачи. ![]()
Допускаемое
напряжение при расчёте на статическую прочность находят по формуле: ![]()
Расчётное
напряжение при расчёте на статическую прочность находят по формуле: ![]()
Проверка
контактных напряжений: ![]()
Условие статической контактной прочности зубьев выполнено.
Расчет цилиндрической косозубой передачи
на изгибную выносливость.
Задачей этого пункта является проверка зубьев шестерни и колеса на изгибную выносливость. Основной вид разрушения – усталостная поломка зуба.
Условие изгибной выносливости зубьев:
![]() ,где sF и [sF] – расчетное и
допустимое напряжения на изгиб.
,где sF и [sF] – расчетное и
допустимое напряжения на изгиб.
Найдем допускаемые контактные напряжения по формуле:
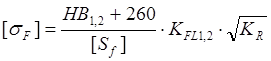 ,
где
,
где ![]() - предел контактной выносливости при
базовом числе циклов,
- предел контактной выносливости при
базовом числе циклов,
Sf – коэффициент безопасности =1,1,
![]() =1 –коэффициент учитывающий реверсивность
нагрузки.
=1 –коэффициент учитывающий реверсивность
нагрузки.
Коэффициент долговечности:
![]() ,
,
где ![]() - эквивалентное число цикло,
- эквивалентное число цикло,
где mf=6 показатель степени кривой выносливости для
зубьев с НВ![]() 350.
350.
Допускаемые контактные напряжения находятся отдельно для колеса и шестерни:
![]()
![]()
Посчитаем:
![]()
![]()
Для шестерни и колеса имеем:
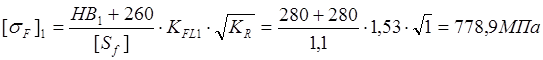
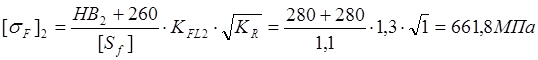
Расчетное напряжения изгибной выносливости:
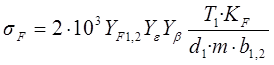 ,
,
где KF=1,3 – коэффициент нагрузки,
![]() - коэф., учит. торц. перекрытие,
- коэф., учит. торц. перекрытие,
![]() - коэффициент, учитывающий влияние наклона
зуба,
- коэффициент, учитывающий влияние наклона
зуба,
![]() - коэффициент прочности наружных зубьев,
- коэффициент прочности наружных зубьев,
![]() - диаметр начальной окружности шестерни,
- диаметр начальной окружности шестерни,
m– модуль цилиндрической передачи.
По условиям прочности найдём минимальные межосевые расстояния:
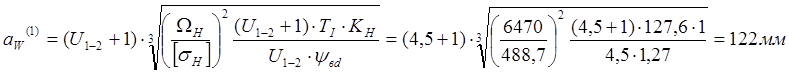
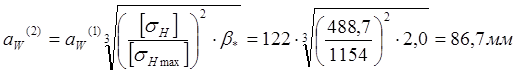
Рассчитаем минимальные числа зубьев, (β=20°):
![]()
![]()
По найденным числам зубьев вычисляем соответствующие им величины модулей, предварительно посчитав неизвестные коэффициенты:
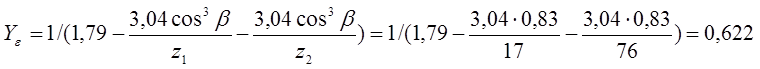
![]()
![]()
из условия изгибной выносливости:
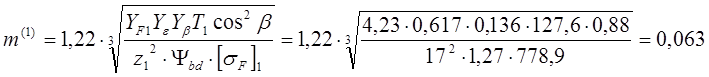
из условия стат. изломной прочности зубьев шестерни:
![]()
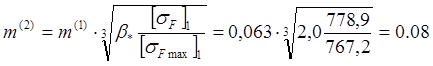
из условия изгибной выносливости:
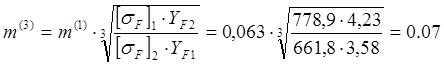
из условия стат. изломной прочности зубьев колеса:
![]()
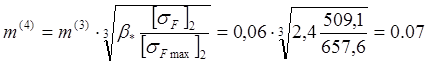
Примем за mmax=0,08 наибольшее из найденных знач. модулей m(1-4) он отвечает всем условиям почности и используется для расчёта минимального межосевого расстояния по усл. изломной прочности:
![]()
Принимаем за ![]() =
=![]() = 122 наибольшее из
трёх мин. межосевых расстояний.
= 122 наибольшее из
трёх мин. межосевых расстояний.
В качестве расчётного модуля mпринимаем наименьшее из стандартого ряда по ГОСТ (9563-60),но которое будет не менее величины кm=0,01aw=1,220
Примем m=2мм.
По рассчитанным модулю и мин. меж. расстоянию находим числа зубьев:
![]()
![]()
Уточнённое знач. угла наклона зуба:
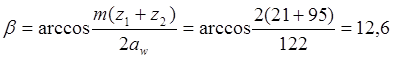 °
°
Тогда:
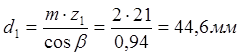 - делительный диаметр шестерни.
- делительный диаметр шестерни.
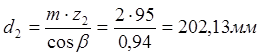 - делительный
диаметр колеса.
- делительный
диаметр колеса.
Проверка: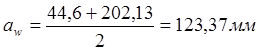
Условие изгибной выносливости: ![]()
Допускаемые контактные напряжения для колеса и шестерни:
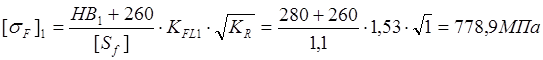
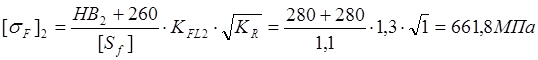
Расчётные контактные напряжения для колеса и шестерни:
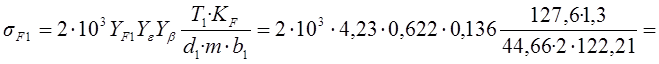 102,6МПа
102,6МПа
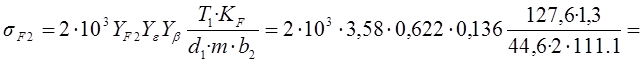 202,9МПа
202,9МПа
Проверка:
![]()
![]()
Условие изгибной выносливости зубьев выполнено.
Условие статической изломной прочности
Задачей этого
пункта является, предотвращения их статической поломки при перегрузках
передачи. ![]()
Допускаемое напряжение при расчёте на статическую прочность находят по формуле:
![]()
![]()
Расчётное напряжение при расчёте на статическую прочность находят по формуле:
![]()
![]()
Проверка:
![]()
![]()
Условие статической изломной прочности выполнено.
5. Проектировочный расчет ведомого вала.
По формуле приближенно оцениваем диаметры промежуточного вала вала под прямозубой шестерней: 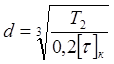
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.