Математическая обработка результатов эксперимента (исходная функция: y=c*xn)

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Санкт-Петербургский

государственный политехнический университет»

Институт металлургии, машиностроения и транспорта

Кафедра «Станкостроение »

Отчёт

по лабораторной работе № 1

“ Математическая обработка результатов эксперимента”

Студент гр. 43321/1                                            Дмитриев В.С.

.

                Преподаватель                                                     Адмакин М.А.

<<___>>_______________ 2013г.

Санкт-Петербург

2013 г.

1.  Задание

Исходные данные:

Таблица 1

X	15	20	25	30
Y	200	230	270	308

Исходная функция: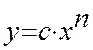

Прологарифмировав обе части выражения получим:

lg(y)=lg(c)+nlg(x)

Необходимо найти неизвестные параметр с и n.

2.  Обработка результатов

2.1.  Графический метод

Таблица 2

N	X	Y
1	15	200	1,18	2,30	191,51	4,25
2	20	230	1,30	2,36	232,89	1,26
3	25	270	1,40	2,43	271,05	0,39
4	30	308	1,48	2,49	306,82	0,38
Сумма						6,28

График в координатах  lgY-lgX  представлен в приложении.

Тангенс угла наклона аппроксимирующей прямой на графике есть  показатель степени в выражении . Согласно графику имеем:

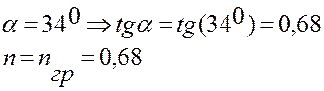
Определение коэффициента с в выражении :

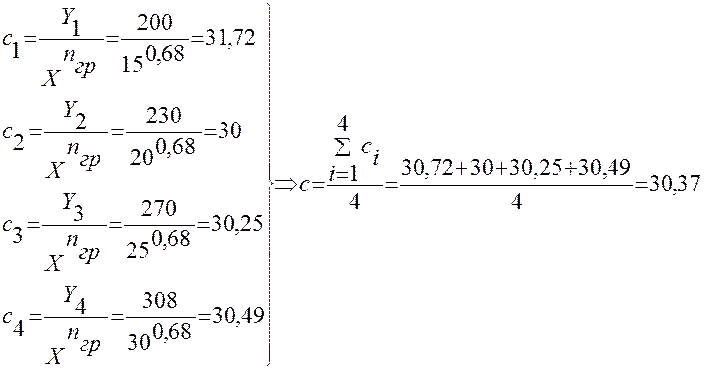
Расчет значений :

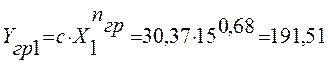
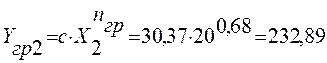
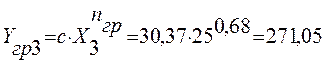
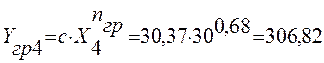
Расчет значений погрешности Δ:

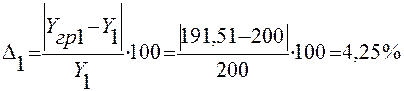
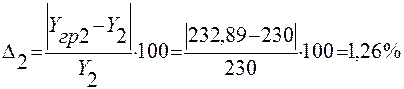
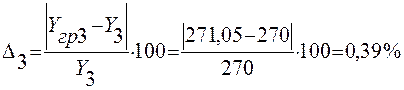
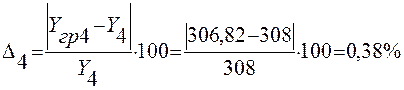
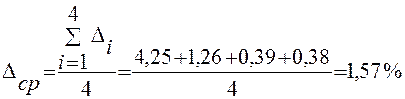
2.2.  Метод  средних

Таблица 3

N	X	Y
1	15	200	1,18	2,30	195,17	2,42
2	20	230	1,30	2,36	235,30	2,30
3	25	270	1,40	2,43	272,03	0,75
4	30	308	1,48	2,49	306,25	0,57
Сумма						6,04

Расчет показателя степени n:

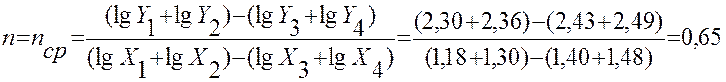
Определение коэффициента с в выражении :

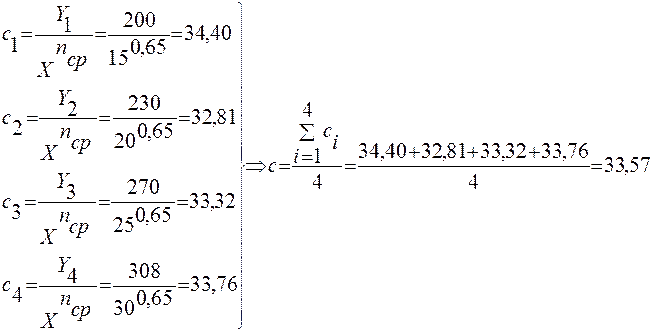
Расчет значений  :

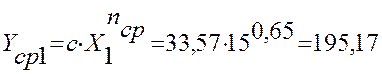
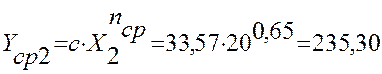
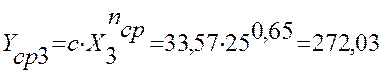
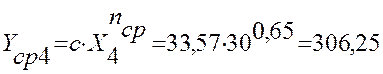
Расчет значений погрешности Δ:

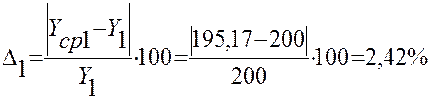
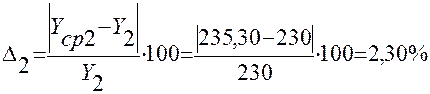
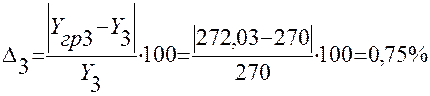
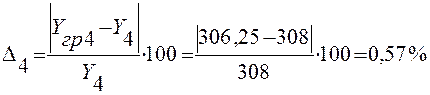
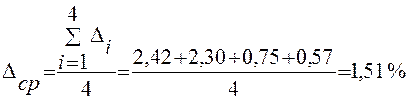
2.3.  Метод  наименьших квадратов

Таблица 4

N	X	Y			lgX2	lgX∙lgY
1	15	200	1,18	2,30	1,39	2,71	186,08	6,96
2	20	230	1,30	2,36	1,69	3,07	226,29	1,61
3	25	270	1,40	2,43	1,96	3,40	263,37	2,46
4	30	308	1,48	2,49	2,19	3,69	298,13	3,21
Сумма			5,36	9,58	7,23	12,87		14,24

Расчет показателя степени n:

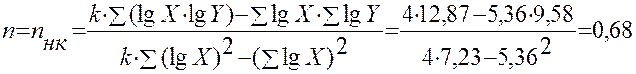
Определение коэффициента с в выражении :

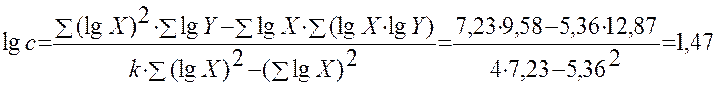
Расчет значений  :

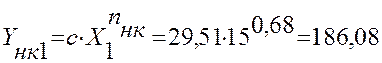
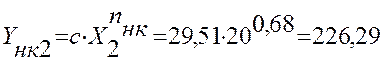
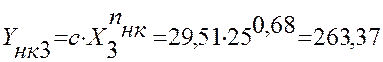
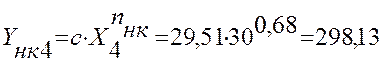
Расчет значений погрешности Δ:

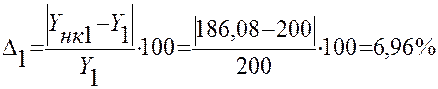
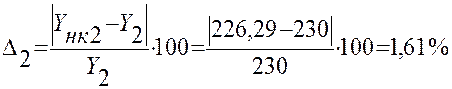
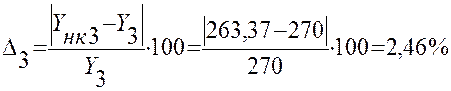
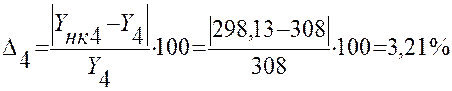
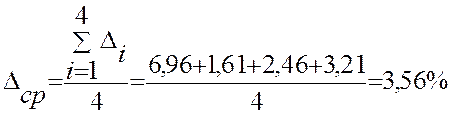
4.  Вывод

Обработав экспериментальные данные тремя методами получили следующие выражения зависимости  и соответствующие погрешности методов:

графический метод - , ;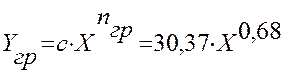

метод средних - , ;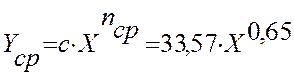

метод наименьших квадратов - , .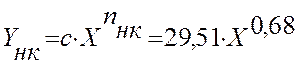

Все три метода позволяют определить коэффициент c и степень n достаточно точно, с погрешностью в пределах 5%. Следовательно можем использовать для обработки экспериментальных данных любым из этих методов.