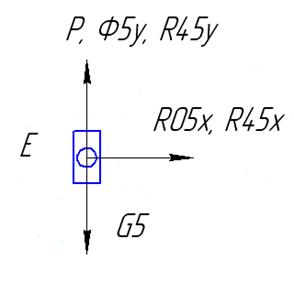
Машиностроение \ Теория машин и механизмов

Исследование механизмов с пятью подвижными звеньями, страница 3

Ползун 5

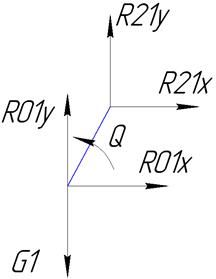Рис. 2.5

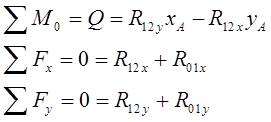Кривошип

Рис. 2.6

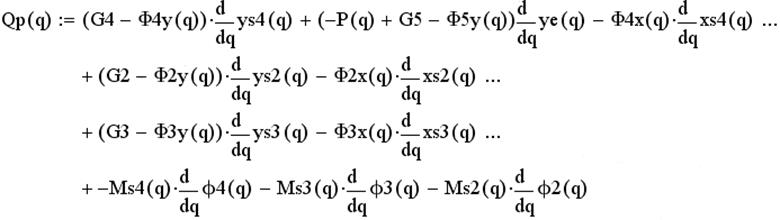2.5. Сравнение результатов, полученных различными методами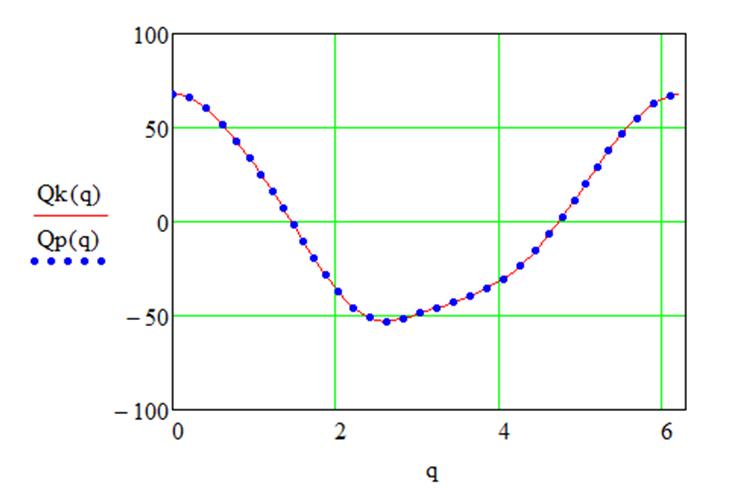

Рис. 2.7

Сравнение результатов расчета со стандартной программой

Параметр	Кинетостатический расчет	Стандартная программа
R05x	-262.041	-308.4454
R05y	0	0
R45x	262.041	308.4454
R45y	237.695	237.7517
R42x	245.46	339.1861
R42y	439.728	414.6965
R03x	247.806	313.2221
R03y	691.041	816.5352
R12x	-152.365	-157.7857
R12y	771.058	648.0956
R01x	-152.365	-162.17
R01y	807.834	682.3519
Q	55.795	49.2067

3. Механизм второй. Часть 1

3.1. Исходные данные

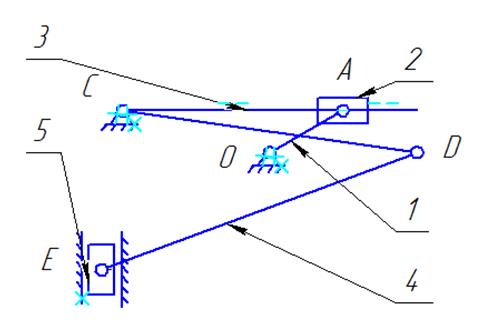
Рис. 3.1

3.1.

3.2. Структурный анализ

Звенья механизма 1 – кривошип; 2 –камень; 3 – кулиса; 4 – шатун; 5 – ползун (см. рис. 2.1.1.1).
(один вход О-А).
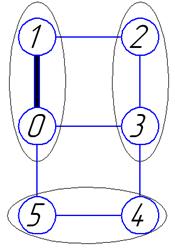
Граф механизма:

Рис. 3.2

Число подвижных звеньев механизма количество кинематических пар совпадает с числом подвижностей пар
(одна степень подвижности).
, т.е. рассматривается нормальный механизм.
В плоскости движения нет избыточных связей и лишних подвижностей.
Разделение графа механизма на подграфы, соответствующие структурным группам:
вход 0-1;
структурные группы: 2-3; 4-5
Структурный граф механизма:

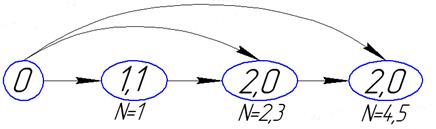
Рис. 3.3

Механизм образован следующим образом: к стойке присоединяется однозвенная одноподвижная группа (звено 1) и две двухзвенные группы Ассура – ВВП (звенья 2 и 3) и ВВП (звенья 4 и 5).

3.3. Геометрический анализ

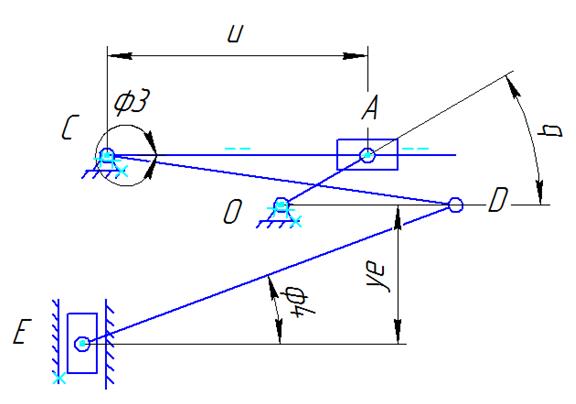
Рис. 3.4

Запишем уравнения геометрического анализа.

Группа ВПВ (2-3 звенья)

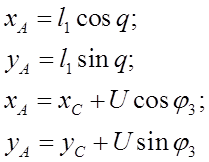
Неизвестные: U,.

Отсюда

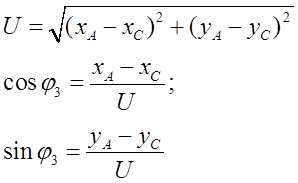
Группа ВВП(4-5 звенья)

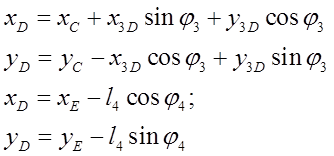
Неизвестные: ,

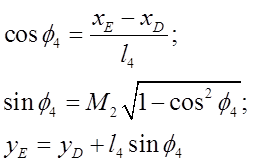
Продифференцируем полученные выражения для функций положения.

Группа ВПВ (2-3 звенья)

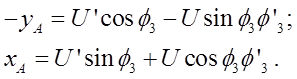
Неизвестные: , .
По правилу Крамера

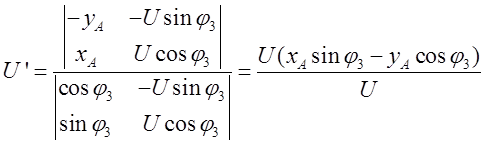
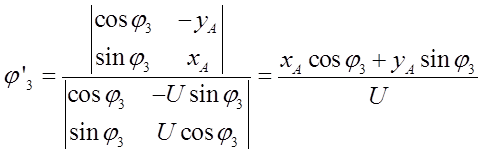
Таким образом, при механизм будет находится в особом положении.

Группа ВВП(4-5 звенья).

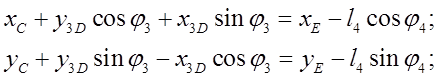
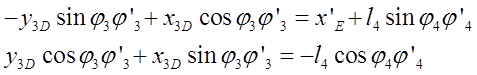
Неизвестные: ,

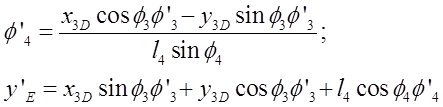
Механизм в особом положении пригде

Механизм в особом положении. Способы сборки

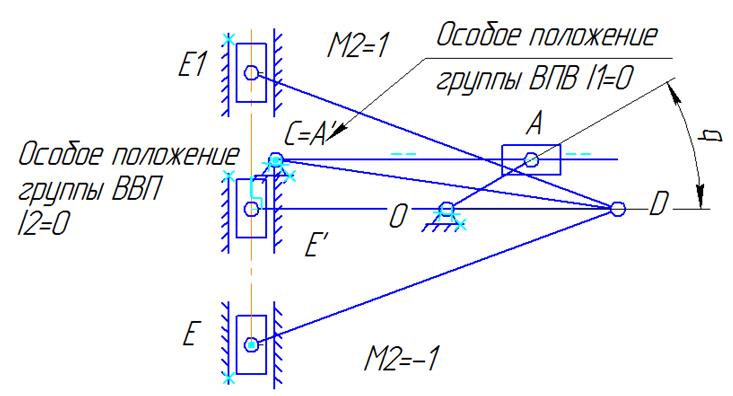
Рис. 3.5

      Особое положение механизма и способы сборки см. на рис.3.5
       Способы сборки соответствуют двум решениям тригонометрических групповых уравнений. Из одной сборки в другую можно перейти, только разобрав механизм и переставив звенья.
         В нашей работе способы сборки определяются коэффициентами М1 и М2.
         В особом положении 2 решения групповых уравнений сливаются в одно. В нем возрастают аналоги скоростей, ускорений звеньев, обобщенные уравновешивающие силы. При имеющихся исходных данных механизм не попадает в особое положение.

План 12-ти положений:

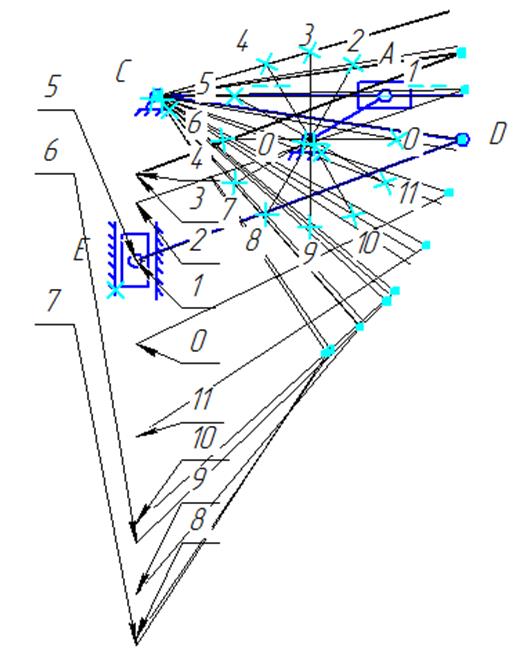
Рис. 3.6

Крайние положения:

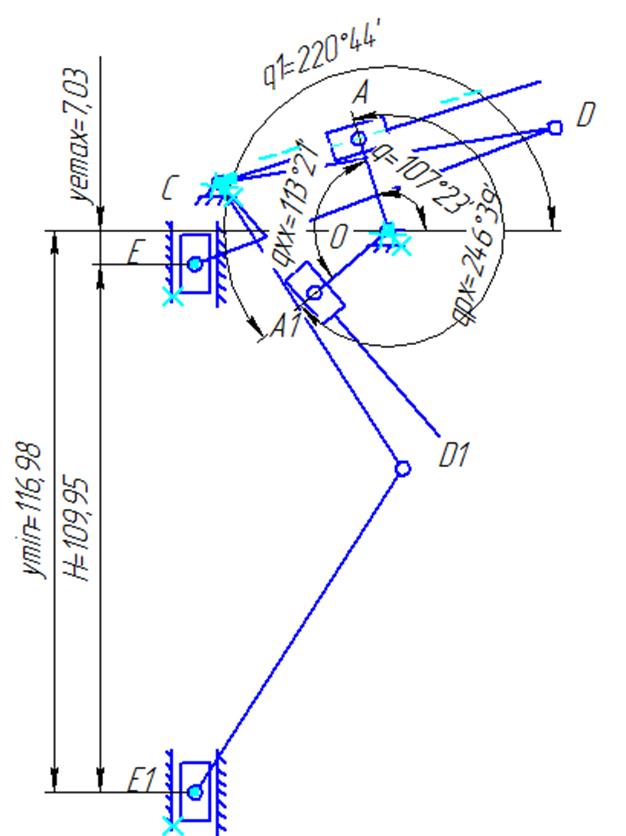
Рис. 3.7

3.4. Кинематический анализ

Выражения для производных функций положения были получены в п 2.1.4.

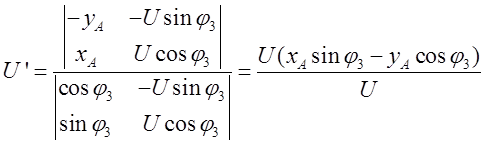
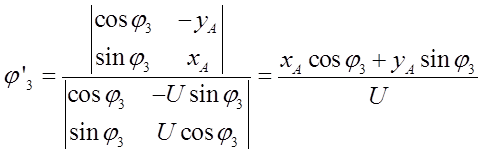
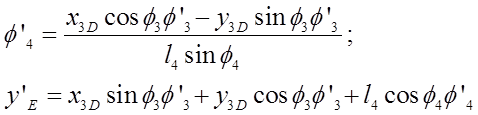
Два раза продифференцировав уравнения геометрического анализа, получим следующие выражения.

Группа ВПВ (2-3 звенья)

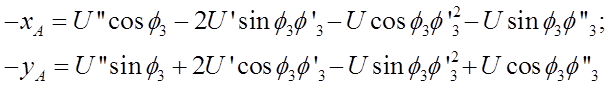
Неизвестные: , .

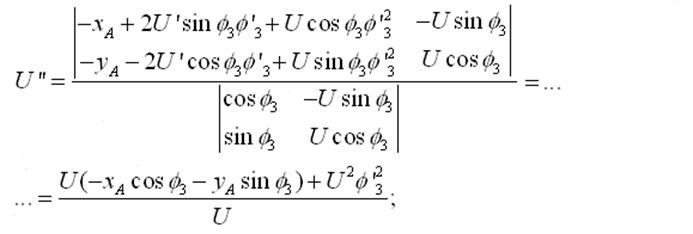
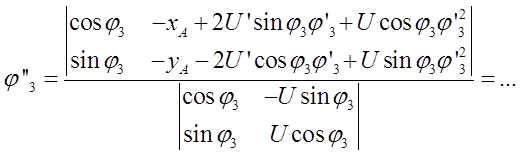
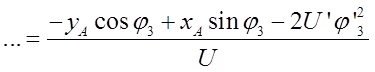
Группа ВВП(4-5 звенья)

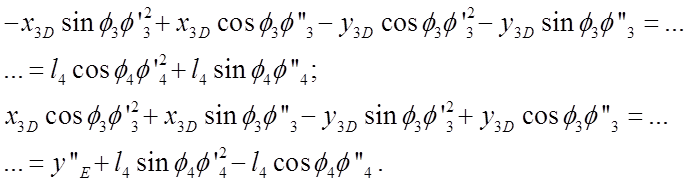
Неизвестные: ,

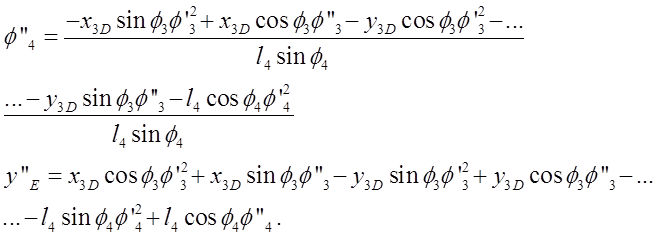
Определим скорости и ускорения графоаналитическим методом.

Свяжем с каждым звеном векторы

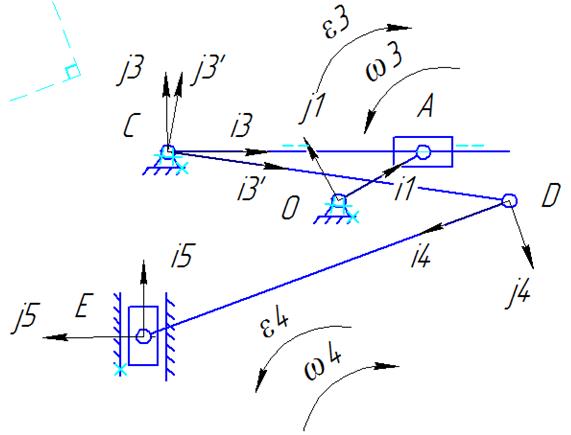
Рис. 3.8

Тогда

Продифференцировав уравнение, получим

План скоростей для заданного положения

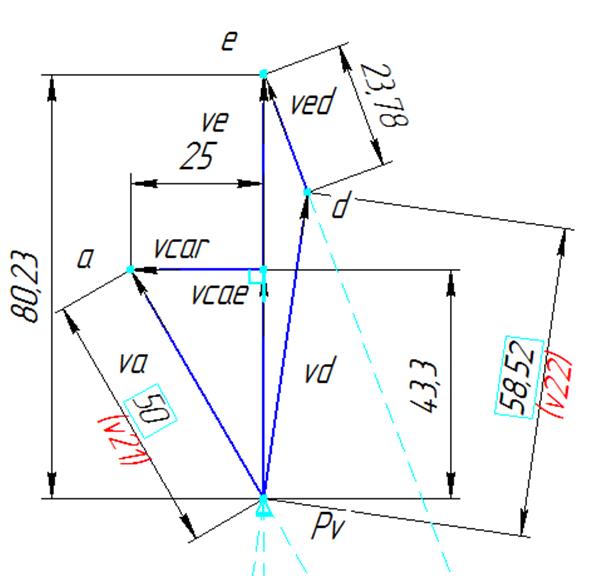
Рис. 3.9

Схема расположения звеньев механизма в крайнем положении

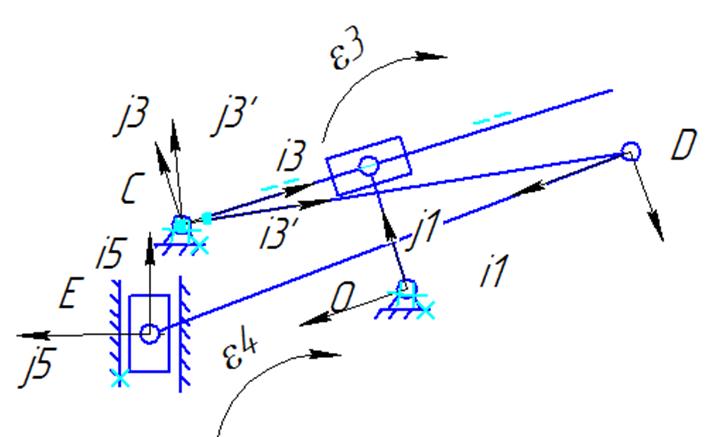
Рис. 3.10

План скоростей для крайнего положения

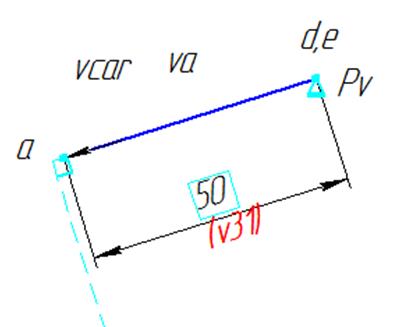
Рис. 3.11

Продифференцировав выражения для плана скоростей, получим выражения для построения плана ускорений.

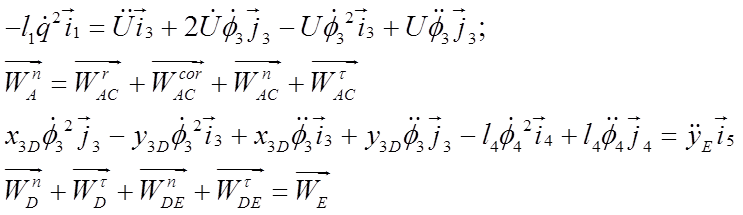
План ускорений для заданного положения

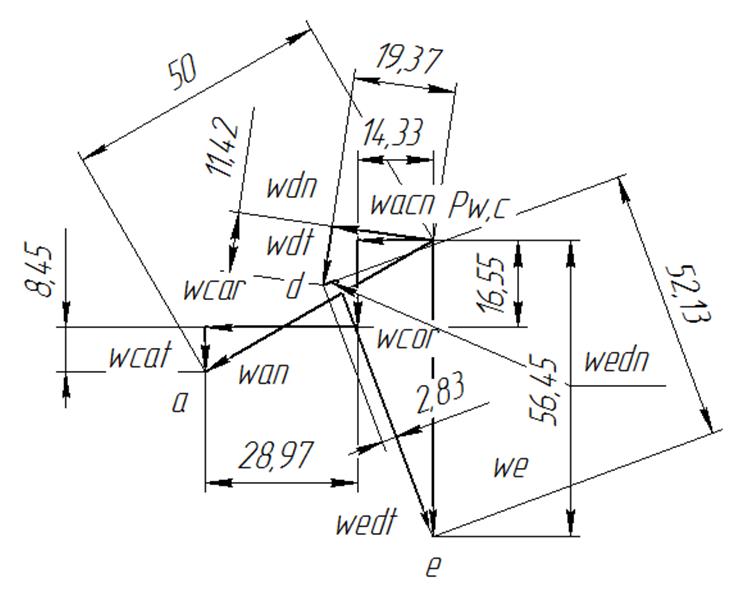
Рис. 3.12

План ускорений для крайнего положения

Рис. 3.13

Графики функции положения и ее производные выходного звена

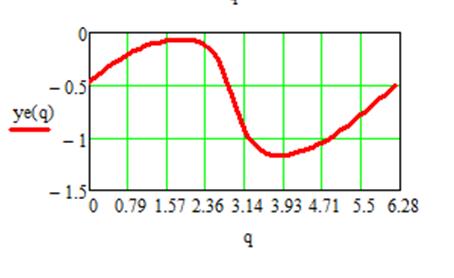
Рис. 3.14

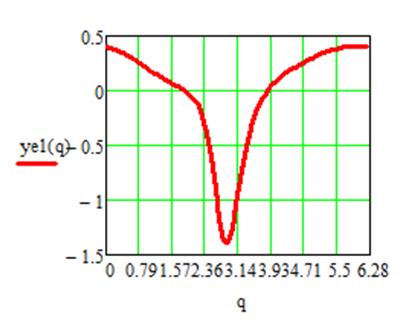
Рис. 3.15

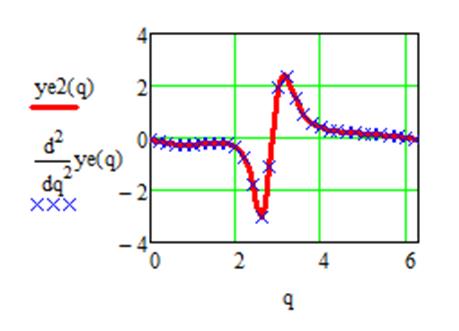
Рис. 3.16

3.5. Сравнение результатов, полученных различными методами

Точки или звенья	Координаты
	Аналитический метод		Графоаналитический метод		По программе
	X	Y	X	Y	X	Y
точка A	0.173	0.1	0.1732	0.1	0.173205	0.1
точка D	0.35	0	0.35	0	0.35	0
точка E	-0.4	-0.278	-0.4	-0.278388	-0.4	-0.278388
	φ
Звено 3	0		0		-
Звено 4	200.364		200.3641		-

1 2 3 4

Скачать файл