Детали машин. Разработка и оформление конструкторской документации курсового проекта: Учебное пособие, страница 3

            Известные рекомендации по разбивке по ступеням общего передаточного отношения для различных типов редукторов [3, 5] не вполне приемлемы, если в структуре привода, кроме редуктора, имеются, например, ременные или цепные передачи. Поэтому для учебных целей можно рекомендовать следующий способ разбивки общего передаточного отношения, основанный на одинаковой степени использования кинематических возможностей каждой из ступеней привода. Сущность способа поясним на примере. Требуется выполнить разбивку общего передаточного отношения (i_общ = 203) по ступеням привода (рис. 1.2), содержащего электродвигатель, клиноременную передачу, двухступенчатый редуктор, включающий червячную и цилиндрическую передачи. На рис. 1.3 показаны интервалы возможного изменения передаточных отношений трех ступеней данного привода (см. табл. 1.2 и примечание к ней) на трех совмещенных по границам логарифмических шкалах. Четвертая совмещенная логарифмическая шкала построена в границах, полученных перемножением соответствующих граничных значений трех верхних шкал.

                                                                                                                                                       Т а б л и ц а  1.2

Рекомендуемые значения передаточного отношения

и средние значения КПД для одной ступени привода

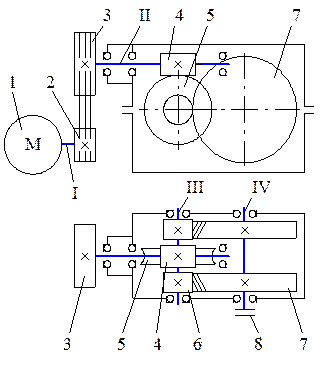
            Рис. 1.2. Кинематическая схема  привода: 1 – электродвигатель; передачи:

2, 3 – клиноременная; 4, 5 – червячная; 6, 7 – цилиндрическая зубчатая; 8 – муфта

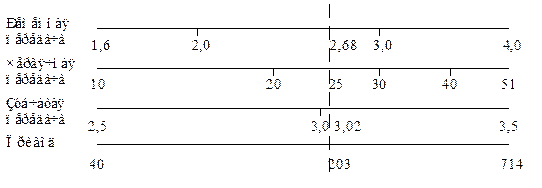
Рис. 1.3. Логарифмические шкалы для разбивки общего передаточного отношения привода

 по ступеням

            Любая вертикальная линия, проведенная через все шкалы, пересекает их в точках, соответствующих величинам передаточных отношений, связанных зависимостью

и, кроме того, в равной мере использует интервалы рациональных значений i_i каждой i-й передачи. Вертикальная линия, проведенная через заданное значение i_общ = 203 четвертой шкалы, позволяет найти соответствующие ему искомые значения

i_кл-р = 2,68; i_черв = 25,0; i_зуб = 3,02.

6

            Построение логарифмических шкал связано с определенными трудностями, поэтому значения передаточных отношений i_i каждой i-й передачи привода удобно вычислить по зависимости

,

где

            Для рассматриваемого случая

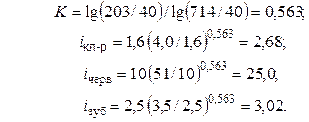
            Выполненную указанным способом разбивку общего передаточного отношения следует использовать в качестве одного из вариантов для расчета передач на ЭВМ. Для поиска рациональной конструкции привода необходим анализ других вариантов разбивки i_общ, однако он затруднен вследствие большого объема вычислений и поэтому неприемлем при курсовом проектировании.

            Так, значение передаточного отношения клиноременной передачи рекомендуется принимать по стандартному ряду передаточных отношений (см. раздел 3.1). В этом случае возможно использование стандартных шкивов, что в дальнейшем позволит ускорить процесс проектирования передачи.

            Найденные указанным выше способом значения i_i следует считать окончательными для всех передач, кроме редукторных. Варьируя передаточное отношение одной из них как независимую переменную (при неизменном передаточном отношении редуктора i_ред), следует в пределах нескольких итераций выбрать такую разбивку i_ред, при которой суммарный условный объем деталей передач  и габаритные размеры редуктора будут минимальными при соблюдении ограничений по КПД, по условиям смазывания деталей передач, по коэффициенту относительной ширины зубчатого венца y_bd и по коэффициенту осевого перекрытия зубьев e_b.