Выбор и обоснование кинематической схемы поперечно-строгалного станка

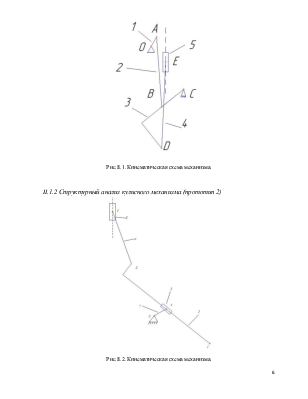
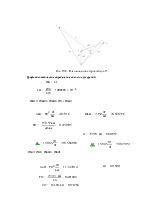
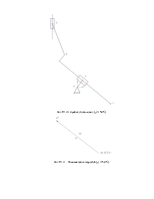
Планы скоростей и ускорений для крайних положений рассчитываются аналогично планам для положения q=60º.

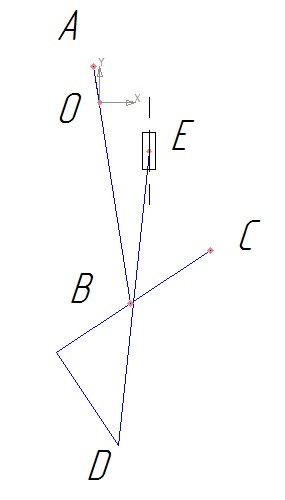
Рис. IV.4.   Крайнее положение .

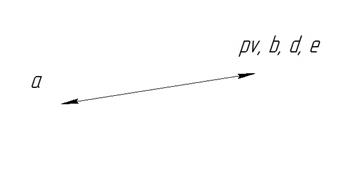
Рис. IV.5.  План аналогов скоростей .

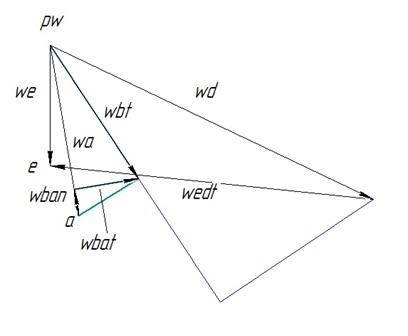
Рис. IV.6.  План аналогов ускорений

IV. 3.2 Кулисный механизм (прототип 2)

Графоаналитическое определение аналогов скоростей

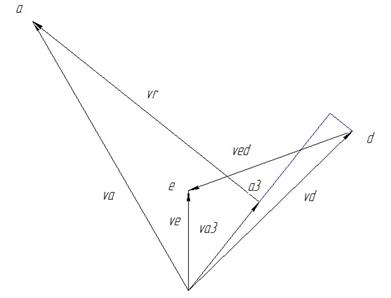
Рис. IV.8.  План аналогов скоростей q=30°.

Графоаналитическое определение аналогов ускорений.

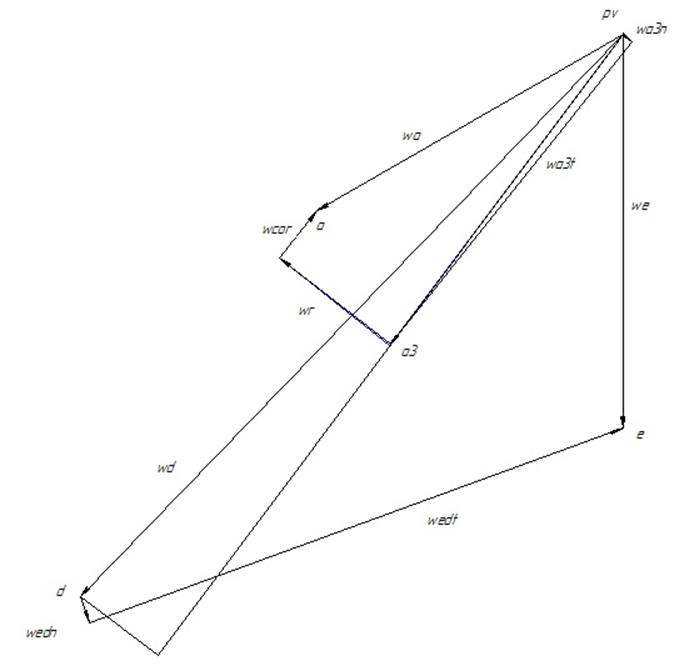
Рис. IV.9.  План аналогов ускорений q=30°.

Крайнее положение

Механизм имеет одно крайнее положение, в котором скорость точки Е равна нулю. Это положение наблюдается при значении угла 52.5º. Ниже приведены планы скоростей и ускорений для этого положения. Планы скоростей и ускорений для крайнего положения рассчитываются аналогично планам для положения q=30º.

Рис. IV.10.  Крайнее положение .

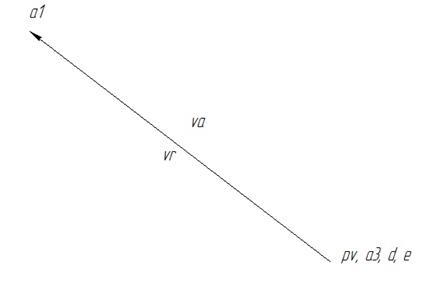
Рис. IV.11.  План аналогов скоростей .

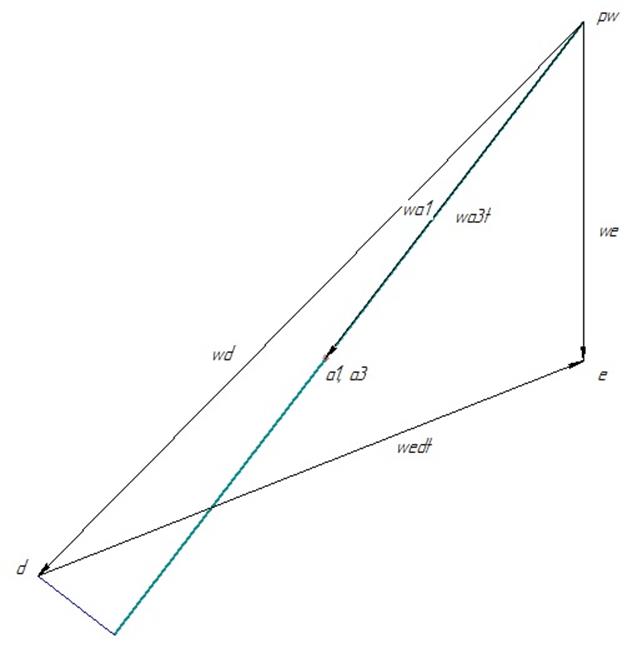
Рис. IV.12.  План аналогов ускорений .

IV. 4 Сравнение результатов, полученных различными методами для угла q=60°(прототип 1)

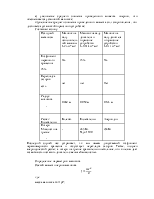
Таблица IV.1

IV. 5 Сравнение результатов, полученных различными методами для угла q=30° (прототип 2)

Таблица IV.2

IV. 6 Выводы

            Из таблиц видно, что значения скоростей и ускорений, вычисленные разными методами, совпадают. На основании проведенных исследований окончательно выбираем для дальнейших расчетов второй прототип.

V. Силовой анализ механизма

V.1 Задачи силового анализа

Основной задачей силового анализа является определение реакций в кинематических парах. Их значения необходимы, в дальнейшем, для расчета деталей на жесткость и прочность. Реакции определяются в положении, в котором действует максимальная нагрузка.

В ходе силового анализа также определяется движущий момент, который необходим для выбора двигателя механизма. Двигатель выбирается по максимальному движущему моменту и мощности. Движущий момент - тот момент, который необходимо приложить к кривошипу, для того чтобы вращать его с заданной постоянной скоростью при заданных рабочей нагрузке, силах тяжести и силах инерции.

Также необходимо оценить внутреннюю и внешнюю виброактивности механизма. Внешняя виброактивность определяется по главному вектору сил инерции. Ее можно уменьшить с помощью установки противовеса. Внутренняя виброактивность определяется по возмущающему моменту. Ее можно уменьшить с помощью установки разгружателей.

V.2 Выбор нагрузки, определение задаваемых сил и сил инерции

V.2.1 Выбор нагрузки

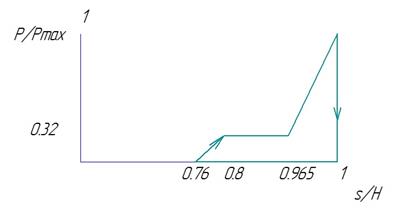
Рис.V.1. Индикаторная диаграмма.

Определение нагрузки:

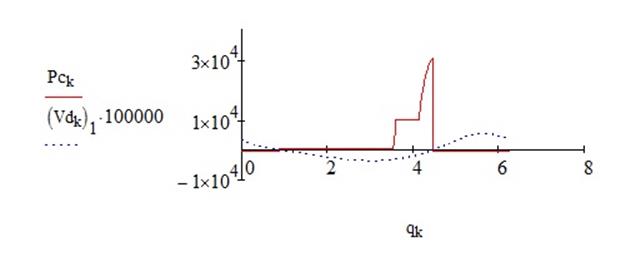
Рис.V.2. График зависимости вектора рабочей нагрузки от входной координаты.

V.2.2 Силы тяжести

Для определения масс звеньев механизма необходимо задать погонную массу.

Исходя из технического задания, погонная масса .

Момент инерции звеньев относительно центра масс рассчитывается по формуле I=ml²/12, где m-масса звена,  l-его длина.

Так же к каждому звену в центре масс приложены сила тяжести, рассчитывается по формуле G=m*g, где g = 9.8, ускорение свободного падения, m-масса каждого звена соответственно.

См. приложение-1 в MathCAD.

V.3 Составлений уравнений кинетостатики

Силовой анализ механизма аналитическим методом проводят последовательно и отдельно для каждой структурной группы, начиная с той, в которую входит выходное звено. Начальное звено анализируют последним.

Для определения реакций в кинематических парах структурных групп и начального звена составляют и решают уравнения кинетостатики.

Составляем уравнения:

Звено 5:

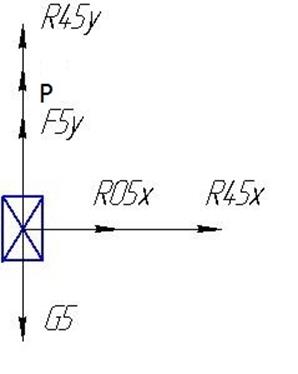
Условие равновесия звена 5:

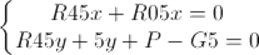
Звено 4: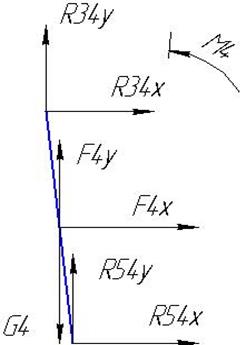

Условие равновесия звена 4:

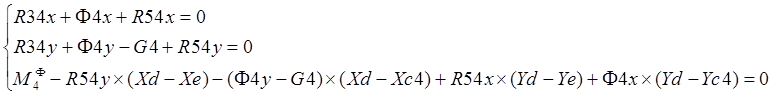
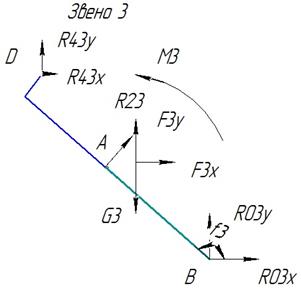
Условие равновесия звена 3:

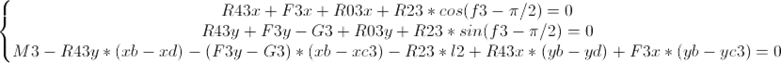
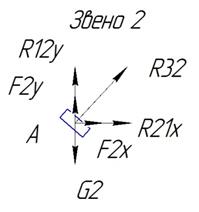
Условие равновесия камня:

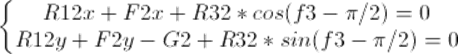
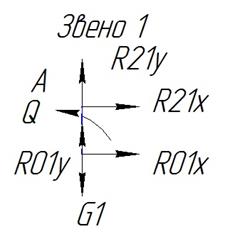
Условие равновесия кривошипа:

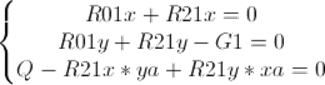
Сравнивая результаты расчета в Mathcad получаем одинаковые значения движущего момента в обоих случаях, значет вычисление были проведены верно

Рис. V.7.  Движущий момент.

V.4 Построение планов сил

Графоаналитический метод заключается в построении планов сил и определении из них реакций. Т.к. планы сил не могут учитывать действующие на механизм моменты, то необходимо силы, найденные через уравнения моментов в аналитическом решении, принять как известные.

Каждое звено механизма находится в равновесии, следовательно все силы, приложенные к нему, будут уравновешивать друг друга.

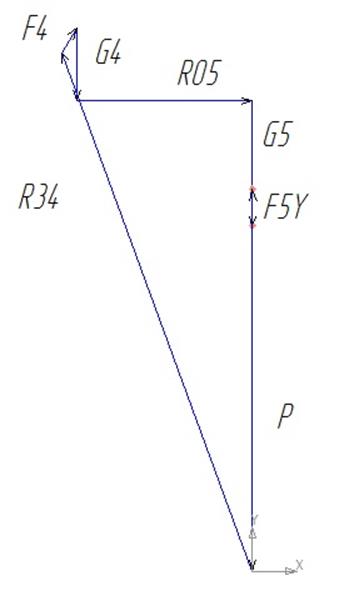
Рис. V.8.  План сил, группа ВВП.

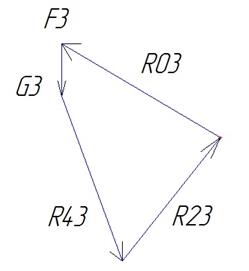
Рис. V.9. План сил звена 3.

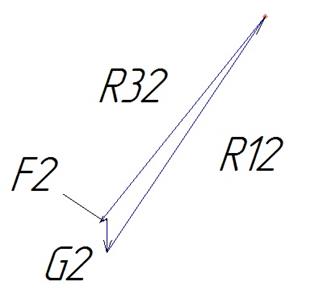
Рис. V.10. План сил звена 2.

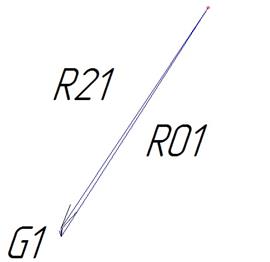
Рис. V.11. План сил, кривошип.

V.5 Сравнение силовых параметров, полученных графическим и графоаналитическим методом

V.6 Уравновешивание главного вектора сил инерции

Мерой внешней виброактивности механизма при внутренней рабочей нагрузке является главный вектор сил инерции. В цикловых механизмах он является периодической функцией и может быть разложен в сходящийся ряд Фурье, представляющий собой сумму эллиптических гармоник:

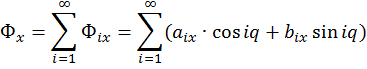
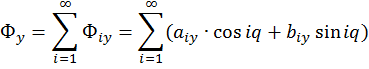
            Уравновесим первую гармонику сил инерции. Для этого нужно поставить два противовеса