Физика \ Физика

Электростатического поля точечных зарядов. Взаимодействие зарядов и заряженных тел. Сила Лоренца. Сила Ампера. Закон электромагнитной индукции Фарадея, страница 5

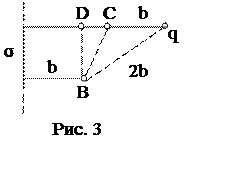
Работу перемещения найдем из формулы А = q(φ_В – φ_С). Разность потенциалов (φ_В – φ_С) равна алгебраической сумме разностей потенциалов плоскости Δφ_σ и заряда q Δφ_q. Δφ_σ, созданную плоскостью, найдем по формул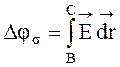е , где

Е = , 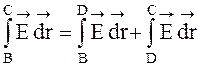. 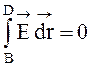(потенциалы поля, созданного плоскостью в точках D и В, равны). Теперь 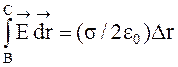, где . DC = c – b = b( – 1).

Потенциал точечного заряда вычисляется по формуле .

Тогда φ_В = , φ_С = и

Δφ_q = ;

Δφ_q = -9 ∙ 10⁹ ∙ 10^-7/(2 ∙ 0,1) = -4,5 ∙ 10³В.

Окончательно работа есть А = 10^-6 ∙ (4,14 ∙ 10³ - 4,5 ∙ 10³) = -0,36 ∙ 10³ Дж.

Ответ: А = -0,36 ∙ 10³ Дж.

Проверим размерность: [A] = [Кл] ∙ [B] = [Дж].

ЗАДАЧА 3. ОПРЕДЕЛЕНИЕ ИНДУКЦИИ

МАГНИТНОГО ПОЛЯ ТОКОВ

Найти магнитную индукцию в точке А. Номера вариантов проставлены в левом верхнем углу приведенных ниже рисунков.


I₁ = I₂ = 1 A r₁ = r₂ = 2 см		I₁ = I₂ = 0,5 A r₁ = r₂ = 2 см	I₁ = I₂ = 1 A r₁ = r₂ = 5 см

r₁ = r₂ = 2 см R₁ = R₂ = 2 см I₁ = I₂ = 1 A	r₁ = r₂ = 2 см R₁ = R₂ = 3 см I₁ = I₂ = 1 A		r₁ = r₂ = 1 см R₁ = R₂ = 2 см I₁ = I₂ = 1 A

R = 10 см I₁ = I₂ = 0,5 A	R = 1 см I₁ = I₂ = 1 A		R = 1 см I₁ = I₂ = 1 A

r₁ = r₂ = 2 см I₁ = I₂ = 1 A	1 = 4a = 20 см I₁ = 0,5 А		а = 5 см I₁ = I₂ = I₃ = 1 A

а = 2 см α = 60⁰ I₁ = I₂ = I₃ = 1 A	а = 2 см α = 60⁰ I = 1 A		а = 2 см α = 60⁰ I₁ = I₂ = I₃ = I₄ = 1 A

R = 2 см, r₁ = r₂ = 5 см I₁ = I₂ = I₃ = 1 A	r₁ = r₂ = r₃/2 = 2 см I₁ = I₂ = I₃ = 0,5 A		a = 3 см I₁ = I₂ = I₃ = 1 A

α = 45⁰, r₁ = r₂ = 5 см I₁ = I₂ = I₃ = 1 A	r₁ = 5 см r₂ = 4 см I₁ = I₂ = 0,5 A		а = 5 см I₁ = I₂ = 1 A

а = 5 см, α = 45⁰ I₁ = I₂ = I₃ = 1 A	а = 5 см, α = 45⁰ I₁ = I₂ = I₃ = I₄ = 1 A		а = 2 см, α = 45⁰ I₁ = I₃ = 2I₂ = 0,2 A

а = 5 см, I₁ = I₄ = 0,5 А I₂ = I₃ = 1 A	а = 3 см, I₂ = 4 А I₁= I₃ = 1 A

Пример решения задачи 26-го варианта

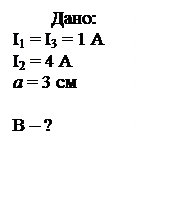
Подпись: Дано:
I1 = I3 = 1 A
I2 = 4 A
а = 3 см

В – ?

Решение:

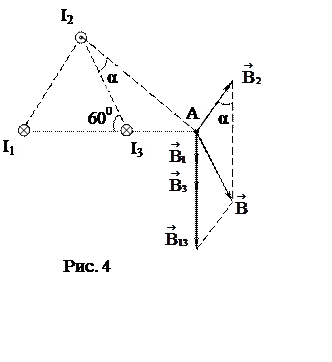
Покажем направления векторов индукции магнитных полей. Магнитные поля В₁ и В₃, направленные одинаково, найти просто по формуле для бесконечно длинного прямолинейного проводника:

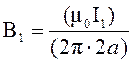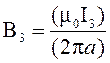Магнитные поля подчиняются принципу суперпозиции. Поэтому равнодействующая полей В₁, В₂

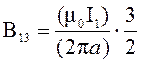Для нахождения В₂ надо знать расстояние до точки А от тока I₂. Его, например, найдем по теореме косинусов . Теперь 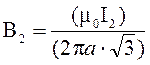. Построив равнодействующую из векторов В₂ и В₁₃, найдем ее длину. Вновь по теореме косинусов

где α = 30⁰, как нетрудно найти.

С учетом того, что I₂ = 4I₁, получаем

;

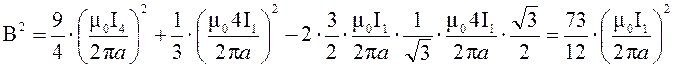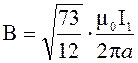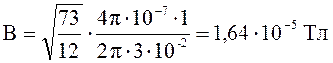Ответ: В = 16,4 мкТл.

Проверка размерности достаточно очевидна.

ЗАДАЧА 4. СИЛА ЛОРЕНЦА, СИЛА АМПЕРА,

ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ ФАРАДЕЯ

Примечание: в вариантах, в которых рассматривается α-частица, считать ее массу равной четырем массам протона. Заряд α-частицы равен по модулю двум зарядам электрона.

1. В однородном магнитном поле с индукцией В = 100 мкТл по винтовой линии движется электрон. Определить его скорость вращения, если шаг h винтовой линии равен 20 см, а радиус вращения R = 5 см.

Ответ: 1,04 ∙ 10⁶ м/с.

2. В однородном магнитном поле с индукцией В = 20 мкТл по винтовой линии движется электрон. Электрон влетел в поле под углом 30⁰ к силовым линиям, имея импульс р = 10^-24 кг∙м/с. Найти радиус вращения электрона. Ответ: 0,16 м.

3. Электрон влетает в однородное магнитное поле под углом 45⁰ к силовым линиям, имея энергию W = 5,5 ∙ 10^-19 Дж. Магнитная индукция В = 10 мкТл. Найти радиус вращения электрона. Ответ: 0,44 м.

1 2 3 4 5 6 7

Скачать файл