Электростатического поля точечных зарядов. Взаимодействие зарядов и заряженных тел. Сила Лоренца. Сила Ампера. Закон электромагнитной индукции Фарадея, страница 3

Пример решения 26-го варианта

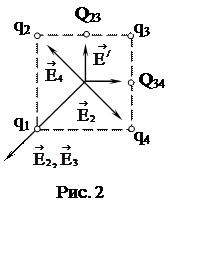
В вершинах квадрата со стороной а = 10^{-2 м расположены заряды}       q₁ = -5 ∙ 10^-9 Кл, q₂ = q₄ = 10^-9 Кл, q₃ = 5 ∙ 10^-9 Кл и неизвестные заряды Q₂₃, Q₃₄, равные между собой (рис. 2). Поле в центре квадрата равно нулю. Найти Q₂₃, Q₃₄.

Дано:                                               Решение:

q₁ = -5 ∙ 10^-9 Кл                                                      Модуль вектора напряжен-

q₂ = q₄ = 10^-9 Кл                                               ности  точечного заряда q вы-  

q₃ = 5 ∙ 10^-9 Кл                                                 числяется по формуле

а = 10^{-2 м}                                                                             Е = k ∙ |q|/r²,

                                                                          где k = 9 ∙ 10⁹ Н ∙ м²/Кл².

Q₂₃, Q₃₄ – ?                                                       Электростатические  поля  под-

                                                                          чиняются принципу суперпози-

                                                                          ции, согласно которому результи-

                                                                          рующий   вектор  напряженно-

                                                                          сти поля, созданного несколькими зарядами, равен векторной сумме напряженностей отдельных зарядов.

Теперь покажем направления векторов напряженностей, создаваемых  зарядами q₂ и q₄.  Так как эти заряды равны, то и || = ||,  т. е. равнодействующая  их равна 0.

Вектор напряженности, создаваемой зарядом q₃, направлен от заряда q₃ в сторону заряда q₁. Поскольку q₃ = q₁, то эти векторы ,  равны. Таким образом, напряженность, создаваемая зарядами q₁. …, q₄ фактически равна 2Е₁ и вектор направлен к заряду q₁. Так как результирующая напряженность в центре квадрата по условию равна нулю, то это означает, что заряды Q₂₃  и Q₃₄ должны быть отрицательны. Их результирующая напряженность Е_Q должна быть равна 2Е₁ и вектор  должен быть направлен противоположно вектору 2

 = – 2.

Так как Q₂₃  =  Q₃₄, то их напряженности по модулю равны между собой. Как легко видеть Е_Q = , где E^/  есть напряженность, создаваемая зарядом Q₂₃. Итак,  ,   , и далее 

 = .

Отсюда выражаем |Q₂₃|

,     ,   .

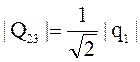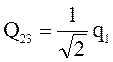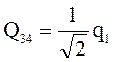Подставляя численные данные,  получаем ответ.

Ответ:  .

Проверка размерности очевидна.

ЗАДАЧА 2. ВЗАИМОДЕЙСТВИЕ

ЗАРЯДОВ И ЗАРЯЖЕННЫХ ТЕЛ

Заряд Q находится на расстоянии b от одного из заряженных тел. При перемещении заряда Q из точки В в точку С совершается работа, т. к. разность потенциалов этих точек отлична от нуля. Точки В и С лежат в одной плоскости с бесконечно длинной нитью (с обеими нитями) и также в одной плоскости с центрами заряженных шаров или обоими точечными зарядами.

Во всех вариантах необходимо найти работу перемещения заряда Q между точками В и С. Исходные данные к этой задаче даны в табл. 3, 4.

Таблица 3

Исходные данные к задаче по теме № 2

Продолжение табл. 3