Определение вероятности того, что две наиболее сильные команды окажутся в одной подгруппе. Расчет вероятности выбора детали первого сорта. Расчет вероятности допущенной ошибки

наудачу выбранная из изготовленных в цехе  деталь окажется изделием первого сорта.

Решение

Обозначим события: .

А = {производство стандартной детали}

B={производство детали первого сорта}

По условию:

,         ,

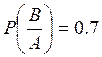Отсюда

В данном случае B может осущетвиться только одновременно с осуществлением события А, то есть   По теореме умножения вероятностей:

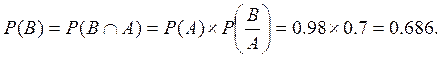
Таким образом, вероятность производство первого сорта раина 0,868.

Ответ: 0,868

                               Задача№4

Электрическая цепь на участке MN собрана по схеме, изображенной на рисунке. Каждый из элементов e1 – e7 выходит из строя независимо от других. Надежность (вероятность безотказной работы в течение заданного промежутка времени) каждого из элементов равна 0,9. Предполагая, что сбой в цепи может произойти только вследствие нарушения функционирования элементов e1 – e7, найти надёжность участка цепи MN.

                                                       

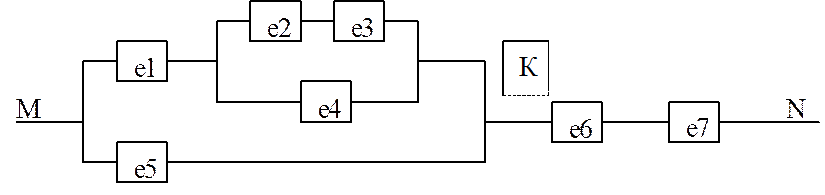
Решение

Обозначим события

безотказная работа i-го элемента в течении времени T}

i=1,2…7;

{безотказная работа в течении времени T участка цепи NK}

C- {безотказная работа всего участка цепи MK в течении времени T}

D- {одновременно безотказная работа  ,  и функционирование }

Событие  С представим в виде , то есть для функционирования участка  цепи MK необходимо безотказное функционирование участков MKи KN.

Для обеспечения функционирования участка MN необходимо хотя бы одно условие:

1.  Безотказная работа элемента

2.  Безотказная работа элемента  и одновременно безотказная работа ,  и  функционирование .

Для определения вероятности  применяем теорему сложения вероятностей совместных событий и теорему умножения вероятностей независимых событий.

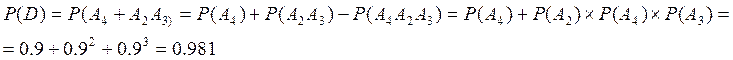
Для функционирования участка KN необходима безотказная работа элементов  и .

Для вычисления вероятности   перейдем к рассмотрению события , состоящего в отказе цепи KN. Для  осуществления события   необходим одновременный выход из строя  хотя бы одного из элементов  или .

Учитывая, что события   и - совместны получим:

,

где  .

Отсюда

Окончательно вероятность события С:

Ответ: 0,7276

                                Задача№5

      Вероятность того, что при одном измерении некоторой физической величины будет допущена ошибка, превышающая заданную точность, равна 0,4. Произведены три независимых испытания. Найти вероятность того, что только в одном из них допущенная ошибка превысит заданную точность. Р=0,432

                                                      Решение

Е: производят измерения некоторой физической величины.

А={ошибка превысит заданную точность в первом эксперименте}

В={ошибка превысит заданную точность во втором эксперименте}

С={ошибка превысит заданную точность в третьем эксперименте}

D={ошибка превысит заданную точность в}

P(D)-?

P(A)=0.4

P(B)=0.4

P(C)=0.4

Т.к. события ,  и   не совместны, а события А, В и С не зависимы, то вероятность наступления события D по теореме сложения вероятностей:

Ответ: Р(D)=0.432

Задача№6

Вероятности того, что во время работы ЭВМ возникает сбой в арифметическом устройстве, в оперативной памяти, в остальных устройствах, соотносятся так: 3:2:5. Вероятности обнаружения сбоя в арифметическом устройстве, в оперативной памяти и в остальных устройствах соответственно равны 0,8;0,9;0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен. Р=0,87

                                                      Решение

Е: испытание ЭВМ

А={сбой будет обнаружен в ЭВМ }

В={сбой произойдет и будет обнаружен в арифметическом устройстве }

С={сбой произойдет и будет обнаружен в оперативной памяти}