Задача 2
Расчёт вероятности нарушения безопасности движения поездов
1. По заданным значениям реализованного числа единичных маршрутов (N=100), числу нарушений безопасности единичного маршрута (n=9), вероятности нарушения безопасности единичного маршрута (QЕМ=1,9×10-6) найти вероятность нарушений безопасности n маршрутов (Qn). Выполнить расчёты по формулам биноминального и пуассоновского закона распределений, сравнить результаты расчётов и сделать соответствующие выводы.
Зная вероятность НБФ единичного маршрута, нетрудно определить вероятность нарушений безопасности при реализации ряда этих маршрутов. На основании этого можно дать количественную оценку уровня безопасности движения на полном маршруте, диспетчерском круге, отделении дороги, на дороге.
Используем формулу биноминального закона распределений:
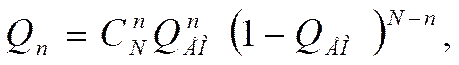 (1)
(1)
где N – число единичных маршрутов,
n – число НБФ единичного маршрута;
число сочетаний из N по n
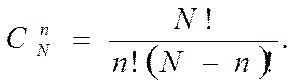 (2)
(2)
Подставляя исходные данные в формулы (1) и (2) получим:
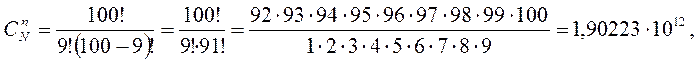
![]()
Используем формулу пуассоновского закона распределений:
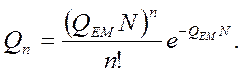 (3)
(3)
Подставляя исходные данные в формулу (3) получим:
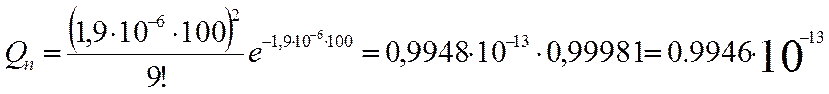
2 Заданы интенсивность потока нарушений безопасности единичного маршрута l=2,9×10-5 1/ч; среднее время единичного маршрута t0=2,1 ч; среднее время реализации ряда маршрутов tс=210 ч. Определить: вероятность нарушения безопасности при реализации одного единичного маршрута Qем; вероятность того, что при реализации ряда (N) маршрутов произойдёт не менее одного (Qn³1), не менее двух (Qn³2) нарушений безопасности.
Множество единичных маршрутов N реализуется за время tс, поэтому
N=tc/t0,
где t0 – средняя продолжительность одного единичного маршрута, ч.
Отсюда
N=210/2,1=100 маршрутов.
Учитывая, что с одним и тем же поездом за время единичного маршрута не может произойти более одного нарушения безопасности, математическое ожидание mНБО числа нарушений безопасности в течении t0 можно записать
mНБО=lt0=1Qем=Qем,
где l - интенсивность потока нарушений безопасности, т. е. их среднее число в
единицу времени t0, 1/ч.
Следовательно
Qем=2,9×10-5×2,1=6,09×10-5.
Вероятность (Qn³1) того, что при реализации N единичных маршрутов произойдёт хотя бы одно нарушение безопасности движения за определённое время, выразим:
(Qn³1)=1-Qn=0.
В свою очередь, вероятность (Qn³2) того, что произойдёт два и более нарушения безопасности в N маршрутах будет равна
(Qn³2)=1-Qn=0- Qn=1.
Пуассоновское распределение числа нарушений безопасности имеет вид
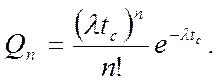
Отсюда
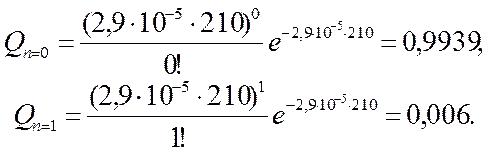
Следовательно
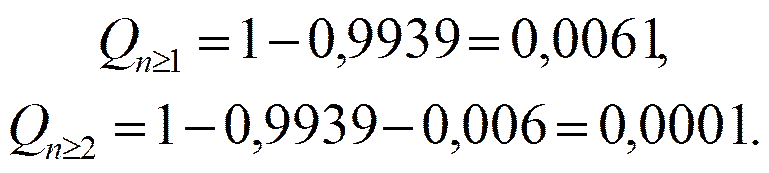
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.