Методические указания к выполнению задачи «Применение статистических методов в исследовании качества продукции и технологических процессов»

Методические указания к выполнению задачи

«Применение статистических методов в исследовании качества продукции и технологических процессов»

Взяв выборку из генеральной совокупности и вычисляя статистические характеристики этой выборки –  и S, можно с некоторой приближенностью считать, что эти характеристики по своим величинам будут близки к соответствующим параметрам генеральной совокупности – .

Если

,

где  – среднеарифметические значения случайной величины соответственно в генеральной совокупности и в выборке объема n;  – среднеквадратичные отклонения изучаемой величины соответственно генеральной совокупности и в выборке из нее, то по заданной точности и вероятности приближенного равенства  можно определить необходимый объем выборки

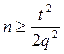,                                                              (1)

где t и q – параметры вероятности и приближения модели (таблица 2.1 задания).

Студенты, в зависимости от своего варианта, определяют выборку из общей совокупности данных (таблица 2.2 задания) и сводят ее в таблицу.

Обработка статистической информации

Находятся наибольшее  и наименьшее  значения наблюдаемого параметра X (загрузка вагона, т).

Размах варьирования загрузки или широта распределения при этом составляет

R =  –                                                        (2)

Число интервалов определяется по формуле Стерджесса:

Цена интервала, при этом, составит

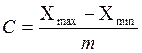                                                      (3)

Подсчет частоты варьируемой величины (загрузки вагона) по каждому интервалу удобно производить следующим способом. В один из столбцов таблицы выписываются интервалы от X_min до X_min + C; от X_min + C до X_min + 2C и т.д. В каждый интервал включают полученные значения выборки, лежащие в пределах от наименьшего значения интервала включительно, до наибольшего значения интервала исключительно. Справа при помощи черточек можно подсчитывать число размеров по интервалам (таблица 1).

Таблица 1 – Расчет размеров по интервалам

По данным таблицы 1 вычерчивается эмпирическая (экспериментальная) кривая распределения (по оси абсцисс откладывают середины интервалов, по оси ординат – частоты). На основании таблицы частот и эмпирической кривой распределения выдвигается гипотеза о распределении случайной величины (рисунок 1).

В нашем случае может оказаться правомерной гипотеза о нормальном распределении, которое часто применяется при решении задач математической статистики и статистического контроля качества на водном транспорте. Такое распределение свидетельствует об устойчивости процесса, так как значительные отклонения от номинальных значений встречаются редко.

Выдвинутую гипотезу необходимо проверить.

Чтобы найти и проверить закон распределения рассчитываются числовые характеристики:

• среднеарифметическое отклонение загрузки вагона

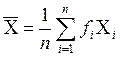                                                      (4)

• среднеквадратичное отклонение исследуемой величины

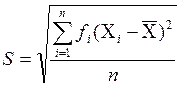                                               (5)

где п – объем выборки;  – середина интервала (из таблицы 1).

При наличии обширных данных (объемной выборки) вычисление среднеарифметического значения загрузки вагона и среднеквадратичного отклонения этой величины весьма трудоемко, на практике, для расчета этих статистических характеристик, рекомендуется составлять таблицу предварительной обработки данных (таблица 2).

Таблица 2 – Расчет статистических характеристик измеряемых величин