Рабочая программа дисциплины "Численные методы" для специальности "Программное обеспечение вычислительной техники и автоматизированных систем"

                                                                           к.ф.-м.н.

                                                                          __________________Н.Е.Амандус

Автор  :           д.ф.-м.н., доцент С. Б. Сорокин

Рецензент:     д.ф.-м.н., профессор А.Ф. Воеводин

     
1. Пояснительная записка

Данная дисциплина рассматривается как обязательная дисциплина прикладного характера, определяющая специализацию студента.

Методы и приемы математического аппарата, изучаемые студентами в рамках данной дисциплины, имеют непосредственное приложение в профессиональной деятельности выпускников Колледжа и необходимы для решения ими практических задач, связанных с математическим моделированием в различных областях знаний.

В качестве основы курса преподаются основополагающие принципы вычислительной математики, дающие студентам необходимый объем знаний для численного решения практических задач численного анализа, линейной алгебры, обыкновенных дифференциальных уравнений и обработки информации. К концу изучения данной дисциплины, студенты должны владеть приемами решения задач алгебраического интерполирования функций, заданных аналитически или таблично, численного интегрирования и дифференцирования функций, вычисления корней нелинейных уравнений, нахождения решения системы линейных алгебраических уравнений и задачи Коши для обыкновенных дифференциальных уравнений.

На протяжении всего курса большое внимание уделяется решению упражнений и задач по изучаемым в рамках преподаваемой дисциплины разделам и темам, что позволяет студентам последовательно осваивать различные подходы к решению практических задач и глубже понимать природу и специфику численных методов.

Контроль по данной дисциплине осуществляется в форме экзамена и/или зачета, которые проводятся после окончания изучения дисциплины, и потоковых контрольных работ, проводимых два раза в семестр.

     
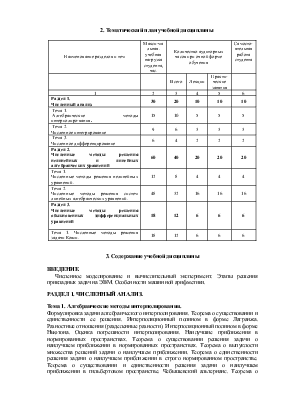
2. Тематический план учебной дисциплины

3. Содержание учебной дисциплины

ВВЕДЕНИЕ.

Численное моделирование и вычислительный эксперимент. Этапы решения прикладных задач на ЭВМ. Особенности машинной арифметики.

РАЗДЕЛ 1. ЧИСЛЕННЫЙ АНАЛИЗ.

Тема 1. Алгебраические методы интерполирования.

Формулировка задачи алгебраического интерполирования. Теорема о существовании и единственности ее решения. Интерполяционный полином в форме Лагранжа. Разностные отношения (разделенные разности). Интерполяционный полином в форме Ньютона. Оценка погрешности интерполирования. Наилучшие приближения в нормированных пространствах. Теорема о существовании решения задачи о наилучшем приближении в нормированных пространствах. Теорема о выпуклости множества решений задачи о наилучшем приближении. Теорема о единственности решения задачи о наилучшем приближении в строго нормированном пространстве. Теорема о существовании и единственности решения задачи о наилучшем приближении в гильбертовом пространстве. Чебышевский альтернанс. Теорема о чебышевском альтернансе. Многочлен Чебышева, наименее уклоняющийся от нуля. Выбор узлов интерполирования.

Тема 2. Численное интегрирование.