Исследования машинного агрегата и проектирование редуктора (среднее удельное давление на поршень насоса = 0,32 МПа, средняя скорость поршня насоса = 0,28 м/с)

давления жидкости в цилиндрах насоса на поршни при прямых и обратных ходах. Они характеризуются средним постоянным удельным давлением Р.

Сила постоянного давления F,(Н) на поршень определяем по формуле:

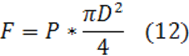
где   – площадь поршня насоса, м² ; D – диаметр поршня, м; Р – среднее удельное давление, МПа.

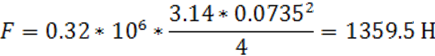
Располагая значением силы давления F в цилиндрах насоса, можно определить приведенные моменты сил Т_пр1(j) для первого КПМ и Т_пр2(j) для второго КПМ.

При изменении направления скорости движения поршня изменяется и направление силы давления на поршень. Однако, учитывая, что оба хода поршня являются рабочими, при определении приведенных моментов принимаем абсолютные значения скорости и силы давления на поршень.

Значения приведенных моментов сил давления определяем по формулам:

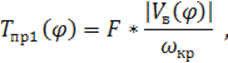
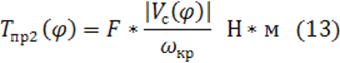
При определении приведенных моментов сил Т_пр1(j) и Т_пр2(j) пренебрегаем силами тяжести звеньев, в силу их малости по сравнению с силами давления жидкости на поршни насосов.

Суммарный приведенный момент сил производственных сопротивлений для каждого значения угла j поворота кривошипа представляет собой сумму производственных моментов сил давления жидкости на поршни двух КПМ:

Значение Т_пр.ср за один цикл движения определяем по формуле:

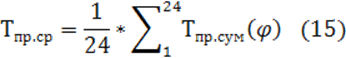
Результаты расчетов приведенных моментов при изменении угла поворота кривошипа сводим в таблицу. По данным расчета строим диаграммы приведенных моментов при изменении угла поворота кривошипа в пределах от нуля до 360⁰.

№ п/п	j градусы	Vв(j)	Vс(j)	Тпр1(j) Н×м	Тпр2(j) Н×м	Тпр.сум(j) Н×м	Тпр.ср Н×м
1	0	0	-0.4398	0	65	65	84.9898
2	15	-0,1413	-0,3973	20,88	58,72	79,6
3	30	-0,2675	-0,3333	39,53	49,25	88,79
4	45	-0,366	-0,256	54,08	37,83	91,92
5	60	-0,4285	-0,1723	63,32	25,46	88,79
6	75	-0,4523	-0,08635	66,84	12,76	79,6
7	90	-0,4398	0	65	0	65
8	105	-0,3973	0,08635	58,72	12,76	71,48
9	120	-0,3333	0,1723	49,25	25,46	74,71
10	135	-0,256	0,256	37,83	37,83	75,67
11	150	-0,1723	0,3333	25,46	49,25	74,71
12	165	-0,08635	0,3973	12,76	58,72	71,48
13	180	0	0,4398	0	65	65
14	195	0,08635	0,4523	12,76	66,84	79,6
15	210	0,1723	0,4285	25,46	63,32	88,79
16	225	0,256	0,366	37,83	54,08	91,92
17	240	0,3333	0,2675	49,25	39,53	88,79
18	255	0,3973	0,1413	58,72	20,88	79,6
19	270	0,4398	0	65	0	65
20	285	0,4523	-0,1413	66,84	20,88	87,73
21	300	0,4285	-0,2675	63,32	39,53	102,9
22	315	0,366	-0,366	54,08	54,08	108,2
23	330	0,2675	-0,4285	39,53	63,32	102,9
24	345	0,1413	-0,4523	20,88	66,84	87,73
25	360	0	-0,4398	0	65	65

4.2 Определение мощности сил движущих и подбор электродвигателя

Мощность сил движущих определяем по формуле:

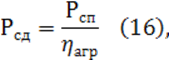
где Р_сп – мощность сил производственных сопротивлений, кВт;

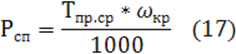
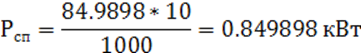
h_агр – КПД машинного агрегата без учета потерь в двигателе (собственные потери двигателя учитываются в его выходных параметрах).

КПД агрегата оценивается приблизительно с учетом типа соединения редуктора и насоса:

h_агр = h_рп ×h_р ×h_н ×h_м , (18)

где h_рп – КПД ременной передачи, h_агр =0,92…0,96;

h_р – КПД цилиндрического редуктора, h_р =0,96;

h_н – КПД насоса (при параллельном соединении кривошипно-ползунных механизмов насоса h_н =0,9);

h_м – КПД соединительной муфты, h_м =0,98.

h_агр =0,93×0,96×0,9×0,98 = 0,787

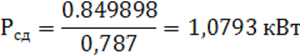
Требуемую мощность электродвигателя рассчитываем по формуле, кВт:

По мощности Р_эл и заданной угловой скорости вращения w_эл из Приложения А выбираем тип электродвигателя, его номинальную мощность, скорость вращения вала n_ном . Для дальнейших расчетов выписываем момент инерции J_р ротора, диаметр выходного вала d_вых электродвигателя.

Тип электродвигателя: АОЛ2-22-4;

номинальная мощность электродвигателя: Р_ном = 1.5 кВт;

скорость вращения вала:  n_ном = 1420 об/мин = 149 рад/с;

момент инерции ротора:  J_р = 0,011 кг*м² ;

диаметр выходного вала электродвигателя: d_вых = 22 мм.

4.3. Приведение моментов инерции звеньев агрегата к валу кривошипа

Приведенный к валу кривошипа момент инерции звеньев определяют по формуле:

где: J_о – средний, приведенный к валу кривошипа момент инерции кривошипно-ползунного механизма (J_о≈ 0,1…0,3 кг× м)

J_к, J_ш – моменты инерции колеса и шестерни, кг м;

J_б, J_т - моменты инерции быстроходного и тихоходного валов редуктора,

кг ×м;

J_эл - момент инерции ротора электродвигателя, определяемый из каталога по маховому моменту,

J_эл =0,011 кг×м,

Момент инерции колес определяется приближенно по формуле:

 где: b – ширина зубчатого колеса, м

d – диаметр делительной окружности колеса, м

 - плотность материала зубчатого колеса (для стали =7,8*10кг/м)

Моменты инерции валов оценивают приближенно по формуле:

где:  d- эквивалентное значение диаметра, м, приближенно d=d(посадочный  диаметр вала под подшипники);

l -длина вала, (быстроходного – 148мм, тихоходного – 185 мм)

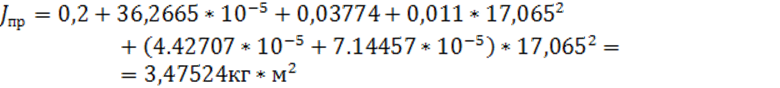
4.4. Определение момента инерции маховика

Момент инерции маховика определяют по формуле:

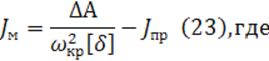
 - избыточная работа, Дж

 - допускаемое значение коэффициента неравномерности вращения коленчатого вала.

Максимальную избыточную работу находим по диаграмме приведенных моментов путем подсчета избыточной площади  и умножаем ее на масштабные коэффициенты КиК:

К - масштабный коэффициент оси моментов сил, Нм/мм

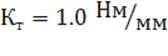
К - масштабный коэффициент углов поворота, рад/мм.

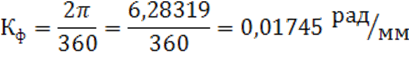
=979,6455 мм

4.  Расчет зубчатого редуктора

4.1  Определение допускаемых напряжений

   Расчет зубчатых колес редуктора производим из условий обеспечения прочности зубьев по контактным напряжениям:

s_н £ [s_н].  (25)

Допускаемые контактные напряжения при расчете на выносливость:

[s_н] =  × Z_н ,  (26)

где s_нlim – предел контактной выносливости поверхностей зубьев, МПа;

S_н – коэффициент безопасности;

Z_н – коэффициент долговечности.

Приближенное значение предела контактной выносливости при заданной твердости поверхности зубьев НВ£350 определяем из выражения:

s_нlim = 2НВ + 70  (27)

s_нlim = 2×225 + 70 = 520

При заданной долговечности редуктора L = 10000 ч величина Z_н = 1, а коэффициент безопасности зависит от термообработки зубчатых колес. При нормализации или улучшении рекомендуется значение S_н = 1,1.

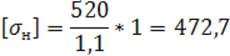
[s_н] =  × 1 = 472,7

s_н принимаем равным 470

4.2  Расчет цилиндрической косозубой передачи

Межосевое расстояние определяем по формуле [28], мм:

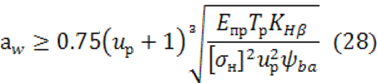
где Е_пр – приведенный модуль упругости материала зубчатых колес, (Е_пр = 2,1×10⁵ МПа);

Т₂ – вращающий момент на колесе, Н×мм;

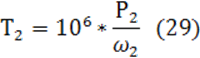
здесь Р₂ – мощность, передаваемая колесом, кВт;

– угловая скорость вращения колес,  , рад/с;

 

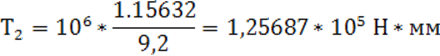
К_нb - коэффициент концентрации нагрузки, К_нb= 1…1,15;

y_ba – коэффициент ширины колеса относительно межосевого расстояния, y_ba = 0,3…0,5.

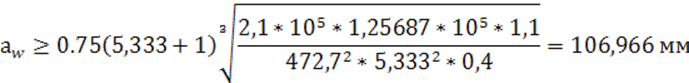
Величину межосевого расстояния а_w округляем до ближайшего значения из ряда Rа 40 по ГОСТ 6636-69 (Rа 40…80; 85: 90; 95; 100; 105; 110; 120; 125; 130 мм, далее через 10 до 260). Величину межосевого расстояния а_w округляем до 110 мм.

Приближенное значение нормального модуля определяем из выражения:

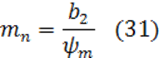
где b₂ – ширина зубчатого колеса, мм;

y_m – коэффициент ширины колеса по модулю, y_m = 20…30.

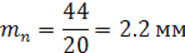
Величину модуля m_n округляем до ближайшего большего значения (по ГОСТ 9563-60 m_n = 1; 1,25; 1,5; 2; 2,25; 3; 3,5; 4; 4,5; 6; 8; 10). Величину модуля m_n округляем до 2,25 мм.

Предварительно угол наклона зуба β рассчитываем по формуле:

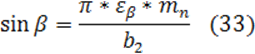
где e_β – коэффициент осевого осевого перекрытия, рекомендуется принять  e_β = 1,2.

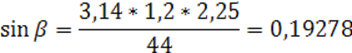
Значение угла β наклона зуба принимаем в пределах 8⁰ ≤ β≤ 20⁰.

Значение угла β наклона зуба принимаем равным 11⁰.

Суммарное число зубьев шестерни и колеса:

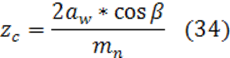
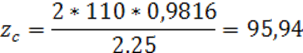
Полученное значение z_с округляем в меньшую сторону до целого числа; z_с =95.

Число зубьев шестерни:

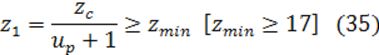
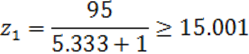
Полученное значение z₁ округляем до ближайшего значения; z₁ = 16.

Число зубьев колеса:

Окончательное значение угла β (с точностью до 1^') определяем по формуле:

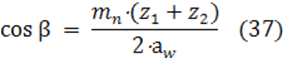
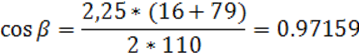
Угол β = 13^о41^'.

Диаметры делительных окружностей шестерни и колеса, мм:

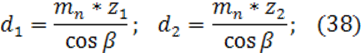
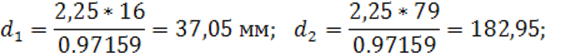
Ширина шестерни:

5.3 Проверочный расчет по контактным напряжениям

Расчет прочности зубьев по контактным напряжениям для цилиндрической косозубой передачи  выполняется по формуле:

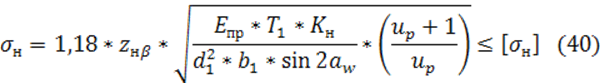
где: z_нβ- коэффициент контактной прочности косозубых передач по контактным напряжениям равен ≈ 0,85;

        Т – вращающий момент на шестерне, Н*мм,

или

отсюда:

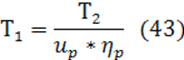
 К_н- коэффициент расчетной нагрузки, К=1,1…..1,20

        a_w – угол зацепления

        α - угол профиля  a_w =α=20˚

        d - диаметр делительной окружности, мм

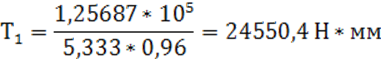
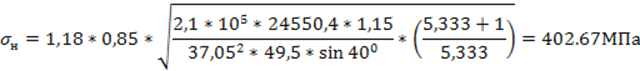
5.4.Определение сил, действующих в зацеплении колес.

При работе агрегата зубчатые пары передают вращающий момент. При этом в зацеплении зубчатых колес возникает нормальная сила F_n, направленная по линии зацепления – общей нормали к рабочим поверхностям зубьев. Эта сила раскладывается по трем взаимно перпендикулярным направлениям. Составляющие этой силы носят названия окружной F_t, радиальной F_r, осевой F_a сил в зависимости от их направления по отношению к оси колеса.

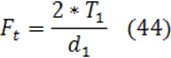
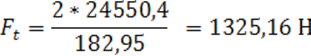
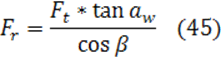
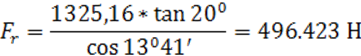
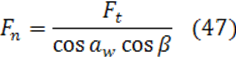
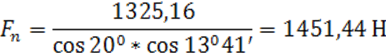
5.5. Проектный расчет валов и предварительный выбор подшипников.

Ориентировочный  размер диаметра быстроходного и тихоходного валов редуктора под соединительную муфту определяется по формуле:

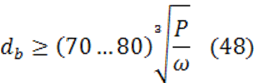
 где: Р – мощность на соответствующем валу, кВт;

 - угловая скорость вала, рад/с

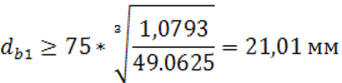
Полученное значение округляем до ближайшего большего из стандартного ряда, принимает:

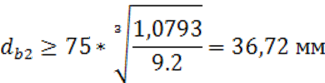
Полученное значение округляем до ближайшего большего из стандартного ряда, принимает:

7Посадочные диаметры валов под подшипники принимаем на 2…5мм,  т.е. 25 и 40 мм соответственно, а посадочные диаметры валов под зубчатые колеса – на 8…10мм больше по сравнению с диаметром под полумуфту.

    Подшипники подбираем по наиболее нагруженной опоре (в которой суммарная радиальная реакция R – наибольшая). На каждой из двух опор вала устанавливают одинаковые подшипники, т.к. F_а˃0,25R  (322,79˃216,99), то выбираем радиально-упорные шарикоподшипники ГОСТ 8338-75.

5.6. Определение реакции опор валов редуктора и подбор подшипников.

Для определения реакции опор А и Всоставляется расчётная схема вала, где реальный вал рассматривается как шарнирно опёртая балка,  к которой приложены силы, действующие в зацеплении зубчатых колёс. Строим расчётную схему, освобождаясь от связей на ней, показываем реакции в опорах. Одна из опор вала (опора А) является шарнирно-неподвижной, а опора В – шарнирно-подвижной. Также покажем радиальные реакции R_AY, R_AZ, R_BY и R_BZ и осевую реакцию R_AX. Размеры l и a определяются по эскизной компоновке редуктора, l=94,5 мм, a=47,25 мм. При этом радиальные опорные реакции считаются приложенными в точках пересечения плоскостей, а силы в зацеплении считаются приложенными на диаметре делительной окружности посредине ширины колеса.

Реакции опор в двух взаимно перпендикулярных направлениях