Гидравлика. Гидродинамика: Сборник типовых задач (краткие сведения из теории, примеры решения задач и задания для выполнения расчетно-графических работ по разделу курса гидравлики «Гидродинамика»)

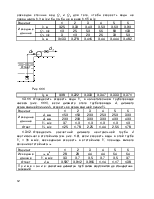
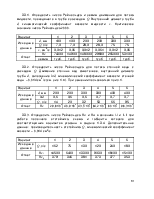
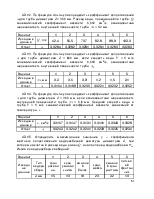
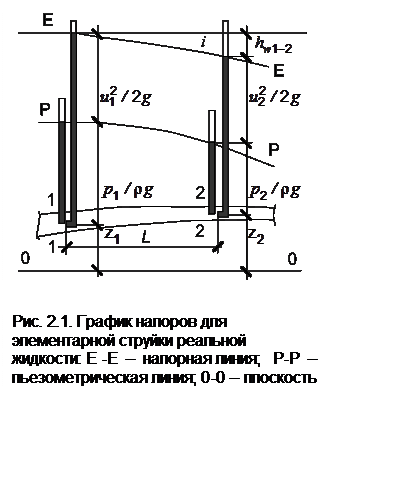
Линию P–P, проведенную по уровням жидкости в пьезометрах, называют пьезометрической. Линия Е–Е, соединяющая отметки гидродинамических напоров вдоль движения, называется напорной.

Каждое из слагаемых уравнения (2.2) с энергетической точки зрения представляет собой разновидность удельной механической энергии, т. е. энергии, отнесенной к единице веса жидкости. Сумма 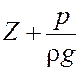 – удельная потенциальная энергия жидкости, а слагаемое  – удельная кинетическая энергия жидкости.

Из уравнения (2.1) следует, что полная удельная механическая энергия элементарной струйки идеальной жидкости остается постоянной в любом сечении.

Для элементарной струйки реальной (вязкой) жидкости уравнение (2.1) принимает вид

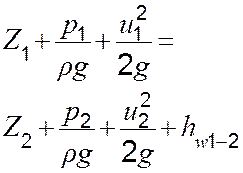,      (2.3)

где  – потери полного напора (полной удельной механической энергии) на преодоление работы сил внутреннего трения, обусловленных вязкостью жидкости.

Если от точки напорной линии, соответствующей гидродинамическому напору в сечении 1–1 (рис. 2.1), провести горизонтальную прямую, вертикальное расстояние от этой прямой до напорной линии в сечении 2–2 определит величину потерь напора.

Полная удельная механическая энергия элементарной струйки реальной жидкости убывает по направлению движения.

Для потока реальной (обладающей вязкостью) жидкости уравнение
Д. Бернулли записывают в виде

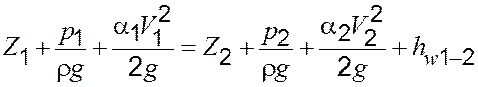,                  (2.4)

где  и  – средние скорости потока движущейся жидкости в рассматриваемых сечениях;  и  – коэффициенты Кориолиса (коррективы кинетической энергии), учитывающие неравномерность распределения местных скоростей по живому сечению потока жидкости. При турбулентном режиме движения a = 1,05–1,15, а для ламинарного режима a = 2,0.

Для потока реальной жидкости уравнение Д. Бернулли является уравнением баланса энергии с учетом ее потерь. Заметим, что теряемая энергия не исчезает бесследно, а лишь превращается в другую форму (тепловую), т. е. теряется потоком безвозвратно.

Потери напора , отнесенные к единице длины, представляют собой гидравлический уклон

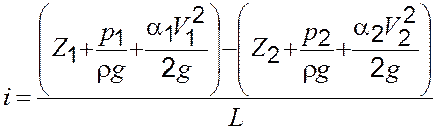,                       (2.5)

где  – гидравлический уклон;  – расстояние между сечениями 1–1 и 2–2 (см. рис. 2.1).

Величина  всегда положительна, так как кривая скоростного напора всегда снижается по направлению потока. Зная гидравлический уклон из справочной литературы (например, из таблиц Ф.А. и А.Ф. Шевелевых), потери напора можно определить по формуле

.                                               (2.6)

В данном разделе для упрощения расчетов используется следующая зависимость

h_w = SQ²,                                             (2.7)

где S – гидравлическое сопротивление трубопровода, с²/м⁵,

S = AL,                                               (2.8)

где  – удельное сопротивление трубопровода, с²/м⁶; Q – расход, м³/с.

Более подробно вопрос определения потерь напора, в том числе для использования в уравнении Бернулли, рассмотрен в подразд. 4.1.

Условия применимости уравнения Бернулли следующие:

• движение установившееся, из массовых сил действует только сила тяжести;

• сечения берутся только там, где поток параллельноструйчатый или плавно изменяющийся. При этом совсем не обязательно, чтобы поток на всем участке между рассматриваемыми сечениями был близким к параллельноструйчатому;

• для сжимаемой жидкости движение должно происходить при постоянном давлении и температуре без разрывов струй и образований пустот;

• сечения потока плоские и перпендикулярны векторам скорости.

Уравнение Бернулли удобно применять, следуя схеме:

1) устанавливаем два сечения, которые будем соединять уравнением Бернулли. Здесь надо отмечать такие сечения, для которых известно возможно большее число гидродинамических элементов. Если потребуется найти тот или другой  гидродинамический элемент для какого-либо живого сечения, то это живое сечение должно быть включено в число двух сечений, соединяемых уравнением Бернулли;

2) намечаем горизонтальную плоскость сравнения. Часто эту плоскость удобно назначать так, чтобы  или , входящее в уравнение Бернулли, обратилось в нуль;

3) пишем уравнение Бернулли в полном виде по формуле (2.4);

4) устанавливаем значения отдельных слагаемых, входящих в это уравнение. При этом следует помнить, что скоростью движения жидкости в резервуаре обычно пренебрегают ввиду ее малости и несопоставимости