Решение модельных задач гидродинамики методом естественных соседей

фиксировано отношение соседства между точками, в отличие от регулярных сеток. В результате, при расчете задач с большими деформациями на такой сетке не возникает явления перехлеста ячеек. Кроме того, к достоинствам диаграммы Вороного следует отнести выпуклость ячеек и гладкую зависимость ячеек от координат узловых точек.

Построение диаграммы Вороного является нетривиальной задачей, требующей специального рассмотрения. Существуют универсальные индуктивные алгоритмы, позволяющие построить разбиение Вороного для произвольного набора точек в областях не слишком сложной формы. Но такие алгоритмы требуют большого количества операций и, поэтому, неэкономичны при построении разбиения на каждом временном шаге, как того требуют лагранжевы методы. В 1987 году Стивен Фортун предложил алгоритм “sweep plane” (алгоритм “заметающей плоскости”) для вычисления диаграммы Вороного, временная сложность которого составляет  [11]. Идея “sweep plane” методов заключается в перемещении горизонтальной линии “sweep plane” (“линии зачистки") сверху вниз по плоскости. Во время выполнения "зачистки" формируется информация относительно структуры, описывающей диаграмму Вороного.

Дискретизация области ячейками Вороного позволяет осуществлять быстрый поиск естественных соседей для заданной точки. Нахождение естественных координат на основе информации о смежных узлах, полученной из диаграммы Вороного, существенно снижает временные затраты, необходимые для построения интерполирующих функций [5]. Соответственно, скорость работы методов, интерполяции которых основаны на разбиении Вороного (методы NEM и MFEM) зависит от эффективности алгоритма, реализующего разбиение области ячейками Вороного, что особенно актуально при численном решении задач механики жидкости со свободными границами.

1. Общая постановка задачи о течении идеальной жидкости со свободной границей

Ниже приведем общую постановку плоской нестационарной задачи течения идеальной жидкости со свободной границей.

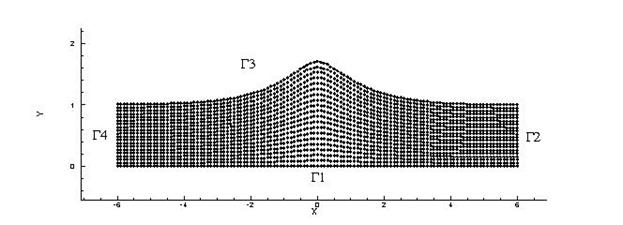
Рисунок 1 - Схема расчетной области

В расчетной области течения , представленной конечным набором узлов, ограниченной свободной поверхностью  и твердыми стенками , выполняется закон сохранения массы (рисунок 1):

.                                                                                                          (1)

Закон движения частиц области  описывается уравнением Эйлера:

,                                                                                                     (2)

В уравнениях (1)–(2)  - вектор скорости и давления частиц жидкости соответственно,  - плотность,  - вектор внешних сил.

На твердых стенках выполняется условие непротекания:

,                                                                                                                      (3)

где  – внешняя нормаль к поверхности жидкости.

На свободной поверхности выполняется условие:

.                                                                                                                    (4)

Так как задача нестационарная, то необходимо задать начальное положение свободной границы  и распределение поля скоростей во всей области течения.

Требуется найти положение свободной поверхности жидкости в последующие моменты времени и поле скоростей в эти моменты времени во всех точках области.

2. Алгоритм движения по времени (схема расщепления)

Интегрирование по времени системы уравнений (1)–(2) представляет некоторые трудности, когда жидкость несжимаемая или слабо сжимаемая. В этом случае, не может быть использован явный метод интегрирования по времени, и даже при использовании