Исходные данные:
· изучаемые моменты или периоды времени- ti;
· изучаемые уровни (показатели ) - Уi .
Определить:
|
· абсолютные приросты |
DУ i; |
|
· темп роста |
К i; |
|
· темп прироста |
DК i; |
|
· средний уровень ряда |
У ср ; |
|
· средний абсолютный прирост |
DУ ср; |
|
· средний темп роста |
К ср; |
|
· средний темп прироста |
DК ср. |
К основным показателям динамики относятся:
1. Абсолютный прирост (цепной и базисный);
2. Темпы роста (цепные и базисные);
3. Темпы прироста (цепные и базисные).
Для более наглядного представления базисных и цепных показателей воспользуемся их графическими представлениями в обобщенном виде.
 Базисные показатели
Базисные показатели
Цепные показатели.
Абсолютный прирост - сравнение (разность) текущего уровня ряда с предыдущим (цепной), либо с базисным (базисный прирост)
D ц = Yi ‑ Yi-1 цепной абсолютный прирост.
D б = Yi ‑ Y1 базисный абсолютный прирост.
Темпы роста - соотношение (деление) текущего уровня к предшествующему, либо к базисному.
Kiц =( Yi / Yi-1 ) *100 цепные темпы роста (в процентах).
Kiб =( Yi /Y1 )*100 базисный темп роста (в процентах).
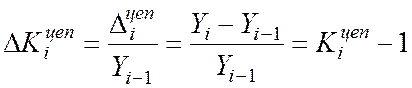 |
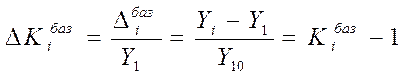 |
На практике часто происходит сравнение показателей динамики по нескольким показателям. Например, сравнение темпов роста цен и темпов роста производства товаров и услуг; темпов роста оплаты труда и производительности труда.
Расчет показателей динамики достаточно трудоемок, поэтому они считаются по наиболее существенным признакам, при этом используется более высокий уровень обобщения.
Например, в разрезе периодов считается система динамических средних.
Кроме основных показателей, рассчитываются средние величины. К ним относятся:
· средний уровень ряда;
· средний абсолютный прирост;
· средний темп роста;
· средний темп прироста.
Средний уровень ряда рассчитывается с учетом двух условий:
· Вид ряда.
· Вид показателя, по которому построены уровни.
Средние уровни ряда различают для моментного и интервального ряда и рассчитываются по разному для абсолютных и для относительных величин.
Интервальный ряд
Средний уровень интервального ряда по абсолютным величинам (рассчитывается по формуле средней арифметической для несгруппированного ряда):
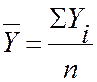 |
n - число учтенных уровней.
Средний уровень интервального ряда по относительным и средним величинам (рассчитывается по формуле средней арифметической для сгруппированного ряда):
![]()
![]()
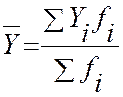
Mоментный ряд. Средний уровень моментного динамического ряда рассчитывается по разным формулам для случаев неравноотстоящих дат и для рядов с равными промежутками времени.
1. Для моментного ряда с неравностоящими датами средний уровень определяется как средняя взвешенная. В качестве веса принимается промежуток времени, в течение которого сохраняется определенный уровень.
По абсолютным величинам:
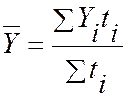
где ti- отрезок времени, в течение которого сохраняется уровень Yiот момента ti до следующего момента.
По относительным величинам:
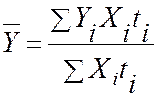
2. Моментный динамический ряд с равными промежутками времени (рассчитывается по формуле средней хронологической).
а) по абсолютным величинам
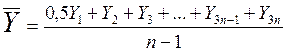
где n - число учтенных уровней/
Cредний абсолютный прирост рассчитывается по формуле простой арифметическойнезависимо от вида показателя. При этом учитывается наличие данных за предыдущий период.
В том случае, когда известен конечный уровень предыдущего периода, средний абсолютный прирост для изучаемого отрезка времени равен:
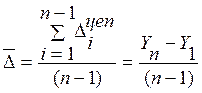
где Yn - конечный уровень изучаемого периода,
Y1 - начальный уровень изучаемого периода,
n - число уровней в изучаемом периоде.
Средний темп роста показывает, во сколько раз в среднем за отдельные составляющие рассматриваемого периода изменялись уровни динамического ряда.
Средний темп роста может быть рассчитан по формуле средней геометрической или через цепные темпы роста.
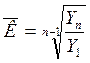 |
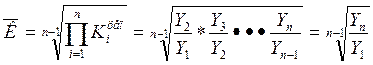 |
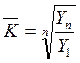 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.