Примеры решения задач по темам части № 2 «Металлы, полупроводники, диэлектрики». Сводка формул

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПО ТЕМАМ ЧАСТИ №2

« МЕТАЛЛЫ, ПОЛУПРОВОДНИКИ, ДИЭЛЕКТРИКИ»

СВОДКА ФОРМУЛ

1. Закон Видемана - Франца

                                                           ,

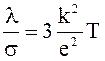где l - коэффициент теплопроводности.

     2. Удельная проводимость собственных полупроводников

                                                   ,

где DЕ - ширина запрещенной зоны, s₀ - константа. С другой стороны

                                                      ,

где u_n  и  u_p - подвижность электронов и дырок.

3.  Удельные проводимости в полупроводниках с донорной и акцепторной проводимостями

                      ,                                 ,

где n и р - концентрация электронов и дырок соответственно.

4.  Постоянная Холла для полупроводников с носителями тока одного типа (n или р)

                                                .

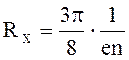5.   Напряжение на гранях образца при эффекте Холла

                                                 ,

где R_x - постоянная Холла, В - магнитная индукция, b - ширина пластины, i - плотность тока.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача1 Исходя из классической теории электропроводности металлов, определить среднюю кинетическую энергию электронов в металле <Е> если отношение коэффициента теплопроводности к удельной проводимости l/s = 6,7 10^-6 В²/К.

Дано: l/s = 6,7 10^-6 В²/К. Найти: <Е> = ?

Решение: По закону Видемана - Франца

                                                            ,

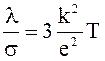откуда найдем абсолютную температуру

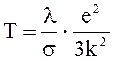                                                            .                                               (1)

Считая, что электронный газ в металле подчиняется классической теории, можно воспользоваться выводами молекулярно-кинетической теории идеального газа. В частности, средняя энергия частиц по этой теории

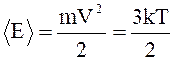                                                     .                                            (2)

Подставим в (2) выражение  (1):

                                                    .

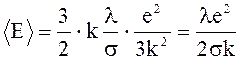Вычислим ответ:

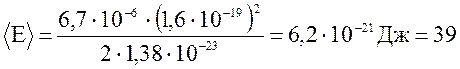                                 МэВ.

Задача 2. Удельная проводимость кремния с акцепторной примесью равна 112 (Ом м)^-1. Определить подвижность дырок и их концентрацию, если постоянная Холла равна 3,66 10^-4 м³/Кл.

Дано: s = 112 (Ом м)^-1; R_X = 3,66 10^-4 м³/Кл. Найти: U_P = ? р = ?

Решение: Удельная проводимость полупроводника с дырочной проводимостью определяется по формуле

                                                   ,

где е - заряд электрона, р - концентрация дырок, u_Р - подвижность дырок.

Концентрацию дырок находим из формулы, определяющей постоянную Холла:

                                                      .

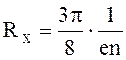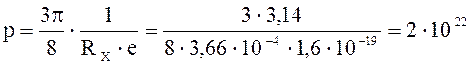                                   м^-3.

Подвижность дырок

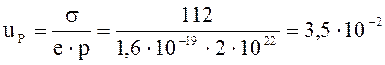                                    м²/(В с).

Задача3. Сопротивление полупроводникового кристалла PbS при температуре 20 ⁰С равно 10⁴ Ом. Определить его сопротивление при 80 ⁰С. Ширина запрещенной зоны равна 0,6 эВ.

Дано: R₁ = 10⁴ Ом; Т₁ = 293 К; Т₂ = 353 К; DЕ = 0,6 эВ = 0,96 10^-19 Дж. Найти : R₂ = ?

Решение: Удельная проводимость собственных полупроводников может быть определена по формуле

                                            ,

с учетом которой удельное сопротивление r и сопротивление R могут быть рассчитаны по соответствующим формулам:

                          ;                  .

Для температур Т₁ и Т₂ имеем

                       и              .

Поделив R₂ на R₁ , получим

                                                .

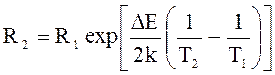Подставим числовые значения:

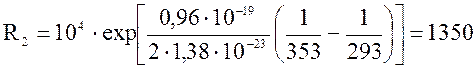                                  Ом.