Решение задач линейного программирования. Решение целочисленной задачи методом Гомори

Типовой расчет

Задание 1. Решить задачу линейного программирования:  a) графически, b) симплекс-методом.

Задание 2. Решить задачу линейного программирования  симплекс-методом.

Задание 3. Решить задачу линейного программирования симплекс-методом, составить двойственную задачу и найти ее решение.

Задание 4. Решить целочисленную задачу методом Гомори.

Задание 5. Решить транспортную задачу.

Задание 6. Дана платежная матрица игры. Найти седловые точки и оптимальные стратегии игроков.

Задание 7. Дана платежная матрица игры. Решить графически игру.

Задание 8. Дана платежная матрица игры. Найти решение  игры путем сведения ее к задаче линейного программирования.

Примеры решения  заданий

Задачи линейного программирования

Пример 1. Решить ЗЛП                  f(x) = 3x₁ + 2x₂ ® max

x₁ + x₂ £ 4,

 2x₁ + x₂ £ 6,

   x₁ ³ 0, x₂ ³ 0,

a) графически,  b) симплекс-методом.

a) Шаг 1. Строится множество D допустимых решений  задачи, оно представляет собой  четырехугольник ОABC на плоскости x₁О x₂ с вершинами в точках О, А, В, С,  с координатами (0; 0), (0; 4), (2; 2), (3; 0), соответственно.

Шаг 2. Из начала координат откладывается вектор-градиент функции f(x), указывающий направления ее возрастания.

Шаг 5.Находится оптимальное значение функции.

f ^*(2; 2) =3x₁ + 2x₂ = 3 × 2 + 2 × 2 = 10.

b) Шаг 1. Задача приводится к специальному виду, для этого к левым частям неравенств прибавляются дополнительные переменные x₃ и x₄, превращающие неравенства в равенства.

         f(x) =3x₁ + 2x₂ ® max

x₁ + x₂ + x₃ = 4,

2x₁+ x₂ + x₄ = 6,

    x_j ³ 0,

Переменные x₃ и x₄ входят в первое и второе уравнения соответственно с коэффициентами единица, тогда х₃ , х₄  – начальный базис,  x₁ , x₂  – свободные переменные, b  – вектор ограничений.

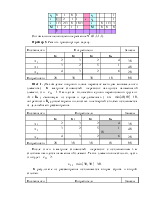
   Шаг 2. Составляется соответствующая симплекс - таблица:

Так как свободные переменные всегда равны нулю, то для данного начального базиса f(x) будет равна нулю:

f(x) = с₀ - åc_i х_i = 0 × 2 + 0 × 6 = 0.

Так как имеются с_j < 0, приступаем к улучшению плана.

   Шаг 3. Выбирается разрешающий j-й столбец, соответствующий наименьшему отрицательному с_j.

         Шаг 4. Разрешающую строку определяют следующим образом: рассчитываются так называемые симплексные отношения, т. е. отношения текущих значений базисных переменных к положительным  коэффициентам разрешающего столбца, соответствующим данным базисным переменным. Затем берется минимальное из этих отношений и по тому, какой строке оно соответствует, определяется ведущая строка.

         Шаг 5.  Находится разрешающий элемент, он расположен на пересечении разрешающей строки и разрешающего столбца (в нашем случае он равен 2).

         Шаг 6.  Определяются переменные, которые будут исключены из базиса и включены в него. Переменную, которой соответствует разрешающий столбец, включаются в базис вместо переменной, которой соответствует разрешающая строка.  В базис вводим переменную x₁, которому соответствует минимальное значение c_j. Из базиса выводится x₄, так как минимальное q достигается в этой строке формулой  .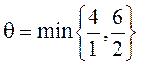

 Таким образом, элемент a₄₁ будет разрешающим (в таблице выделен серым цветом).

Шаг 7. Заполняем таблицу, соответствующую новому базисному решению.

 Шаг 8.  Так как в строке f(x) оценок полученного нового плана имеется отрицательное значение с_j , приступаем к следующей итерации, продолжая улучшать план.

  Поскольку все с_j ³ 0, то план, представленный в данной таблице, будет оптимальным.

Ответ:  f ^*(x) =10; x₁^* = 0; x₂^*= 6

Пример 2.  Решить каноническую задачу линейного программирования:

         f(Х) = х₁ - 2х₂ - 2x₃ ® max

                                                      x₁ + 4x₂ + x₃ = 5,

                                                      x₁ - 2x₂ - x₃ = -1,          

                                                       x_j ³ 0,

Данная каноническая задача линейного программирования (КЗЛП) не является специальной (СЗЛП), поэтому применяем метод искусственного базиса.  Строим вспомогательную задачу линейного программирования и приводим ее к специальному виду,  выражая целевую функцию через небазисные переменныеx_j ,  j=1,…,3. Эта задача имеет вид:

h(Х) = – ( t₁+ t₂) =  – 6 + 6 x₂ + 2 x₃ ® max

                                x₁ + 4x₂ + x₃ + t₁ = 5,

 x₁ - 2x₂ - x₃ + t₂ = -1,

                                                       все  x_j  ≥ 0, t_i  ≥ 0.

Решаем специальную задачу линейного программирования симплекс-методом:

Так как max h = 0, то множество Х допустимых решений КЗЛП не пусто, т. е.

Х ¹ Æ, поэтому существует СЗЛП, эквивалентная данной КЗЛП. Эта задача имеет вид:f(Х) = - 4 + 3х₂ ® max            

 x₁ + x₂  = 2,

 3x₂ + x₃ = 3,

                                                         все  x_j  ≥ 0.

Линейные уравнения этой системы и f(Х)  получены из завершающей симплекс-таблицы вспомогательной задачи.

Решаем специальную задачу линейного программирования симплекс-методом:

Отсюда оптимальный план Х^*(1; 1; 0), f_max = -1.

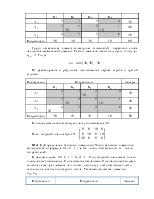
Пример 3. Решить задачу линейного программирования симплекс-методом, составить двойственную задачу и найти ее решение.

            Z = 6x₁ + 5 x₂ + 4x₃ + 3x₄ ® max

2x₁+ 3x₂ + 2x₃ + x₄ £ 25,

4x₁ + x₂ + 3x₃ + 2x₄ £ 30,

  3x₁ +5 x₂ + 2x₃ + 2x₄ £ 42,

                                                    все  x_j  ≥ 0.

Х*(6.5, 4, 0, 0),    Z*=59.

Решение двойственной  задачи можно найти с помощью второй теоремы двойственности:

 (2x₁+ 3x₂ + 2x₃ + x₄ - 25) у₁ = 0 Þ(2 • 6,5 + 3 • 4 - 25) у₁ = 0 Þ 0 = 0,

(4x₁+ x₂ + 3x₃ + 2x₄ - 30) у₂ = 0 Þ (4 • 6,5 + 4 - 30) у₂ = 0 Þ 0 = 0,

(3x₁ + 5x₂ + 2x₃ + 2x₄ – 42) у₃ = 0 Þ (3 • 6,5 + 5 • 4 - 42) у₃ = 0Þ

Þ -2,5у₃ = 0 Þ у₃ = 0,

(2y₁ + 4y₂ + 3y₃ – 6) х₁ = 0 Þ (2y₁ + 4y₂ + 3y₃ –6) 6,5 = 0 Þ (2y₁ + 4y₂ +3y₃ – 6 = 0),

(3y₁ + y₂ + 5y₃ – 5) х₂ = 0 Þ (3y₁ + y₂ + 5y₃ – 5) 4 = 0 Þ (3y₁ + y₂ + 5y₃ – 5 = 0),

(2y₁ + 3y₂ + 2y₃ – 4) х₃ = 0 Þ (2y₁ + 3y₂ + 2y₃ – 4) 0 = 0 Þ 0 = 0,

(y₁ + 2y₂ + 2y₃ – 3) х₄ = 0 Þ 0 = 0.

Решая систему  у₃ = 0;  2y₁ + 4y₂ + 3y₃ – 6 = 0; 3y₁ + y₂ + 5y₃ – 5 = 0,

находим у₁ = 1,4;  у₂ = 0,8;  у₃ = 0;    f * = 25 • 1,4 + 30 • 0,8 + 42 • 0 = 59.

Пример 4. Решить целочисленную задачу линейного программирования методом Гомори.                                      f(Х) =2х₁+х₂® max            

                                 2x₁ + x₃  =3,

                                                     2х₁+ 3x₂ +x₄ =6,          

                                                      все  x_j  ≥ 0.

Сначала находится решение задачи симплекс-методом.

Х^*_нц (3/2; 1; 0; 0).

Переменная х₁ – дробная. Строим по строке х₁ отсечение:

{1/2} x₃ + {0} x₄ ≥ {3/2}, т. е. x₃  ≥ 1.

Здесь дробная часть числа а находится по формуле {а} = а – [a], где [a] – целая часть числа а.       

{1/2} = 1/2 - 0, {0} = 0, {3/2} = 3/2 – 1 = 1/2.

Из последней таблицы

                     f(Х) =4 - 2/3 х₃ - 1/3 х₄  ® max

                                  1/2 x₃ + x₁  = 3/2,

                                                      -1/3 х₃ + 1/3 x₄ + x₂ =1,         

                                                       все  x_j  ≥ 0.

Составляем задачу с дополнительным ограничением:

      f(Х) =4 - 2/3 х₃ - 1/3 х₄ ® max

                          1/2 x₃ + x₁  = 3/2,

                                              -1/3 х₃ + 1/3 x₄ + x₂ = 1,         

                                               х₃ - х₅ = 1,

                                               все  x_j  ≥ 0.

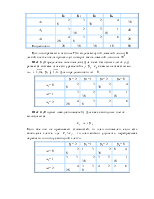
Полученную задачу решаем М-методом:

F(X) = 4 - 2/3 х₃ - 1/3 х₄ – M t₁ = 4 - 2/3 х₃ - 1/3 х₄ + M (-1 + x₃ - x₅) ® max

                          1/2 x₃ + x₁  = 3/2,

                                              -1/3 х₃ + 1/3 x₄ + x₂ = 1,         

                                               х₃ - х₅ + t₁ = 1,

                                               t₁ ≥ 0, все  x_j  ≥ 0.

х₂ = 4/3, требуется еще итерация. Из последней симплекс-таблицы

        f(Х) =10/3 - 1/3 х₄ - 2/3 x₅ ® max

                                                 х₁ + 1/2 х₅ = 1,

 х₂ + 1/3 х₄  - 1/3 х₅ = 4/3,

                                                 - х₅ + х₃ = 1,

                                                {1/3} х₄ + {-1/3} х₅  ≥ {4/3},

                                                 все  x_j  ≥ 0.

{-1/3} = - 1/3 – (-1) = 2/3, {4/3} = 4/3 – 1 = 1/3.

Получаем каноническую задачу линейного программирования :

        f(Х) =10/3 - 1/3 х₄ - 2/3 x₅ ® max

                                                 х₁ + 1/2 х₅ = 1,

 х₂ + 1/3 х₄  - 1/3 х₅ = 4/3,

                                                 - х₅ + х₃ = 1,

                                                 х₄ + 2х₅ - х₆ = 1,

                                                 все  x_j  ≥ 0.

Применяем М-метод.

                                F(Х) =10/3 -1/3 х₄ - 2/3 x₅ – M (1 - (х₄ + 2х₅  - х₆)) ® max

х₁ + 1/2 х₅ = 1;    х₂ + 1/3 х₄  - 1/3 х₅ = 4/3;  - х₅ + х₃ = 1;    х₄ + 2х₅ - х₆ + t = 1;

                                                 t ≥ 0, все  x_j  ≥ 0.

Оптимальное целочисленное решение Х^*_ц (1,1,1,1).

Пример 5. Решить транспортную задачу.

Шаг 1. (Нахождение опорного плана перевозок методом минимального элемента.)  В  матрице стоимостей  перевозок находится наименьший элемент, это    Находится  количество единиц перевозимого груза