































число степеней свободы определяется способом нахождения ![]() , точнее способом нахождения
, точнее способом нахождения ![]() .
.
Лучшим способом является нахождение ![]() по параллельным опытам (опытам,
поставленным в одной точке). В этом случае
по параллельным опытам (опытам,
поставленным в одной точке). В этом случае
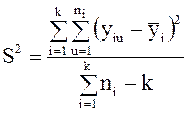 , (9)
, (9)
где
![]() -
- ![]() -е
значение
-е
значение ![]() в точке
в точке ![]() ,
, ![]() – число повторных наблюдений в точке
– число повторных наблюдений в точке ![]() ,
, ![]() - число
точек, в которых проводятся повторные опыты.
- число
точек, в которых проводятся повторные опыты.
Тогда величина 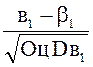 имеет
имеет ![]() -распределение с
-распределение с 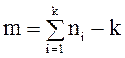 степенями
свободы. Доверительный интервал для
степенями
свободы. Доверительный интервал для ![]() , соответствующий
доверительной вероятности
, соответствующий
доверительной вероятности ![]() , имеет вид
, имеет вид
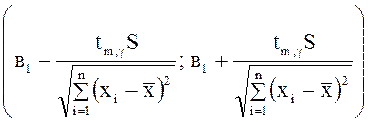 ,
,
где
![]() - значение
- значение ![]() , при
котором
, при
котором ![]() .
.
Замечание. Если параллельных опытов нет, то оценка ![]() может быть найдена следующим образом.
Пусть
может быть найдена следующим образом.
Пусть ![]() - предсказанное значение
- предсказанное значение ![]() данного
данного ![]() , когда
, когда ![]() определены, т. е.
определены, т. е. ![]() .
.
В качестве оценки ![]() может
быть принято следующее отношение:
может
быть принято следующее отношение:
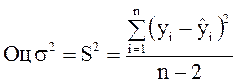 . (10)
. (10)
Сумма 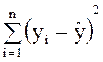 имеет
имеет ![]() степени свободы, т. к. по данным испытаний
определяются два коэффициента. Величина
степени свободы, т. к. по данным испытаний
определяются два коэффициента. Величина 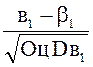 в
этом случае имеет
в
этом случае имеет ![]() -распределение с
-распределение с ![]() степенями свободы.
степенями свободы.
Доверительный интервал для ![]() можно
использовать для проверки гипотезы
можно
использовать для проверки гипотезы ![]() . Если доверительный
интервал, соответствующий доверительной вероятности
. Если доверительный
интервал, соответствующий доверительной вероятности ![]() ,
содержит значение
,
содержит значение ![]() , то гипотеза
, то гипотеза ![]() не отвергается на уровне значимости
не отвергается на уровне значимости ![]() . В частности доверительный интервал может
быть использован для проверки гипотезы
. В частности доверительный интервал может
быть использован для проверки гипотезы ![]() . Если
гипотеза
. Если
гипотеза ![]() отвергается, то параметр
отвергается, то параметр ![]() называется значимым. Аналогичными
рассуждениями можно получить доверительный интервал для
называется значимым. Аналогичными
рассуждениями можно получить доверительный интервал для ![]()
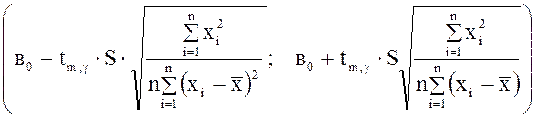 ,
,
где
![]() определяется способом нахождения
определяется способом нахождения ![]() .
.
Интерес для практики представляет доверительный
интервал для линии регрессии. Для его построения необходимо знать оценку
дисперсии ![]() .
. 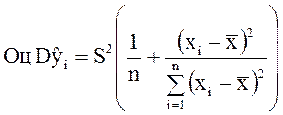 , где
, где
![]() определяется по формуле (9) или (10).
определяется по формуле (9) или (10).
Доверительный интервал для ![]() имеет
вид
имеет
вид
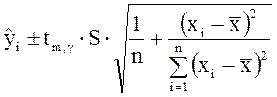 . (11)
. (11)
Доверительная зона (11) определяет местоположение линии регрессии, а не воз-
можных
значений зависимой переменной. Доверительный интервал для значений ![]() определяется по формулам
определяется по формулам
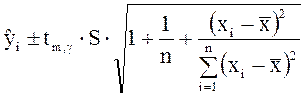 .
.
Проверка модели на адекватность
Проверить модель на адекватность можно сравнивая ![]() -дисперсию, характеризующую разброс
значений
-дисперсию, характеризующую разброс
значений ![]() около линии регрессии (10), и
около линии регрессии (10), и ![]() – дисперсию, характеризующую ошибку опыта
(9).
– дисперсию, характеризующую ошибку опыта
(9).
Для проверки используется отношение 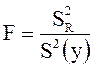 , имеющее в случае адекватности модели
, имеющее в случае адекватности модели ![]() -распределение с
-распределение с 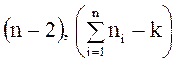 степенями
свободы. Если
степенями
свободы. Если 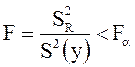 , где
, где ![]() -
критическое значение, соответствующее уровню значимости
-
критическое значение, соответствующее уровню значимости ![]() ,
то нет оснований сомневаться в адекватности модели. В этом случае
,
то нет оснований сомневаться в адекватности модели. В этом случае ![]()
так
же, как и ![]() , может служить оценкой неизвестной
, может служить оценкой неизвестной ![]() . Если же
. Если же 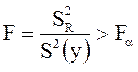 , то
гипотеза об адекватности модели отвергается на уровне значимости
, то
гипотеза об адекватности модели отвергается на уровне значимости ![]() .
.
Замечание 1.
Проверить модель на адекватность можно, расщепляя сумму квадратов 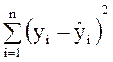 на сумму квадратов, связанную с чистой
ошибкой опыта, и на сумму квадратов, связанную с неадекватностью.
на сумму квадратов, связанную с чистой
ошибкой опыта, и на сумму квадратов, связанную с неадекватностью.
|
относительно регрессии с
|
степенями свободы. |
|
Отношение
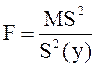 имеет
имеет ![]() -распределение
с
-распределение
с ![]() ,
, ![]() степенями
свободы,
степенями
свободы,
если модель корректна. Критическая область выбирается аналогично предыдущему варианту.
Замечание 2.
Если нет возможности оценить чистую ошибку опыта по параллельным опытам, то
проверить модель на адекватность можно следующим образом. Построить линейную
модель первого порядка и найти остаточную сумму квадратов 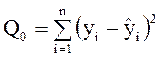 с числом степеней свободы
с числом степеней свободы ![]() . Затем построить линейную зависимость
второго порядка и найти остаточную сумму квадратов
. Затем построить линейную зависимость
второго порядка и найти остаточную сумму квадратов 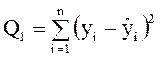 с
числом степеней свободы
с
числом степеней свободы ![]() . Тогда сумма квадратов
. Тогда сумма квадратов ![]() будет иметь
будет иметь ![]() степень
свободы. В качестве критерия проверки гипотезы об адекватности рассматривается отношение
степень
свободы. В качестве критерия проверки гипотезы об адекватности рассматривается отношение
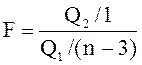 ,
,
имеющее
![]() -распределение с
-распределение с ![]() ,
,
![]() степенями свободы, если справедлива
степенями свободы, если справедлива
гипотеза о несущественности криволинейности.
Заключение
При использовании аппарата математической статистики, в частности регрессионного анализа, надо иметь ввиду, что, во-первых, никакие статистические методы не улучшают плохих наблюдений и, во-вторых, глубоко ошибочным является весьма распространенное убеждение о том, что в результате статистической обработки данных выводится функциональная зависимость.
Интерпретация полученного уравнения регрессии во многом зависит от априорных знаний о специфике явления, для математического описания которого привлечен регрессионный анализ. В связи с этим повышается роль экспериментатора (исследователя), обязанного вникнуть в механизм явления, собрать все сведения о круге факторов, оказывающих влияние
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.