1.03.2010
Моделирование предпочтений
Предпочтение – это одно из фундаментальных понятий ТПР
Формулирование предпочтений является прерогативой ЛПР, свое предпочтение на множестве предъявленных элементов ЛПР может выразить только в отношении какого-то определенного свойства элемента, свойство, которое интересует ЛПР в отношении удовлетворения его потребностей.
Не бывает наилучших решений вообще, каждое решение наилучшее для конкретной задачи, только в конкретных условиях и только для конкретного ЛПР.
Рассмотрим основные способы выявления предпочтений:
1)Ранжирование, заключается в расположении предъявленных элементов в порядке возрастания или убывания их предпочтительности. Прямое ранжирование – ранжирование в порядке возрастания. Обратное ранжирование - ран
При ранжировании каждому элементу в упорядоченном ряду приписывется упорядоченное число, называемое рангом. Т.о. при прямом ранжровании, а при обратном – большее.
Пример
Для формирования приказа о зачислении на 1 курс необходимо осуществить прямое ранжирование 10 абитуриентов по результатам ЕГЭ:
|
Абитуриент |
Результаты ЕГЭ |
Сумма баллов |
Ранг |
||
|
Математика |
Физика |
Русский язык |
|||
|
60 |
54 |
72 |
186 |
9 |
|
|
75 |
65 |
70 |
210 |
6 |
|
|
66 |
52 |
67 |
185 |
10 |
|
|
80 |
74 |
85 |
239 |
2 |
|
|
77 |
65 |
74 |
216 |
5 |
|
|
85 |
81 |
75 |
241 |
1 |
|
|
79 |
68 |
72 |
219 |
||
|
64 |
57 |
77 |
198 |
||
|
67 |
62 |
60 |
189 |
||
|
72 |
71 |
80 |
223 |
||
Ранжирование представляет собой измерение в порядковой шкале, на которую накладываются некоторые требования.
Получаемые в результате ранжирования шкалы должны удовлетворять условию равенства числа ранжируемых элементов общему числу рангов. При строгом ранжировании это условие выполняется автоматически. В обратном случае: величина стандартизированного ранга представляет собой среднее арифметическое суммы мест, поделенных между элементами с одинаковыми рангами.
Пример: Стандартизация рангов
|
Элемент |
Ранг |
Стандартизированный ранг |
|
A |
3 |
(3+4)/2=3,5 |
|
B |
1 |
1 |
|
C |
4 |
(5+6)/2=5,5 |
|
D |
5 |
7 |
|
E |
2 |
2 |
|
F |
3 |
(3+4)/2=3,5 |
|
G |
4 |
(5+6)/2=5,5 |
|
Элемент |
Ранг |
Стандартизированный ранг |
|
A |
2 |
(2+3+4)/3=3 |
|
B |
1 |
1 |
|
C |
3 |
(5+6)/2=5,5 |
|
D |
2 |
(2+3+4)/3=3 |
|
E |
3 |
(5+6)/2=5,5 |
|
F |
2 |
(2+3+4)/3=3 |
|
G |
4 |
7 |
Недостаток ранжирования – малая размерность решаемой задачи.
1)Чтобы
определить место одного из n элементов
среди других, необходимом сопоставить его с остальными (n-1)
элементами, следовательно, для ранжирования всех элементов необходимо выполнить
![]() сравнений.
сравнений.
При большом количестве элементов трудоемкость ранжирования возрастает существенно.
2)Имплицитное сопоставление элементов – сопоставляя элементы, не фиксируем промежуточные данные, поэтому велика вероятность ошибки.
2)По парное сравнение – наиболее выразительный способ выявления предпочтений, результаты которого представляются в виде числовой матрицы, матрицы парных сравнений. В матрице предпочтения могут задаваться без учета и с учетом предпочтений.
По парное сравнение без учета интенсивности предпочтения
Строгое предпочтение:
1)Элемент xi предпочтительнее элемента xj
2)Элемент xj предпочтительнее элемента xi
3)Элементы xj и xi равноценны
Элемент
матрицы формируется: 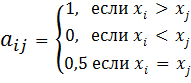
|
Элемент |
A |
B |
C |
D |
E |
|
A |
1 |
1 |
1 |
0 |
1 |
|
B |
0 |
1 |
0 |
0 |
1 |
|
C |
0 |
1 |
1 |
1 |
0 |
|
D |
1 |
1 |
0 |
1 |
1 |
|
E |
0 |
0 |
1 |
0 |
1 |
Нестрогое предпочтение отличается от строгого, тем что оба элемента равноценны
|
Элемент |
A |
B |
C |
D |
E |
|
A |
1 |
1 |
0,5 |
1 |
0 |
|
B |
0 |
1 |
0 |
0,5 |
1 |
|
C |
0,5 |
1 |
1 |
0,5 |
0 |
|
D |
1 |
0,5 |
0,5 |
1 |
1 |
|
E |
0 |
0 |
1 |
0 |
1 |
По парное сравнение элементов с учетом интенсивности предпочтения
Для составления матрицы парных событий необходимо иметь вербальную шкалу интенсивности.
В качестве градаций этой шкалы используются слова естественного языка, характеризующие меру предпочтения. Оперировать вербальными значениями трудно, поэтому вербальным значениям противопоставляются баллы из вербальной шкалы.
Вербальная шкала знаний
|
Вербальная шкала |
Отлично |
Хорошо |
Удовлетворительно |
Неудовлетворительно |
«Хуже некуда» |
|
Балл |
5 |
4 |
3 |
2 |
1 |
Вербальная 9-ти бальная шкала Т. Саати:
|
Вербальная мера превосходства |
Равная важность |
Умеренное превосходство |
Существенное превосходство |
Значительное превосходство |
Очень сильное превосходство |
|
Кратность превосходства |
1 |
3 |
5 |
7 |
9 |
Попарное сравнение с учетом интенсивности предпочтений
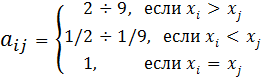
|
Элемент |
A |
B |
C |
|
A |
1 |
1/3 |
5 |
|
B |
3 |
1 |
9 |
|
C |
1/5 |
1/9 |
1 |
Все
остальные элементы рассчитаны по правилу: ![]() ;
; ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.