Неучет остальных элементов множества предъявления при сравнении каждой пары элементов может привести к несовместимости предпочтений. Несовместимость предпочтений проявляется в нетранзитивности бинарных отношений. Для трех элементов А, В, С нетранзитивность предпочтений выражается следующими отношениями предпочтений. A>B, В>C, C>A
В графе недоминирования эта нетранзитивность выражается
циклом: A>B>C>A. Для оценки транзитивности
предпочтений используется коэффициент совместности оценок: ![]() , d- число циклов в
орграфе, определяемое относительно всех троек вершин графа доминирования.
, d- число циклов в
орграфе, определяемое относительно всех троек вершин графа доминирования.
![]()
![]()
![]()
 В
В
А ![]() n(n-1)(2n-1)-
n(n-1)(2n-1)-![]()
![]() - максимальное количество циклов в орграфе:
- максимальное количество циклов в орграфе:
![]() =
=![]() (
(![]()
![]() =
=![]() (
(![]() ,
,
Где n - количество элементов в множестве предъявления;
![]() -оценка предпочтения i-го
элемента над j-м.
-оценка предпочтения i-го
элемента над j-м.
Пример 1:
Требуется найти коэффициент совместности оценок и сделать вывод о транзитивности предпочтений:
|
A |
B |
C |
D |
E |
F |
|
|
|
|
A |
0 |
1 |
1 |
0 |
1 |
1 |
4-приоритет элемента А |
16 |
|
B |
0 |
0 |
0 |
1 |
1 |
0 |
2 |
4 |
|
C |
0 |
1 |
0 |
1 |
1 |
1 |
4 |
16 |
|
D |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
E |
1 |
0 |
0 |
0 |
0 |
1 |
2 |
4 |
|
F |
0 |
1 |
0 |
1 |
0 |
0 |
2 |
4 |
|
Сумма |
- |
45 |
![]() n(n-1)(2n-1)-
n(n-1)(2n-1)-![]() 5-?
5-?
![]() =
=![]() (
(![]() =8
=8
![]() =0,375
=0,375
Вывод: величина коэффициента совместности оценок свидетельствует о неудовлетворительных парных предпочтениях, больше половины которых нарушает требование транзитивности. Для диагностики нетранзитивных предпочтений строится граф предпочтений.
Рисунок))
Циклы: A>B>D>A, A>C>D>A, A>E>C>D, A>F>D>A, B>E>F>B
Противоречивыми являются выделенные предпочтения: A>B>D>A, A>C>D>A, A>E>C>D, A>F>D>A, B>E>F>B
Пример 2
Рассмотрим случай групповых парных сравнений, он предполагает:
1) Получение от экспертов индивидуальных матриц парных сравнений;
2) Совмещение индивидуальных оценок, способ которого зависит от вида предпочтения;
3) Формирование матрицы смежности для групповой матрицы парных сравнений;
4) Расчет коэффициента совместности на основе матрицы смежности.
З эксперта оценили 4 оъекта с применением строгих предпочтений.
|
Э1 |
A |
B |
C |
D |
Э2 |
A |
B |
C |
D |
Э3 |
A |
B |
C |
D |
||
|
A |
1 |
1 |
1 |
1 |
A |
1 |
1 |
1 |
1 |
A |
1 |
0 |
0 |
1 |
||
|
B |
0 |
1 |
1 |
1 |
B |
0 |
1 |
0 |
1 |
B |
1 |
1 |
0 |
0 |
||
|
C |
0 |
0 |
1 |
1 |
C |
0 |
1 |
1 |
0 |
C |
1 |
1 |
1 |
0 |
||
|
D |
0 |
0 |
0 |
1 |
D |
0 |
0 |
1 |
1 |
D |
1 |
1 |
1 |
1 |
Матрица строгих предпочтений имеет следующее свойство: ![]()
![]() отражает факт предпочтения элемента
отражает факт предпочтения элемента ![]()
![]() ,
, ![]()
![]()
В результате можно посчитать число фактов предпочтения ![]()
![]()
![]()
![]() для каждой пары {
для каждой пары {![]()
![]() }. Это свойство дает возможность получать
групповую оценку элементов путем суммирования матриц сформированных тремя
экспертами. Элемент результирующей матрицы
}. Это свойство дает возможность получать
групповую оценку элементов путем суммирования матриц сформированных тремя
экспертами. Элемент результирующей матрицы ![]() перед элементом
перед элементом ![]() и наоборот, т.о. для любой пары элементов {
и наоборот, т.о. для любой пары элементов {![]()
![]() } сумма предпочтений должна быть равна
количеству экспертов, в таком случае мы говорим, что результирующая матрица
корректна.
} сумма предпочтений должна быть равна
количеству экспертов, в таком случае мы говорим, что результирующая матрица
корректна.
![]()
![]()
Результурующая матрица Матрица смежности
|
A |
B |
C |
D |
Э2 |
A |
B |
C |
D |
||
|
A |
3 |
2 |
2 |
3 |
A |
0 |
1 |
1 |
1 |
|
|
B |
1 |
3 |
1 |
2 |
B |
0 |
0 |
0 |
1 |
|
|
C |
1 |
2 |
3 |
1 |
C |
0 |
1 |
0 |
0 |
|
|
D |
0 |
1 |
2 |
3 |
D |
0 |
0 |
1 |
0 |
|
|
Сумма |
12 |
![]() n(n-1)(2n-1)-
n(n-1)(2n-1)-![]() 1
1
![]() =
=![]() (
(![]() =2
=2
![]() =0,5
=0,5
Переход от групповой МПС к матрице смежности осуществляется по правилам:
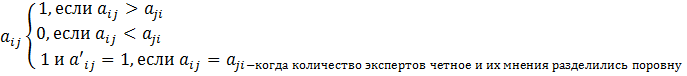
Диагональные элементы групповой МПС в матрице смежности равны 0.
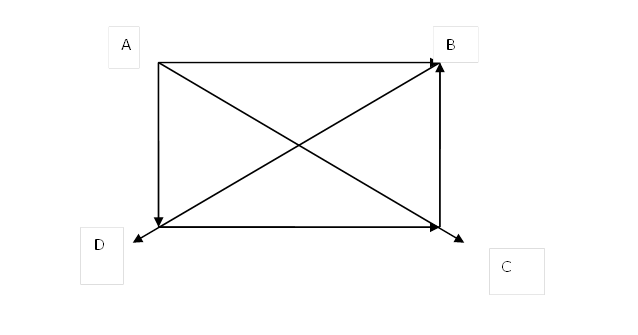
Коэффициент согласия между экспертами: ![]() , где S – общая
степень согласия экспертных оценок:
, где S – общая
степень согласия экспертных оценок: ![]() , i
, i![]() j |(2-1)+(2-1)+(3-0)+(1-2)+(2-1)+(1-2)|=8
j |(2-1)+(2-1)+(3-0)+(1-2)+(2-1)+(1-2)|=8
![]() максимальная согласованность:
максимальная согласованность: ![]() ,
,
где n – количество элементов в множестве предъявления;
![]() оценка предложения i-го
элемента над j-м;
оценка предложения i-го
элемента над j-м;
![]() оценка предложения j-го
элемента над i-м.
оценка предложения j-го
элемента над i-м.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.